Государственное образовательное учреждение дополнительного профессионального образования
«Институт развития образования Кузбасса».
Кафедра естественнонаучного, математического и технологического образования
Подготовка к ОГЭ.
Решение заданий №20.
|
| Исполнитель: |
|
| Пересторонина Ирина Александровна, |
|
| учитель математики МБОУ «СОШ45» г.Кемерово |
|
| +7(950)270 68 15,perestoronina13@mail.ru |
|
| Фазлиахметова Наталья Владимировна |
|
| учитель математики МБОУ «СОШ45» г. Кемерово |
|
| +7 (905) 069 19 77, natali0691977@mail.ru |
|
|
|
|
|
|
|
|
|
|
| Консультант: Трушкина Т.П., ст. преподаватель кафедры естественнонаучного, математического и технологического образования ИРО Кузбасса |
Кемерово 2024
СОДЕРЖАНИЕ
| 1. | Введение | 3 |
| 2. | Характеристика заданий №20 | 4 |
| 3. | Примеры решений алгебраических выражений | 7 |
| 4. | Примеры решений уравнений | 8 |
| 4.1. | Уравнения, решаемые методом введения новой переменной | 8 |
| 4.2. | Уравнения, содержащие квадратные корни | 11 |
| 4.3. | Дробно-рациональные уравнения | 12 |
| 5. | Примеры решений систем уравнений | 14 |
| 5.1. | Способ сложения | 14 |
| 5.2. | Способ подстановки | 16 |
| 6. | Примеры решений неравенств | 17 |
| 6.1. | Квадратичное неравенство | 17 |
| 6.2. | Метод интервалов в решении неравенств | 18 |
| 7. | Примеры решений систем неравенств | 20 |
| 8. | Приложение 1 | 23 |
| 9. | Приложение 2 | 24 |
| 10. | Приложение 3 | 27 |
Введение
Основной государственный экзамен по математике (далее ОГЭ) - одно из важнейших испытаний для школьников. Экзамен требует не только знания математических формул и навыков, но и умения правильно решать задания. Несоблюдение правил оформления может привести к неправильному пониманию задачи и, как следствие, ошибкам в решении. Эти части содержат задания повышенного уровня сложности из различных разделов курса математики. В данном сборнике мы рассмотрим основные правила и рекомендации по решению задания №20 части 2 на ОГЭ по математике.
Задания 2 части направлены на проверку владения материалом на повышенном уровне. Их назначение - дифференцировать хорошо успевающих школьников по уровням подготовки, выявить наиболее подготовленную часть выпускников, как правило в дальнейшем составляющую контингент профильных классов.
Задания 2 части экзаменационной работы носят комплексный характер. Они позволяют проверить владение формально-оперативным аппаратом, способность к интеграции знаний из различных тем школьного курса, владение достаточно широким набором приемов и способов рассуждений, а также умение математически грамотно записать решение.
Требование к выполнению заданий с развернутым ответом заключаются в следующем:
-
решение должно быть математическим грамотным и полным;
-
должен быть понятен ход рассуждений;
-
оформление должно обеспечивать выполнение указанных выше требований.
Важно понимать, что не следует требовать от учащихся слишком подробных комментариев (например, описание алгоритмов). Решение должно быть лаконичным с правильными выкладками, не содержать неверные утверждения.
2.Характеристика задания
Алгебраические выражения:
Во второй части экзамена алгебраическое задание наиболее простое.
В этом номере требуется выполнить одно из предложенных заданий:
Для успешного выполнения данного номера выпускник должен безупречно знать и выполнять тождественные преобразования выражений. Линия тождественных преобразований является одной из четырёх основных содержательных линий школьного курса алгебры (учение о числе, функции, уравнения и неравенства, тождественные преобразования).
Отдельной темой школьного курса математики линия тождественных преобразований не является, она изучается на протяжении всего курса арифметики, алгебры и начал анализа. Начиная с 5-6 классов производятся простейшие тождественные преобразования, которые опираются на законы и свойства арифметических действий. В курсе алгебры основной школы 7-9 классов сконцентрирована основная нагрузка по формированию умений и навыков выполнения тождественных преобразований. Это связано со значительным увеличением числа, а также с разнообразием совершаемых преобразований.
Осуществляется развитие культуры выполнения тождественных преобразований, а также, на основе закрепленных знаний свойств операций и алгоритмов их выполнения развивается культура вычислений. Высокий уровень выполнения тождественных преобразований проявляется в умении правильно обосновать преобразования, в умении проследить за изменением области определения в последовательной цепочке тождественных преобразований, в быстроте и безошибочности выполнения преобразований, в умении найти кратчайший путь решения к окончательному виду преобразований.
В каждой области знаний, которая использует математику, возникает потребность в замене одно выражение другим, для простоты и удобства в решении рассматриваемой задачи. Другими словами, появляется необходимость в выполнении тождественных преобразований.
На уроках математики, в пропедевтическом курсе, начинают отрабатываться навыки тождественных преобразований, такие как:
-
приведение подобных слагаемых;
-
раскрытие и заключение в скобки;
-
вынесение за скобки общего множителя;
-
основное свойство пропорции.
Изучается основное свойство дроби, сокращение дробей, приведение дробей к общему знаменателю, свойство пропорции.
В основной школе, на уроках алгебры, изучаем
-
свойства степени с натуральным и целым показателем;
-
формулы сокращённого умножения;
-
свойства арифметического квадратного корня;
-
способы разложения на множители.
Решение уравнений и систем уравнений задания №20 второй части ОГЭ по математики очень разнообразны и при их решении включают несколько способов, методов решений, которыми учащееся должны владеть:
-
алгоритмами решения линейных, квадратных, дробно-рациональные уравнений и уравнения содержащие квадратные корни;
-
разложением на множители (разные способы);
-
упрощением выражений;
-
свойства квадратного корня;
-
знать формулы дискриминанта и корней квадратного уравнения, теорему Виета
-
способами решения систем уравнений;
-
арифметическими действами над числами.
Все вышеперечисленные умения и навыки учащиеся приобретают в основной школе с 5-9 кассы.
Содержание курса алгебры 7-9 класса:
Уравнения
Понятие уравнения и корня уравнения. Представление о равносильности уравнений. Область определения уравнения (область допустимых значений переменной).
Линейное уравнение и его корни
Решение линейных уравнений. Линейное уравнение с параметром. Количество корней линейного уравнения. Решение линейных уравнений с параметром.
Квадратное уравнение и его корни
Квадратные уравнения. Неполные квадратные уравнения. Дискриминант квадратного уравнения. Формула корней квадратного уравнения. Теорема Виета. Теорема, обратная теореме Виета. Решение квадратных уравнений: использование формулы для нахождения корней, графический метод решения, разложение на множители, подбор корней с использованием теоремы Виета. Количество корней квадратного уравнения в зависимости от его дискриминанта. Биквадратные уравнения. Уравнения, сводимые к линейным и квадратным. Квадратные уравнения с параметром.
Дробно-рациональные уравнения
Решение простейших дробно-линейных уравнений. Решение дробно-рациональных уравнений.
Методы решения уравнений: методы равносильных преобразований, метод замены переменной, графический метод. Использование свойств функций при решении уравнений.
Простейшие иррациональные уравнения вида 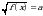 ,
, 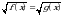 .
.
Уравнения вида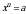 .Уравнения в целых числах.
.Уравнения в целых числах.
Системы уравнений
Уравнение с двумя переменными. Линейное уравнение с двумя переменными. Прямая как графическая интерпретация линейного уравнения с двумя переменными.
Понятие системы уравнений. Решение системы уравнений.
Методы решения систем линейных уравнений с двумя переменными: графический метод, метод сложения, метод подстановки.
Системы линейных уравнений с параметром.
За период обучения с 7-9 класса ученик научится:
-
Решать основные виды рациональных уравнений с одной переменной, системы двух уравнений с двумя переменными.
-
Понимать уравнение как важнейшую математическую модель для описания и изучения разнообразных реальных ситуаций, решать текстовые задачи алгебраическим методом;
-
Применять графические представления для исследования уравнений, исследования и решения систем уравнений с двумя переменными;
Ученик получит возможность:
-
Овладеть специальными приемами решения уравнений и систем уравнений; уверенно применять аппарат уравнений для решения разнообразных задач из математики, смежных предметов, практики;
-
Применять графические представления для исследования уравнений, систем уравнений, содержащие буквенные коэффициенты.
Решение неравенств – это материал, который помогает выявить у экзаменуемого сразу несколько умений и навыков: умения решать уравнения, работать со знаком неравенства, оценить полученное решение с точки зрения постановки неравенства. Поэтому неравенства включены в ОГЭ (ГИА).
Для того чтобы научиться решать задания экзамена ОГЭ, где встречаются линейные неравенства и их системы, следует основательно знать теорию. А именно – основные понятия, обозначения и правила преобразования неравенств.
3. Примеры решения алгебраических выражений.
Рассмотрим несколько видов алгебраических выражений, на которые следует обратить внимание.



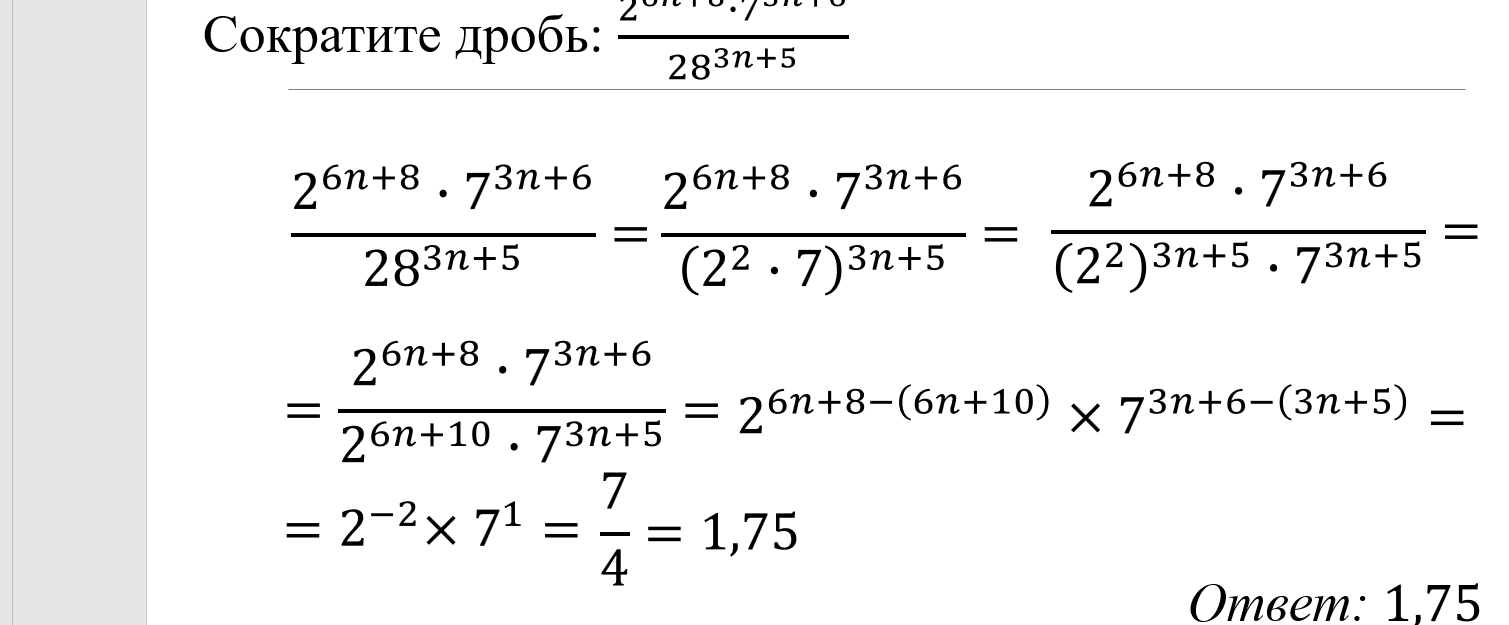


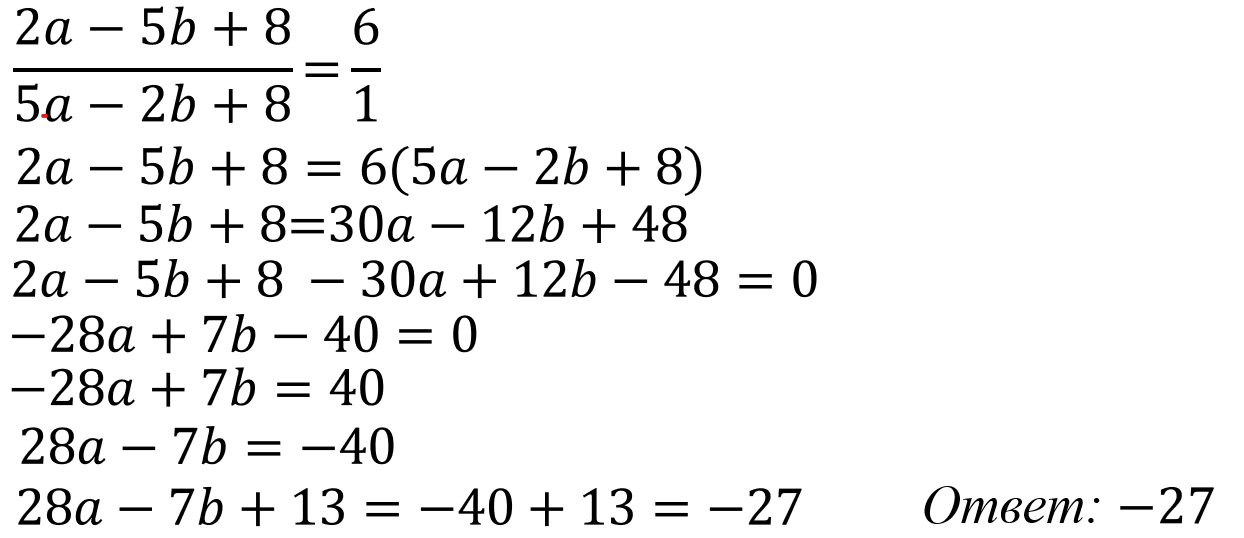
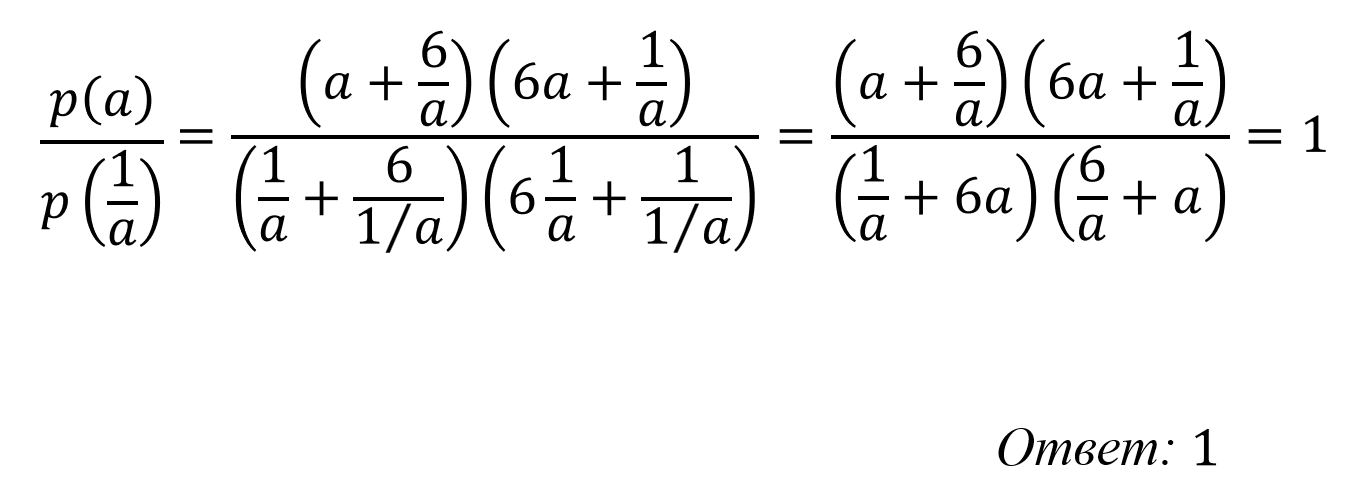
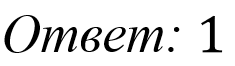
Как тренажёром можно воспользоваться подборкой заданий на сайте https://math100.ru/, алгебраические выражения
4.Примеры решения уравнений
В этом задании могут попасться как легкое линейное уравнение, так и сложное выражение со степенями. Это лотерея, впрочем, как и в остальных заданиях. Но главное здесь твердо оперировать над всеми типами уравнений и уметь упрощать сложные математические выражения.
При разборе решения уравнений 2 части экзаменационной работы необходимо повторить правила, формулы и алгоритмы их решения.
Рассмотрим несколько видов уравнений, на которые следует обратить внимание.
4.1. Уравнения, решаемые методом введения новой переменной
4.1.1. Решите уравнение: 𝑥4 = (4𝑥 − 5)2.
I способ.
Решение. 𝑥4 = (4𝑥 − 5)2.
Перенесем все слагаемые в левую часть и разложим на множители, используя формулу разности квадратов:
𝑥4 − (4𝑥 − 5)2 = 0;
(𝑥2 − (4𝑥 − 5))(𝑥2 + (4𝑥 − 5)) = 0; (𝑥2 − 4𝑥 + 5)(𝑥2 + 4𝑥 − 5) = 0.
Произведение двух множителей равно нулю, если один из множителей равен нулю. Получаем 𝑥2 − 4𝑥 + 5 = 0 или 𝑥2 + 4𝑥 − 5 = 0.
Важно! Употребляется в записи союз «или», а не союз «и». Либо используется запись 𝑥2 − 4𝑥 + 5 = 0; 𝑥2 + 4𝑥 − 5 = 0.
𝑥2 − 4𝑥 + 5 = 0, D = b2 – 4ac = 16 – 20 = – 4, D
𝑥2 + 4𝑥 − 5 = 0, D = b2 – 4ac = 16 + 20 = 36, D 0, уравнение имеет два корня.
Не допустима запись D = 16 + 20 = 36 = √36 = 6. За такую запись в решении уравнения при полученных верных ответах выставляется 0 баллов.
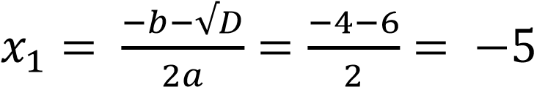 ;
;
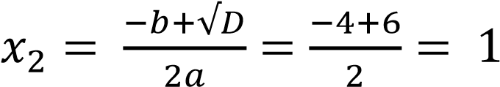 .
.
Ответ: −5; 1.
Важно! В записи ответа используется «−5; 1», не «−5, 1», чтобы не воспринималась десятичная дробь.
II способ.
Решение.
𝑥4 = (4𝑥 − 5)2.
𝑥2 = 4𝑥 − 5; 2 = −4𝑥 + 5.
-
𝑥2 = 4𝑥 − 5,
𝑥 2 − 4𝑥 +4= −1,
(𝑥 − 2)2 = −1, уравнение не имеет корней, так как (𝑥 − 2)2 ≥0 при любых 𝑥.
2)𝑥 2= −4𝑥 + 5;
𝑥 2+4𝑥 + 4=9;
(𝑥 + 2)2 = 9;
𝑥 + 2 = 3;
𝑥 + 2 = − 3;
𝑥 = 1; 𝑥 = − 5.
5.
Ответ: 1; −5.
4.1.2. Решите уравнение: (𝑥 − 2)4 − 6(𝑥 − 2)2 − 7 = 0.
I способ.
Решение.
Пусть (𝑥 − 2)2 = 𝑡, 𝑡 ≥ 0.
Важно! Знак неравенства в данном случае обязательно должен быть нестрогим. Очень часто учащиеся допускают грубую ошибку и теряют полностью баллы за данное задание, указывая 𝑡 0.
Тогда уравнение принимает вид:
𝑡2 − 6𝑡 − 7 = 0,
D = b2 – 4ac = 36 + 28 = 64, D 0, уравнение имеет два корня.
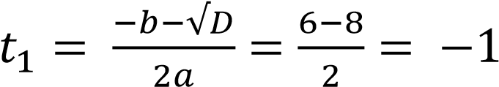 ;
;
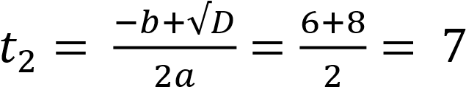 .
.
𝑡 = −1 не удовлетворяет условию 𝑡 ≥ 0,
𝑡 = 7; (𝑥 − 2)2 = 7;
-
𝑥 − 2 = √7;
-
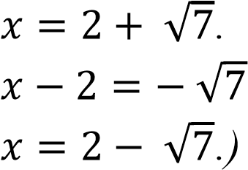 ;
;
Ответ: 2 − √7; 2 + √7.
-
способ.
Решение.
(𝑥 − 2)4 − 6(𝑥 − 2)2 − 7 = 0;
(𝑥 − 2)4 − 6(𝑥 − 2)2 + 9 − 16 = 0;
((𝑥 − 2)2 − 3)2 − 16 = 0;
((𝑥 − 2) − 3 − 4)((𝑥 − 2)2 − 3 + 4) = 0, откуда (𝑥 − 2)𝟐 − 7 = 0 или (𝑥 − 2)𝟐 + 1 = 0.
-
Уравнение (𝑥 − 2)2 = −1 не имеет корней. так как (𝑥 − 2)2 ≥ 0 при любых 𝑥.
-
Уравнение (𝑥 − 2)2 = 7; 𝑥 − 2 = √7 или 𝑥 − 2 = − √7.
𝑥 = 2 + √7 или 𝑥 = 2 − √7.
Ответ: 2 − √7; 2 + √7.
3 способ
Решение.
(𝑥 − 2)4 − 6(𝑥 − 2)2 − 7 = 0; ((𝑥 − 2)2 − 3)2 = 42.
(𝑥 − 2)2 − 3 = 4; (𝑥 − 2)2 − 3 = −4.
-
(𝑥 − 2)2 = 7
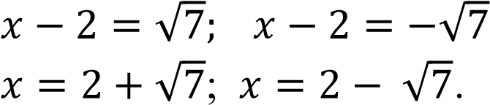 ;
;
-
(𝑥 − 2)2 − 3 = −4;
(𝑥 − 2)2 = −1 уравнение не имеет корней, так как (𝑥 − 2)2 ≥0 при любых 𝑥.
Ответ: 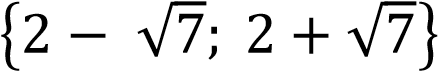 .
.
4.2. Уравнения, содержащие квадратные корни
4.2.1. Решить уравнение: 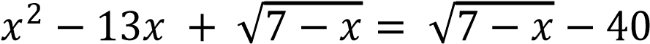 .
.
Важно понимать учащимся, что квадратные корни после преобразований хоть и исчезнут, но в условии они есть. И из определения квадратного корня следует, что подкоренное выражение не может быть отрицательным числом.
Учащиеся часто забывают указать ОДЗ. Но в конце решения все же могут исключить один из получившихся корней, не прописывая при этом условие исключения.
-
способ.
Решение.
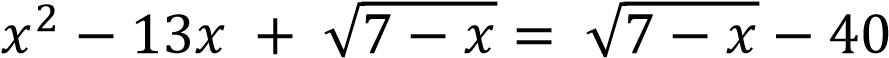 .
.
ОДЗ (область допустимых значений 𝑥)

Откуда 𝑥 = 5 или 𝑥 = 8 − не удовлетворяет ОДЗ.
Ответ. 5.
-
способ.
Решение.
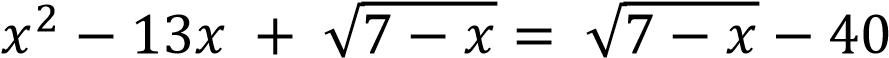 ;
;
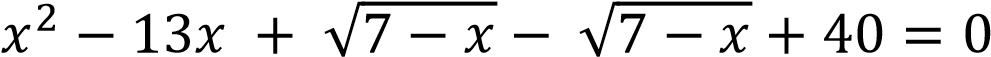
𝑥2 − 13𝑥 + 40 = 0 при условии 7 − 𝑥 ≥ 0, т.е. 𝑥 ≤ 7.
D = (−13)2 − 4 ∙ 1 ∙ 40 = 169 − 160 = 9;
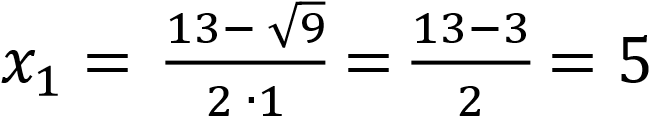 ;
;
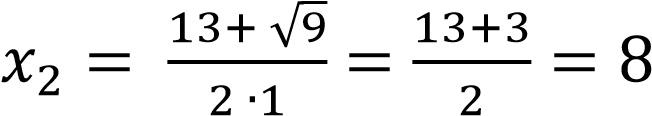 – посторонний корень,
– посторонний корень,
т.к. 𝑥 ≤ 7.
Ответ: 5.
III способ.
Решение.
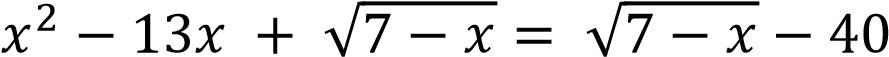 ;
;
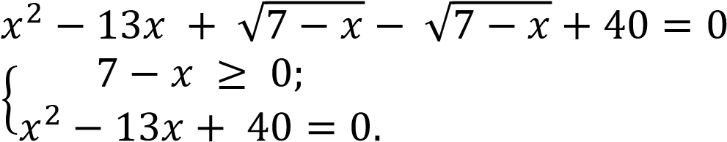 ;
;
D = (−13)2 − 4 ∙ 1 ∙ 40 = 169 − 160 = 9.
𝑥1 = 5;
𝑥2 = 8 – не удовлетворяет условию 7 − 𝑥 ≥ 0.
Ответ: 5.
4.3. Дробно-рациональные уравнения
4.3.1. Решить уравнение: 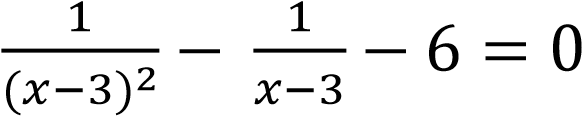 .
.
Решение. Преобразуем левую часть уравнения:
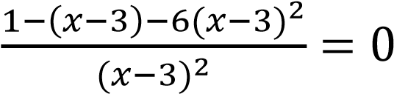 ;
;
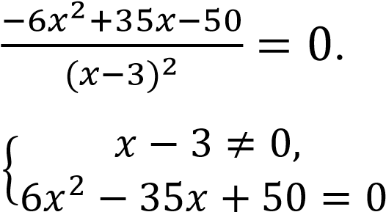
D = (−35)2 − 4 ∙ 6 ∙ 50 = 1225 − 1200 = 25.
 ;
;
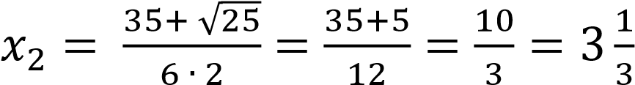 .
.
Оба полученные корня удовлетворяют условию 𝑥 − 3 ≠ 0.
Ответ. 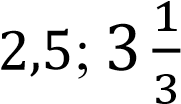 .
.
Важно! В данных уравнениях можно выполнять проверку после нахождения корней. В ходе проверки допускается исключение посторонних корней.
II способ.
Решение.
ОДЗ (область допустимых значений 𝑥):
𝑥 − 3 ≠ 0, т.е. 𝑥 ≠ 3.
Пусть 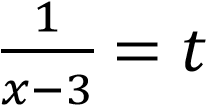 , тогда уравнение принимает вид:
, тогда уравнение принимает вид:
𝑡2 − 𝑡 − 6 = 0. Откуда 𝑡 = −2 или 𝑡 = 3.
Вернемся к переменной 𝑥:
1)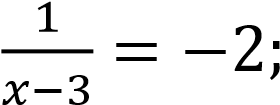 2)
2) 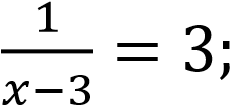
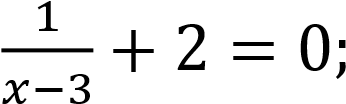
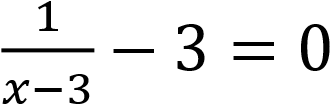
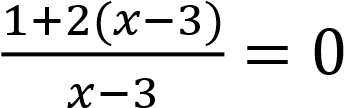 .
. 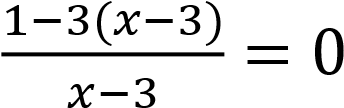 .
.
Учитывая, что 𝑥 − 3 ≠ 0 Учитывая, что 𝑥 − 3 ≠ 0
1 + 2𝑥 − 6 = 0; 1 − 3𝑥 + 9 = 0;
2𝑥 − 5 = 0; −3𝑥 + 10 = 0;
2𝑥 = 5; −3𝑥 = −10;
𝑥 = 2,5; 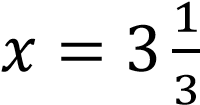 .
.
Оба корня удовлетворяют ОДЗ.
Ответ. 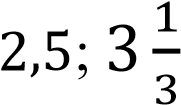 .
.
III способ.
Решение.
Пусть 𝑥 − 3 = 𝑡. Тогда уравнение принимает вид:
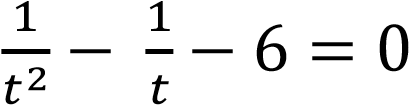 ;
;
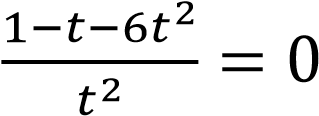 ; ОДЗ: 𝑡 ≠ 0
; ОДЗ: 𝑡 ≠ 0
6𝑡2 + 𝑡 − 1 = 0
D = 12 − 4 ∙ 6 ∙ (−1) = 1 + 24 = 25
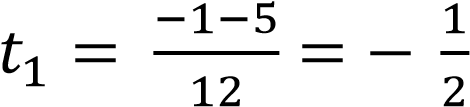 ;
;
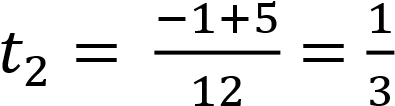 .
.
Так как 𝑥 − 3 = 𝑡, то
-
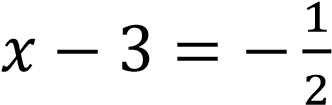 ; 𝑥 = 2,5;
; 𝑥 = 2,5;
-
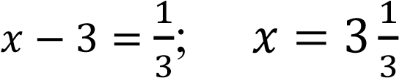 .
.
Ответ. 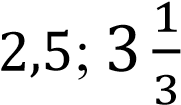 .
.
5.Примеры решения систем уравнений.
Об особенностях оформления решения систем уравнения
На ОГЭ при решении систем уравнений чаще всего используют два основных способа – способ подстановки и способ сложения.
5.1.Способ сложения.
Для способа сложения существует два варианта оформления:
При любом варианте, какой бы не выбрал выпускник, это должно быть сделано грамотно.
5.1.1.Пример решения описательного способа
Решите систему уравнений 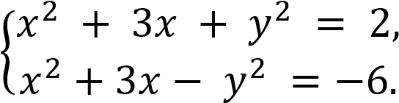
Решение. Используем сложение уравнений данной системы:
2х2 + 6х = - 4 х2 + 3х + 2 = 0
D = 9 - 8 = 1
x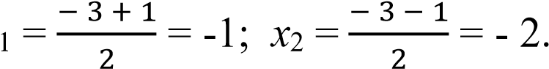
Вычтем из первого уравнения второе, получим:
2y2 = 8 y2 = 4; y = ± 2.
Получим четыре решения системы.
Ответ: (-1; -2), (-1; 2), (-2; -2), (-2; 2).
Важно! Ответ оформлять необходимо именно записью в круглых скобках через точку с запятой, перечисляя через запятую решения системы.
5.1.2.Пример решения методом сложения через равносильные переходы
Решите систему уравнений 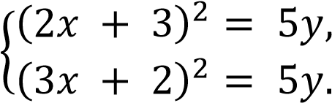
Решение. Вычтем из первого уравнения второе, используем формулу разности квадратов, затем метод подстановки:
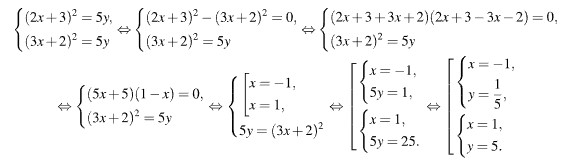
Ответ: (-1; 0,2), (1; 5).
Для ученика 9 класса может оказаться непосильным довести грамотно до конца всю эту конструкцию, поэтому допустимо на каком-то этапе вынести одно из уравнений системы и только потом продолжить решение описательно.
5.2.Способ подстановки.
Для способа подстановки существует два варианта оформления:
5.2.1.Пример решения описательного способа
Решите систему уравнений 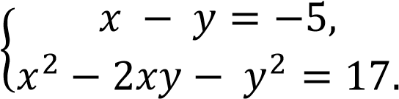
Решение. Выразим переменную y из первого уравнения данной системы: y = x + 5.
Подставим во второе уравнение системы, получим: x2 - 2x(x + 5) - (x + 5)2 = 17
x2 - 2x2 - 10x - x2 - 10x - 25 - 17 = 0
-2x2 - 20x - 42 = 0
x2 + 10x + 21 = 0
D = b2 - 4ac = 100 - 84 = 16 = 42, D 0, уравнение имеет 2 корня,
х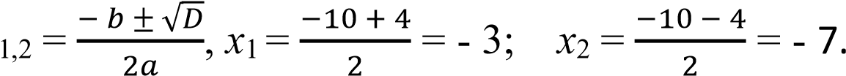
При х = - 3, у = - 3 + 5 = 2.
При х = - 7, у = - 7 + 5 = -2.
Ответ: (-3; 2), (-7; -2).
5.2.2.Пример решения методом сложения через равносильные переходы
Решите систему уравнений 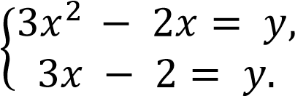
Решение. Последовательно получаем:
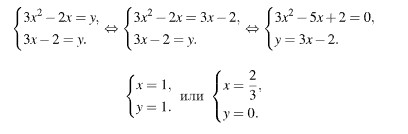
Ответ: (2/3; 0), (1;1).
Важно! В данном решении ученику необходимо прописать решение квадратного уравнения (в данном случае решение способом подстановки довести до системы, где появляется квадратное уравнение. Уравнение вынести отдельно, решить с помощью дискриминанта, найти х и соответствующий ему у).
6. Примеры решений неравенств.
Все неравенства из задачи 20 могут быть разбиты на две группы:
-
квадратичные неравенства,
-
неравенства, которые решаются методом интервалов.
6.1. Квадратичное неравенство (метод параболы)
Важно! Необходимо описать данную функцию, указать, что графиком является парабола. Прописать направление ветвей. Найти нули функции. Схематично изобразить параболу, расставить знаки и записать ответ.
6.1.1. Решить неравенство: 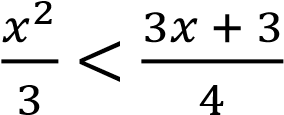
Решение. Решим неравенство, используя метод параболы, для этого сначала преобразуем неравенство.
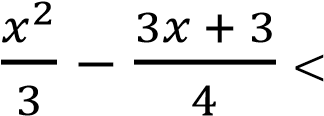 0 | * 120;
0 | * 120;
4х2 - 9х - 9 0.
Рассмотрим функцию у = 4х2 - 9х - 9. Это квадратичная функция, график – парабола, ветви направлены вверх.
Найдем нули функции: 4х2 - 9х - 9 = 0.
D = b2 - 4ac,
D = 92-4* 4*(- 9) = 225 = 152, D 0, уравнение имеет 2 корня,
х 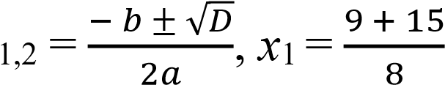 = 3; х
= 3; х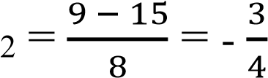 .
.
Изобразим схематично параболу:
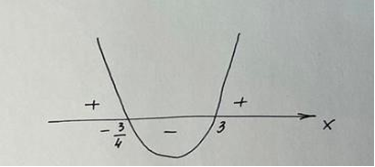
y 0 при х 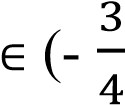 ; 3).
; 3).
Ответ. (- ; 3).
; 3).
6.1.2. Решить неравенство:  ≥ 0
≥ 0
Решение: Так как дробь больше 0, а -18
строго меньше 0, то есть получается неравенство
(х +4)2 – 10
х2 + 8х + 16 – 10
х2 + 8х + 6
Решим неравенство методом параболы
f(х) =х2 + 8х + 6 – квадратичная функция, график – парабола, а = 1 0 = ветви направлены вверх.
Найдем нули функции, т.е. корни уравнения:
х2 + 8х + 6 = 0,
D= 64 – 24 = 40 0, 2 корня
х1 = - 4 + √10
х2 = - 4 - √10
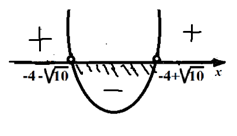
Ответ: х € (-4 - √10; - 4 +√10)
6.2. Метод интервалов в решении неравенств
Важно! В работе необходимо указать, что неравенство решается методом интервалов (написать фразу «решим методом интервалов»). Затем найти корни по всем правилам нахождения корней уравнения (приравнять каждый множитель к нулю), определить знаки выражения на каждом промежутке, нарисовать ось, расставить знаки.
6.2.1. Решить неравенство: (√19 – 4,5) (5 – 3х) 0
Важно! Необходимо прописать правило преобразования, указать, что деление происходит на положительное (отрицательное) число. Прописать действия определения знака разности.
Решение: Определим знак разности √19 – 4,5
Так как 4,5 = √20,25, то √19 √19 - √20,25 √19 – 4,5
При делении на отрицательное число, знак неравенства меняется на противоположный:
(√19 – 4,5)(5 – 3х) 0 / : (√19 – 4,5)
5 – 3х
- 3х

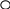
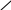



х 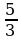
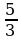
Ответ: ( 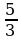 ; +∞ )
; +∞ )
6.2.2. Решить неравенство: (2,5 - √6) (10 – 4х) 0
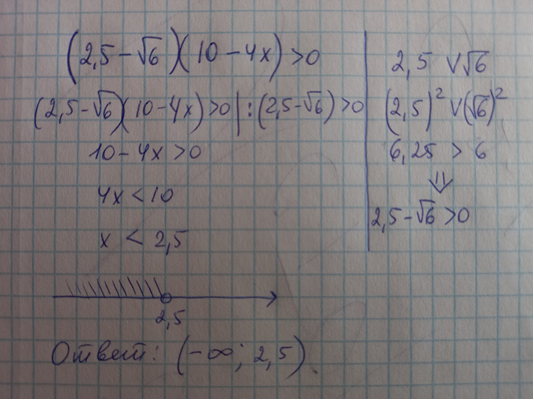
6.2.3. Решить неравенство: (х – 8)
Решение: Преобразуем неравенство.
(х – 8) - √3(х – 8)
(х - 8)(х - 8 - √3) 0.
Решим методом интервалов, для этого найдем корни уравнения:

(х - 8)(х - 8 - √3) = 0,
х - 8 = 0 или х - 8 - √3 = 0, х1 = 8 х2 = 8 + √3.
Определим знаки выражения на каждом промежутке:
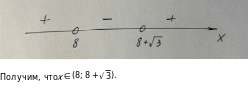
Ответ: (8; 8 + √3).
6.2.4. Решить неравенство: (2 + х)3 ≥ √8 (2 + х)2

6.2.5. Решить неравенство: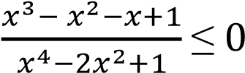
Решение. Данное неравенство является дробным.
Разложим на множители числитель и знаменатель левой части неравенства.
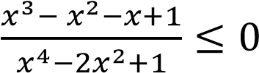 ;
;
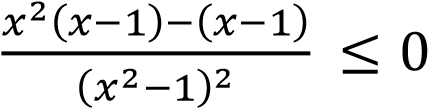 ;
;
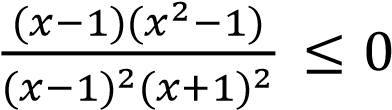 ;
;
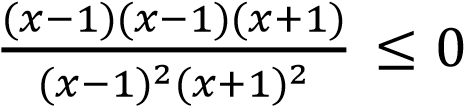 ;
;
 .
.
Далее применим метод интервалов. Для этого найдем нули левой части неравенства. Нули числителя и знаменателя совпадают, поэтому точки на числовой прямой будут выколоты.
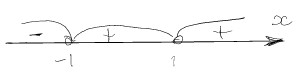
Ответ: 𝑥 ∈ (−∞; −1).
7. Примеры решение систем неравенств.
Важно! Чтобы решить систему неравенств, нужно: решить отдельно каждое неравенство; сравнить полученные решения каждого неравенства и получить общий ответ системы.
 7.1. Решить систему:
7.1. Решить систему: 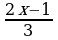 ≥ х – 2
≥ х – 2
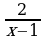 ≥ 4
≥ 4
Решение: решаем оба неравенства системы по отдельности.
1) Умножим первое неравенство системы на 3 и решим линейное неравенство. Получим: 2х – 1 ≥ 3х – 6
- х ≥ - 5
х ≤ 5
2) Перенесем все слагаемые второго неравенства системы в левую часть и приведем к общему знаменателю. Получим: 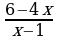 ≥ 0
≥ 0
Решим методом интервалов. Найдем нули числителя и знаменателя: х = 1,5 и х = 1. Знаменатель не равен 0, поэтому точка х=1 на числовой прямой будет выколота.
3) Определим знаки выражения на каждом промежутке.


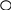




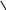

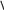
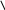
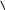





- +  - -
- -
1 1,5 5
Ответ: х € (1;1,5)

7.2. Решить систему неравенств:  х2 – 6х – 16 ≥ 0
х2 – 6х – 16 ≥ 0
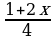 х - 1
х - 1
Решение: решаем оба неравенства системы по отдельности.
1) решаем первое неравенство, используя метод параболы.
у=х2 – 6х – 10 – квадратичная функция, график – парабола, а = 10, ветви вверх.
Найдем нули функции: х2 – 6х – 16 =0
D = (-6)2 – 4×1×(- 16) = 36 + 64 = 100 0, уравнение имеет 2 корня
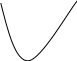
х1 = -2, х2 = 8







Изобразим схематично параболу: + +
-2 _ 8
2) Умножим второе неравенство на 4 и перенесем все слагаемые в одну часть:
1 + 2х
2х – 4х
2х 5
х 2,5

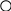






Изобразим на координатной прямой:
2,5
3) Пересекая множество решений первого и второго неравенства, получаем, что х € [8, +∞).
Ответ: [8, +∞).
Приложение 1


Приложение 2
(6 класс) Умножение и деление чисел с разными знаками: чтобы умножить(разделить) два числа с разными знаками, надо умножить(разделить) их модули и перед полученным числом поставить знак минус.
Умножение и деление двух отрицательных чисел: чтобы умножить(разделить) два отрицательных числа, надо умножить(разделить) их модули и перед полученным числом поставить знак плюс.
( 8 класс) Линейными неравенствами называются неравенства вида:
ax + b
ax + b 0
ax + b ≤ 0
ax + b ≥ 0
где a и b — любые числа, причем a≠0, x – неизвестная переменная.
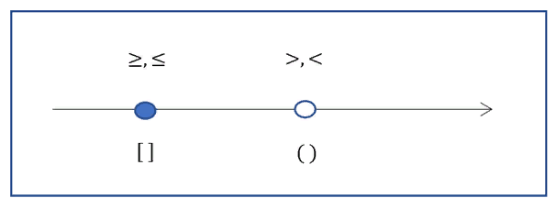
Обозначения на координатной прямой и в записи ответа в виде множества:
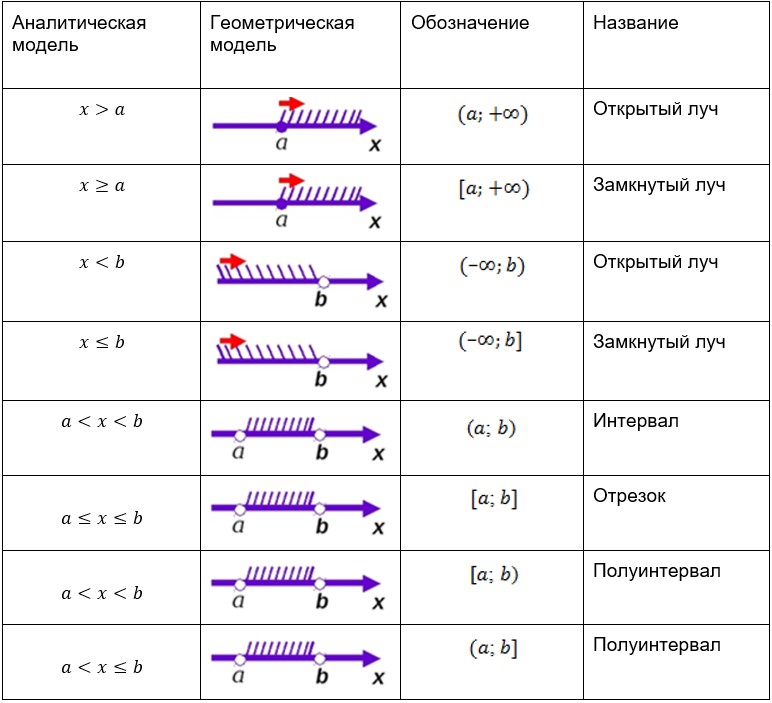
Сводная таблица числовых промежутков:
( 8 класс) Правила преобразования неравенств:
Правило 1. Любой член неравенства можно переносить из одной части неравенства в другую, меняя при этом знак на противоположный (т.е. при переносе через знак неравенства знаки при слагаемых меняются на противоположные, как в уравнении).
Правило 2. Обе части неравенства можно умножить/разделить на одно и то же положительное число, при этом получится неравенство, равносильное данному.
Правило 3. Обе части неравенства можно умножить/разделить на одно и то же отрицательное число, меняя знак неравенства на противоположный (т.е. знак на знак и наоборот; знак ≥ на знак ≤ и наоборот).
( 9 класс) Квадратное неравенство — это неравенство вида:
ax2 +bx + c 0
ax2 +bx + c
ax2 +bx + c ≥ 0
ax2 +bx + c ≤ 0
где a, b, c – числа, x≠0, x – переменная.
Для решения квадратного неравенства используется специальный способ, который называется методом интервалов.
Чтобы решить квадратное неравенство методом интервалов, нужно:
1.Перенести все члены неравенства в левую часть так, чтобы в правой остался только нуль.
2.Сделать так, чтобы при неизвестном «x2» стоял положительный коэффициент.
3.Приравнять левую часть неравенства к нулю и решить полученное квадратное уравнение.
4.Записать разложенное на множители выражение по формуле a(x-x1)(x-x2) . Полученные корни уравнения разместить на числовой оси в порядке возрастания.
5.Нарисовать «арки» для интервалов. Справа налево, начиная с «+», проставить, чередуя знаки «+» и «−».
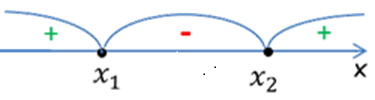
6.Выбрать необходимые интервалы и записать их в ответ.
(9 класс) Алгоритм решения квадратного неравенства с помощью параболы:
1.Приводим неравенство к виду aх2 +bх + с ≥ / ≤ 0
2. Рассматриваем функцию у= aх2 +bх + с, определяем направление ветвей и находим нули функции. Для этого решаем уравнение ах2 + bх + с = 0, находим его корни.
3. На оси Ох отмечаем точками корни уравнения. Если исходное неравенство нестрогое, точки – закрашенные. Если строгое - точки внутри пустые.
4. Схематично рисуем параболу, определяем знаки +/- на рисунке.
5.Выбираем нужные промежутки и записываем ответ.
Система неравенств состоит из нескольких неравенств с одной переменной. Эти неравенства объединяются фигурной скобкой (так же, как и уравнения в системах уравнений).
Задача состоит в том, чтобы найти все общие решения заданных неравенств.
Значение переменной, при котором каждое из неравенств системы становится верным числовым неравенством, называют решением системы неравенств.
Множество всех решений системы неравенств является общим решением (чаще всего — просто решением системы неравенств.)
Пример
Укажите множество системы неравенств:


Решение
Решение системы линейных неравенств сводится к решению линейного неравенства с дальнейшим анализом промежутков. В начале действуем аналогично первому случаю: переносим числа в правую часть, оставляя x слева:

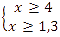
Сравним промежутки и выберем общий. Первое неравенство требует, чтобы x был больше 4, а второе — более 1,3. На координатной прямой это будет выглядеть следующим образом:
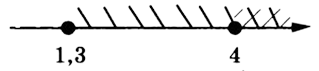

Промежутки перекрывают друг друга, начиная с 4. Значит, ответ выглядит следующим образом: [4;+∞ ).
Приложение 3
1) (√3 – 1,5)( 3 – 2х) 0
2) (3,5 - √13)( 3х – 7)
3) (√19 – 4,5)(5 – 3х) 0
4) (х – 3)(2х + 3)
5) (2х +1)(х – 1) 9
6) (3х – 2)(х+4) -11
7) (4х – 6)2 ≥ (6х – 4)2
8) (4х – 7)2 ≥ (7х – 4)2
9) (5х – 8)2 ≥ (8х – 5)2
10) (3х – 5)2 ≥ (5х – 3)2
11) (3х – 8)2 ≥ (8х – 3)2
12) (х – 1)2
13) (х – 7)2
14) (х – 3)2
15) (х – 4)2
16) (х – 9)2
17) (х – 5)2
18) х2 (- х2 – 25) ≤ 25(- х2 – 25)
19) 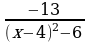 ≥ 0
≥ 0
20) 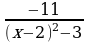 ≥ 0
≥ 0
21) 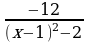 ≥ 0
≥ 0
22) 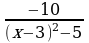 ≥ 0
≥ 0
23) 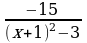 ≥ 0
≥ 0
24) 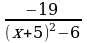 ≥ 0
≥ 0
25) 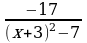 ≥ 0
≥ 0
26) 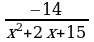 ≤ 0
≤ 0
27) 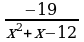 ≥ 0
≥ 0
28) 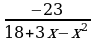 ≤ 0
≤ 0
29) 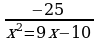 ≥ 0
≥ 0
30) 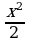
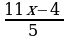
31) 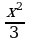 ≥
≥ 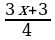
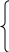
1) 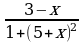 ≥ 0
≥ 0
 8 – 7х ≤ 12 – 3х
8 – 7х ≤ 12 – 3х
2) 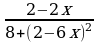 ≥ 0
≥ 0
 5 – 9х ≤ 37 – 5х
5 – 9х ≤ 37 – 5х
3) 4(9х + 3) – 9(4х +3) 3х
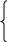 (х – 2)(х + 9)
(х – 2)(х + 9)
4) 7(3х + 2) – 3(7х + 2) 2х
(х – 5)(х + 8)






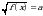 ,
, 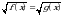 .
.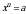 .Уравнения в целых числах.
.Уравнения в целых числах.




 5.
5. 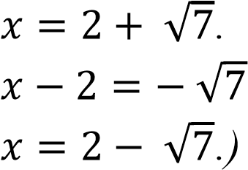 ;
; 
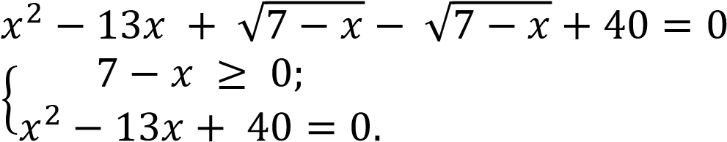 ;
; 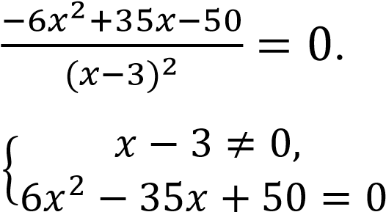
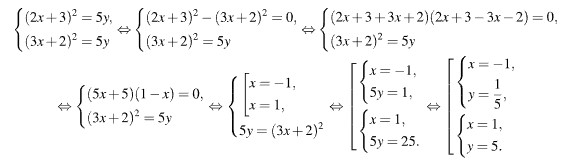
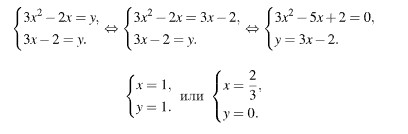

 ≥ 0
≥ 0




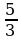
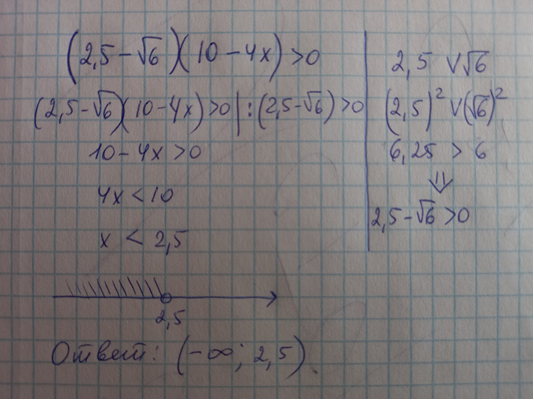

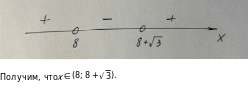


 7.1. Решить систему:
7.1. Решить систему: 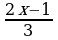 ≥ х – 2
≥ х – 2 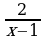 ≥ 4
≥ 4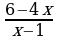 ≥ 0
≥ 0












 х2 – 6х – 16 ≥ 0
х2 – 6х – 16 ≥ 0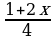 х - 1
х - 1























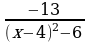 ≥ 0
≥ 0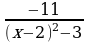 ≥ 0
≥ 0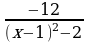 ≥ 0
≥ 0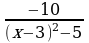 ≥ 0
≥ 0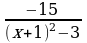 ≥ 0
≥ 0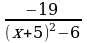 ≥ 0
≥ 0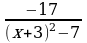 ≥ 0
≥ 0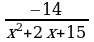 ≤ 0
≤ 0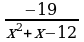 ≥ 0
≥ 0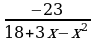 ≤ 0
≤ 0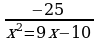 ≥ 0
≥ 0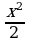
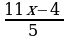
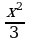 ≥
≥ 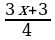
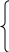
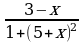 ≥ 0
≥ 0 8 – 7х ≤ 12 – 3х
8 – 7х ≤ 12 – 3х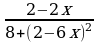 ≥ 0
≥ 0 5 – 9х ≤ 37 – 5х
5 – 9х ≤ 37 – 5х (х – 2)(х + 9)
(х – 2)(х + 9) 


















