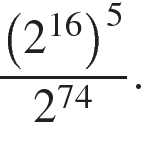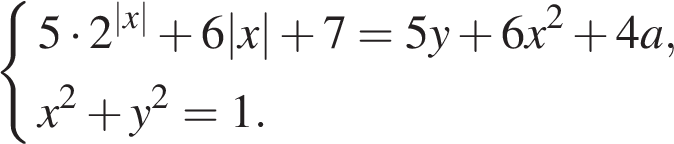Подготовка к промежуточной аттестации 10 класс

1. Задание 1 № 318581

Бегун пробежал 50 м за 5 секунд. Найдите среднюю скорость бегуна на дистанции. Ответ дайте в километрах в час.

2. Задание 2 № 525057

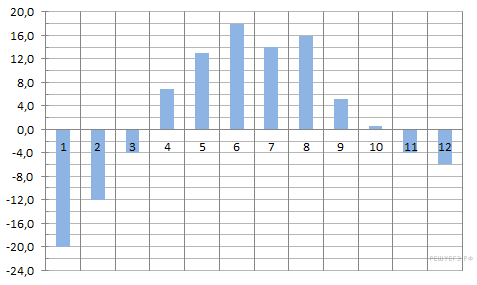
На диаграмме показана среднемесячная температура воздуха в Екатеринбурге (Свердловске) за каждый месяц 1973 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме, сколько было месяцев с положительной среднемесячной температурой в 1973 году.

3. Задание 3 № 501932

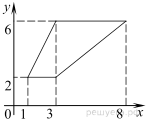
Найдите площадь трапеции, изображённой на рисунке.

4. Задание 4 № 1001

На экзамен вынесено 60 вопросов, Андрей не выучил 3 из них. Найдите вероятность того, что ему попадется выученный вопрос.

5. Задание 5 № 522114

Решите уравнение 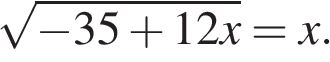  Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

6. Задание 6 № 56355

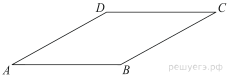Площадь ромба равна 66. Одна из его диагоналей равна 4. Найдите другую диагональ.

7. Задание 7 № 525090

На рисунке изображён график функции 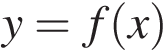  . На оси абсцисс отмечены точки −2, −1, 2, 4. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.

8. Задание 8 № 25681

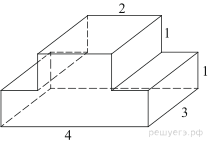Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

9. Задание 9 № 520902

Найдите значение выражения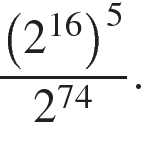 

10. Задание 10 № 518908

Для определения эффективной температуры звёзд используют закон Стефана—Больцмана, согласно которому 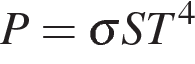  , где P — мощность излучения звезды (в ваттах),  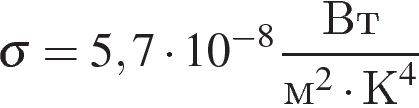 — постоянная, S — площадь поверхности звезды (в квадратных метрах), а T— температура (в кельвинах). Известно, что площадь поверхности некоторой звезды равна  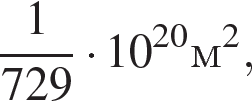 а мощность её излучения равна 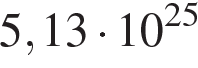 Вт. Найдите температуру этой звезды в кельвинах.

11. Задание 11 № 39749

На изготовление 486 деталей первый рабочий затрачивает на 9 часов меньше, чем второй рабочий на изготовление 621 детали. Известно, что первый рабочий за час делает на 4 детали больше, чем второй. Сколько деталей в час делает первый рабочий?

12. Задание 12 № 520494

Найдите точку максимума функции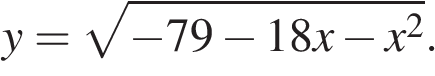 

13. Задание 13 № 521849

Решите уравнение: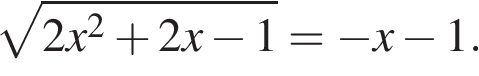 

14. Задание 14 № 517484

В треугольной пирамиде SABC известны боковые рёбра:   Основанием высоты этой пирамиды является середина медианы CM треугольника ABC. Эта высота равна 4.

а) Докажите, что треугольник ABC равнобедренный.

б) Найдите объём пирамиды SABC.

15. Задание 15 № 511239

Решите неравенство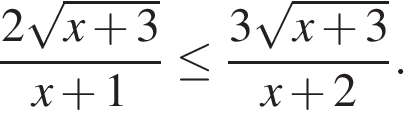 

16. Задание 16 № 516334

Дан треугольник ABC. Серединный перпендикуляр к стороне AB пересекается с биссектрисой угла BAC в точке K, лежащей на стороне BC.

а) Докажите, что 

б) Найдите радиус окружности, вписанной в треугольник AKC, если 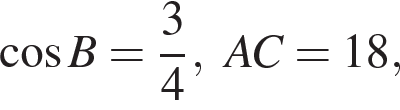  а площадь треугольника AKC равна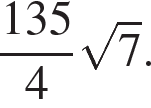 

17. Задание 17 № 509972

15-го января планируется взять кредит в банке на 39 месяцев. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастёт на r% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 20% больше суммы, взятой в кредит. Найдите r.

18. Задание 18 № 507481

Найти все значения a, при каждом из которых система

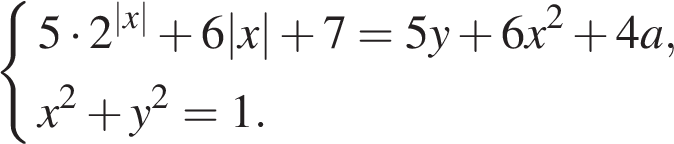
имеет единственное решение.

19. Задание 19 № 521010

На доске написано 10 различных натуральных чисел. Среднее арифметическое шести наименьших из них равно 5, а среднее арифметическое шести наибольших равно 15.

а) Может ли наименьшее из этих чисел равняться 3?

б) Может ли среднее арифметическое всех чисел равняться 11?

в) Найдите наибольшее значение среднего арифметического всех чисел.