Подготовка к заданию 23 ОГЭ по математике

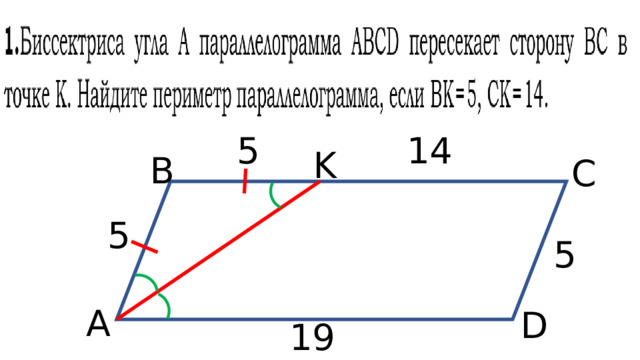
14

5

K

B

С

5

5

A

D

19

• BC = BK + KC = 5 + 14 = 19
• AD = 19, т. к. ABCD – параллелограмм
• ∆ ABK – равнобедренный.

∟ BAK = ∟KAD (AK - биссектриса),

∟ BKA = ∟KAD (накрест лежащие при ВС||AD и секущей АК). Значит, ∟BAK = ∟BKA.

4) АВ = ВК = 5

5) СD = 5, т. к. ABCD – параллелограмм

6) Р = 5+5+19+19= 48

Ответ: 48

Самостоятельно:

1. Биссектриса угла А параллелограмма ABCD пересекает сторону ВС в точке К. Найдите периметр параллелограмма, если ВК = 3, СК = 19.

2. Биссектриса угла А параллелограмма ABCD пересекает сторону ВС в точке К. Найдите периметр параллелограмма, если ВК = 5, СК = 11.

3. Биссектриса угла А параллелограмма ABCD пересекает сторону ВС в точке К. Найдите периметр параллелограмма, если ВК = 7, СК = 18.

4. Биссектриса угла А параллелограмма ABCD пересекает сторону ВС в точке К. Найдите периметр параллелограмма, если ВК = 6, СК = 13.

1. Высота АН ромба ABCD делит сторону CD на отрезки DH = 15 и СН = 2. Найдите высоту ромба.

A

17

17

D

B

15

17

Н

2

C

• DC = DH + HC = 15 + 2 = 17
• AD = 17, т. к. ABCD – ромб
• ∆ AHD – прямоугольный (АН - высота)
• По т. Пифагора:

Ответ: 8.

Самостоятельно:

1. Высота АН ромба ABCD делит сторону CD на отрезки DH = 24 и СН = 1. Найдите высоту ромба.

2. Высота АН ромба ABCD делит сторону CD на отрезки DH = 8 и СН = 2. Найдите высоту ромба.

3. Высота АН ромба ABCD делит сторону CD на отрезки DH = 12 и СН = 3. Найдите высоту ромба.

4. Высота АН ромба ABCD делит сторону CD на отрезки DH = 21 и СН = 8. Найдите высоту ромба.

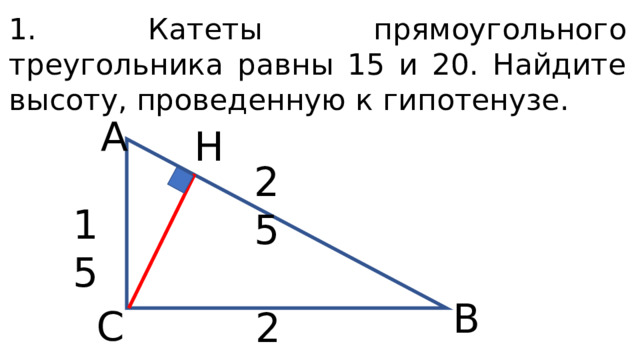
1. Катеты прямоугольного треугольника равны 15 и 20. Найдите высоту, проведенную к гипотенузе.

А

Н

25

15

В

С

20

Решение:

1. Найдем гипотенузу по т. Пифагора

2. Найдем площадь треугольника:

3. Из формулы площади треугольника найдем высоту:

Ответ: 12

Самостоятельно:

1. Катеты прямоугольного треугольника равны 18 и 24. Найдите высоту, проведенную к гипотенузе.

2. Катеты прямоугольного треугольника равны 15 и 36. Найдите высоту, проведенную к гипотенузе.

3. Катеты прямоугольного треугольника равны 21 и 28. Найдите высоту, проведенную к гипотенузе.

4. Катеты прямоугольного треугольника равны 10 и 24. Найдите высоту, проведенную к гипотенузе.

5. Катеты прямоугольного треугольника равны 21 и 75. Найдите высоту, проведенную к гипотенузе.

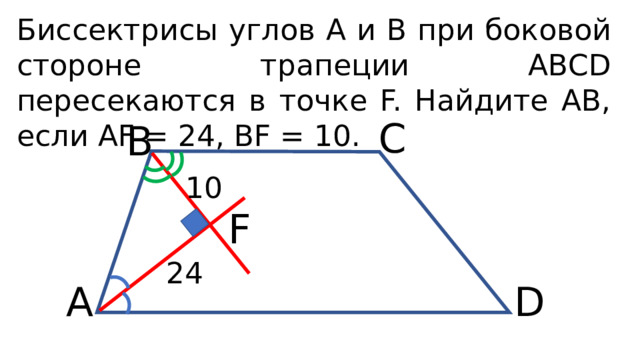
Биссектрисы углов А и В при боковой стороне трапеции АВСD пересекаются в точке F. Найдите AB, если AF = 24, BF = 10.

C

B

10

F

24

D

A

Решение:

1. ∟A + ∟B = 180°, т. к. односторонние при ВС||AD и секущей АВ,

2. АF и BF - биссектрисы углов А и В, то ∟BAF + ∟ABF = = 90°.

3. ∆ABF – прямоугольный, ∟AFB = 90°.

4. По т. Пифагора

Ответ: 26

Самостоятельно:

1. Биссектрисы углов А и В при боковой стороне трапеции АВСD пересекаются в точке F. Найдите AB, если AF = 16, BF = 12.

2. Биссектрисы углов А и В при боковой стороне трапеции АВСD пересекаются в точке F. Найдите AB, если AF = 20, BF = 15.

3. Биссектрисы углов А и В при боковой стороне трапеции АВСD пересекаются в точке F. Найдите AB, если AF = 15, BF = 8.

4. Биссектрисы углов А и В при боковой стороне трапеции АВСD пересекаются в точке F. Найдите AB, если AF = 32, BF = 34.

5. Биссектрисы углов А и В при боковой стороне трапеции АВСD пересекаются в точке F. Найдите AB, если AF = 24, BF = 7.

Прямая, параллельная стороне АС треугольника АВС, пересекает стороны АВ и ВС в точках М и N соответственно. Найдите BN, если MN = 11, AC = 44, NC = 18

В

N

M

11

18

С

А

44

Решение:

• ∆ АВС ∆MBN, по первому признаку подобия треугольников

∟ В – общий, ∟А = ∟М, т. к. соответственные при MN||AC и секущей АВ.

2. , BC = BN + NC = BN + 18

3.

44BN = 11·(BN + 18)

44BN = 11BN + 198

44BN – 11BN = 198

33BN = 198 | : 33

BN = 6

Ответ: 6.

Самостоятельно:

1. Прямая, параллельная стороне АС треугольника АВС, пересекает стороны АВ и ВС в точках М и N соответственно. Найдите BN, если MN = 16, AC = 20, NC = 15.

2. Прямая, параллельная стороне АС треугольника АВС, пересекает стороны АВ и ВС в точках М и N соответственно. Найдите BN, если MN = 15, AC = 25, NC = 22.

3. Прямая, параллельная стороне АС треугольника АВС, пересекает стороны АВ и ВС в точках М и N соответственно. Найдите BN, если MN = 17, AC = 51, NC = 32.

4. Прямая, параллельная стороне АС треугольника АВС, пересекает стороны АВ и ВС в точках М и N соответственно. Найдите BN, если MN = 22, AC = 55, NC = 36.

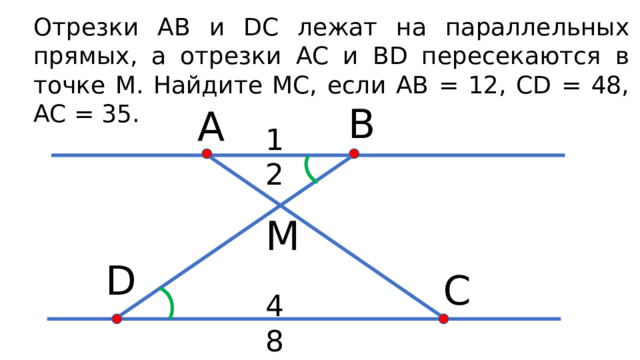
Отрезки АВ и DC лежат на параллельных прямых, а отрезки АС и BD пересекаются в точке М. Найдите МС, если АВ = 12, CD = 48, АС = 35.

В

А

12

M

D

С

48

Решение:

1. ∆АMB ∆DMC, по первому признаку подобия треугольников ∟AMВ = ∟DMC, т.к. вертикальные, ∟D = ∟B, т. к. накрест лежащие при АВ||DC и секущей DВ.

2. , AM = AC - MC = 35 - MC

3.

12MC = 48·(35 - MC)

12MC = 1680 – 48MC

12MC + 48MC = 1680

60MC = 1680 | : 60

MC = 28

Ответ: 28.

Самостоятельно:

1. Отрезки АВ и DC лежат на параллельных прямых, а отрезки АС и BD пересекаются в точке М. Найдите МС, если АВ = 12, CD = 48, АС = 35.

2. Отрезки АВ и DC лежат на параллельных прямых, а отрезки АС и BD пересекаются в точке М. Найдите МС, если АВ = 10, CD = 25, АС = 56.

3. Отрезки АВ и DC лежат на параллельных прямых, а отрезки АС и BD пересекаются в точке М. Найдите МС, если АВ = 13, CD = 65, АС = 42.

4. Отрезки АВ и DC лежат на параллельных прямых, а отрезки АС и BD пересекаются в точке М. Найдите МС, если АВ = 14, CD = 42, АС = 52.