Методические рекомендации
по проведению государственной итоговой аттестации по образовательным программам основного общего образования по математике в форме государственного выпускного экзамена
(письменная форма)
Организация экзамена для глухих и слабослышащих обучающихся имеет ряд особенностей. Для слабослышащих обучающихся аудитории для проведения экзамена оборудуются звукоусиливающей аппаратурой как коллективного, так и индивидуального пользования (см. п. 34 Порядка ГИА-9). При необходимости привлекается ассистент-сурдопереводчик. (см. п. 34 и 37 Порядка ГИА-9).
ППЭ может быть организован на базе любой образовательной организации.
Отсутствие специальной звукоусиливающей электроакустической аппаратуры (ЗУЭА) не может являться препятствием для проведения ГВЭ-9, так как обучающиеся активно пользуются индивидуальными слуховыми аппаратами. Нужны те условия для использования остаточного слуха, которые комфортны обучающимися в ОО АООП в связи с их специфическими техническими ресурсами и опытом их эксплуатации обучающимися. Это могут быть аппаратура для фронтального пользования, привычная обучающимся, или их собственные индивидуальные слуховые аппараты, рекомендованные сурдоцентром (для слабослышащих детей) или индивидуальной программой реабилитации – для глухих детей, являющихся инвалидами детства.
В продолжительность выполнения экзаменационной работы не включается время, выделенное на подготовительные мероприятия (инструктаж обучающихся, вскрытие пакетов с экзаменационными материалами, заполнение регистрационных полей экзаменационной работы, настройка технических средств).
Для обучающихся с ОВЗ, детей-инвалидов и инвалидов, а также тех, кто обучался по состоянию здоровья на дому, в образовательных организациях, в том числе санаторно-курортных, в которых проводятся необходимые лечебные, реабилитационные и оздоровительные мероприятия для нуждающихся в длительном лечении, продолжительность выполнения экзаменационной работы увеличивается на 1,5 часа.
Особенности экзаменационных материалов по математике ГВЭ-9 (письменная форма)
Письменный экзамен ГВЭ-9 по математике проводится
в нескольких форматах в целях учета возможностей разных категорий его участников: участников без ОВЗ и участников с ОВЗ.
При разработке экзаменационной модели соблюдалась преемственность с традиционными и новыми формами экзамена по математике для обучающихся, освоивших образовательные программы основного общего образования.
Участники ГВЭ-9 без ОВЗ и с ОВЗ (за исключением участников с задержкой психического развития) сдают экзамен по экзаменационным материалам, номер которых маркирован буквой «А».
Участники ГВЭ-9 с задержкой психического развития могут сдавать экзамен по экзаменационным материалам, номер которых маркирован буквой «К».
Экзаменационные материалы содержат маркировку «А»
Каждый вариант экзаменационной работы содержит 12 заданий,
из которых 10 заданий с заданий с кратким ответом, в которых необходимо записать ответ в виде целого числа или конечной десятичной дроби, и 2 задания с развернутым ответом.
Максимальный первичный балл за выполнение всей работы – 14.
Задание с развернутым ответом оценивается двумя экспертами. Существенным считается расхождение в 2 и более балла оценки за выполнение задания с развернутым ответом.
Рекомендуется следующая шкала перевода суммы первичных баллов
в пятибалльную систему оценивания.
Рекомендуемая шкала пересчета первичного балла в школьную отметку
| Отметка по пятибалльной шкале | «2» | «3» | «4» | «5» |
| Первичный балл | 0–3 | 4–6 | 7–9 | 10–14 |
На выполнение работы даётся 3 часа 55 минут (235 минут).
Необходимые справочные материалы выдаются вместе с текстом экзаменационной работы. При выполнении заданий ГВЭ-9 разрешается пользоваться линейкой.
Экзаменационные материалы содержат маркировку «К»
Каждый вариант экзаменационной работы, маркированного буквой «К», содержит 10 заданий с кратким ответом, в которых необходимо записать ответ в виде целого числа или конечной десятичной дроби.
Максимальный балл за всю работу – 10. Рекомендуется следующая шкала перевода суммы первичных баллов в пятибалльную систему оценивания.
Рекомендуемая шкала пересчета первичного балла в школьную отметку
| Отметка по пятибалльной шкале | «2» | «3» | «4» | «5» |
| Первичный балл | 0–2 | 3–5 | 6–8 | 9–10 |
На выполнение экзаменационной работы по математике даётся 3 часа 55 минут (235 минут).
Необходимые справочные материалы для выполнения экзаменационной работы выдаются вместе с текстом экзаменационной работы. При выполнении заданий разрешается пользоваться линейкой.
Вариант 1
Часть 1
Ответом к заданиям 1–10 является целое число или конечная десятичная дробь. Запишите ответ в поле ответа в тексте работы.
1
Найдите значение выражения: 5,3 - 9∙(-4,4)
2
Решите уравнение 2х2 + 3х-2 =0 Если уравнение имеет более одного корня, в ответ запишите больший из корней.
3
Найдите значение выражения 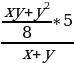 при х = 3, у = – 8
при х = 3, у = – 8
4
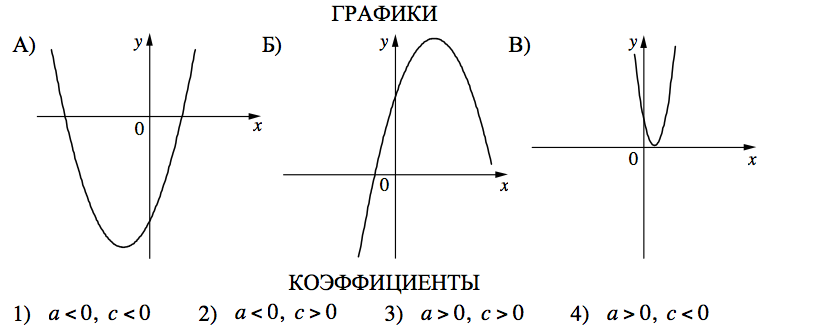
На рисунке изображены графики функций вида у = ах
2 + bx + c.
Установите соответствие между графиками функций и знаками коэффициентов а и с.
5
Укажите множество решений неравенства х -1 ≤ 3х+2

6
В треугольнике два угла равны 27º и 79º. Найдите его третий угол. Ответ дайте в градусах.
7
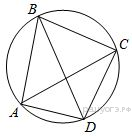
Четырёхугольник ABCD
вписан в окружность. Угол ABD равен 80º, угол CAD равен 34º. Найдите угол
ABC. Ответ дайте в градусах.
8
Какое из следующих утверждений верно? 1) Если два угла одного треугольника равны двум углам другого
треугольника, то такие треугольники подобны.
2) Диагонали ромба равны.
3) Тангенс любого острого угла меньше единицы.
В ответ запишите номер выбранного утверждения.
В ответе запишите номера выбранных утверждений без пробелов,
запятых и других дополнительных символов.
9
Принтер печатает одну страницу за 6 секунд. Сколько страниц можно напечатать на этом принтере за 9 минут?
10
Родительский комитет закупил 25 пазлов для подарков детям в связи с окончанием учебного года, из них 18 с машинами и 7 с видами городов.
Подарки распределяются случайным образом между 25 детьми, среди
которых есть Володя. Найдите вероятность того, что Володе достанется пазл с машиной.
Часть 2
Для записи решений заданий 11 и 12 и ответов к ним используйте дополнительный лист. Запишите сначала номер задания, затем чётко
и разборчиво решение и ответ.
11
Два автомобиля одновременно отправляются в 990-километровый пробег. Первый едет со скоростью на 9 км/ч большей, чем второй, и прибывает
к финишу на 1 час раньше второго. Найдите скорость первого автомобиля.
12
Биссектрисы углов B
и C
параллелограмма ABCD
пересекаются в точке M , лежащей на стороне AD. Докажите, что M — середина AD.
Вариант 2
Часть 1
Ответом к заданиям 1–10 является целое число или конечная десятичная дробь. Запишите ответ в поле ответа в тексте работы.
1
Найдите значение выражения 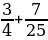
2
Решите уравнение 2х2 = 7х
Если уравнение имеет более одного корня, в ответ запишите меньший
из корней.
3
Найдите значение выражения 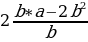 при a = – 79 , b = -2.
при a = – 79 , b = -2.
4
Установите соответствие между графиками функций и формулами, которые их задают. 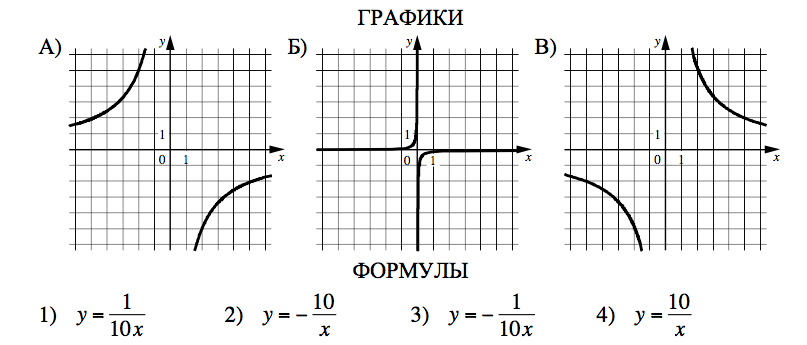
5
Укажите множество решений системы неравенств
х 8
8
9 –x0
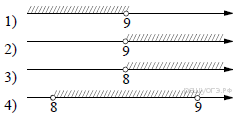
6
Катеты прямоугольного треугольника равны 18 и 24. Найдите гипотенузу этого треугольника.
7
Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOBравен 67º.
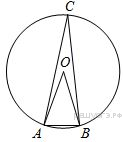
8
Какие из следующих утверждений верны?
1) Через точку, не лежащую на данной прямой, можно провести прямую,
параллельную этой прямой.
2) Если диагонали параллелограмма равны, то он является ромбом.
3) Для точки, лежащей на окружности, расстояние до центра окружности
равно радиусу.
В ответ запишите номера выбранных утверждений без пробелов, запятых
и других дополнительных символов.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
9
Спортивный магазин проводит акцию. Любая футболка стоит 200 рублей. При покупке двух футболок — скидка на вторую футболку 80%. Сколько
рублей придётся заплатить за покупку двух футболок в период действия
акции
10
Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,26. Покупатель в магазине выбирает одну шариковую ручку. Найдите
вероятность того, что эта ручка пишет хорошо.
Часть 2
Для записи решений заданий 11 и 12 и ответов к ним используйте дополнительный лист. Запишите сначала номер задания, затем чётко
и разборчиво решение и ответ.
11
Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути
со скоростью 70 км/ч, а вторую половину пути проехал со скоростью,
большей скорости первого на 21 км/ч, в результате чего прибыл вВ
одновременно с первым автомобилистом. Найдите скорость первого
автомобилиста.
12
Биссектрисы углов A
и B
трапеции ABCD
пересекаются в точке K
, лежащей на стороне CD. Докажите, что точка K равноудалена от прямыхAB, BC и AD
Вариант 3
Часть 1
Ответом к заданиям 1–10 является целое число или конечная десятичная дробь. Запишите ответ в поле ответа в тексте работы.
1
Найдите значение выражения 0,7∙ (-10)3 -20
2
Решите уравнение 7(х+2) =5х +18
3
Найдите значение выражения
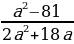 при a = - 0,5
при a = - 0,5
4
На рисунке изображены графики функций вида y = kx + b
. Установите соответствие между знаками коэффициентов k
и b
и графиками функций.
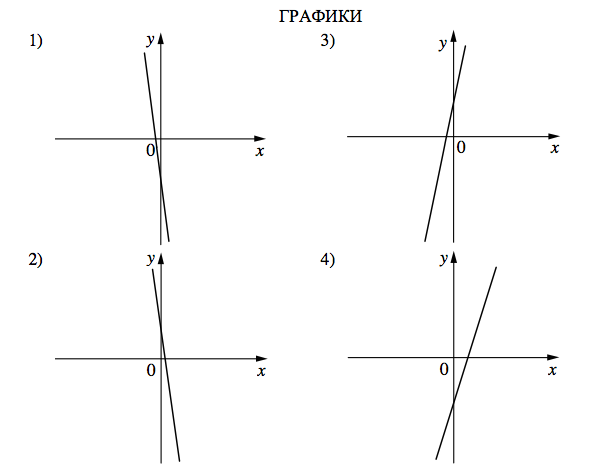
КОЭФФИЦИЕНТЫ
А) kb 0 Б) kbk 0, b
5
Укажите решение неравенства
х2– 250
1) 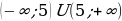 2)
2) 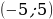 3)
3) 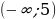 4)
4) 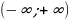
6
Сторона треугольника равна 16, а высота, проведённая к этой стороне,
равна 19. Найдите площадь треугольника.
7
В треугольнике ABC известно, что AC = 6, BC = 8 , угол Cравен 90º. Найдите радиус описанной около этоготреугольника окружности
.
8
Укажите номер верного утверждения
1) Площадь ромба равна произведению его диагоналей.
2) Любая медиана равнобедренного треугольника является его
биссектрисой.
3) Если в параллелограмме диагонали перпендикулярны, то это – ромб.
В ответе запишите номера выбранных утверждений без пробелов,
запятых и других дополнительных символов.
9
На тарелке лежат одинаковые на вид пирожки: 2 с мясом, 16 с капустой
и 2 с вишней. Рома наугад берёт один пирожок. Найдите вероятность того,
что пирожок окажется с вишней.
10
Площадь земель крестьянского хозяйства, отведённая под посадку
сельскохозяйственных культур, составляет 49 гектаров и распределена между
зерновыми культурами и картофелем в отношении 2:5. Сколько гектаров
занимает картофель?
Часть 2
Для записи решений заданий 11 и 12 и ответов к ним используйте дополнительный лист. Запишите сначала номер задания, затем чётко
и разборчиво решение и ответ.
11
Велосипедист выехал с постоянной скоростью из города А в город В,
расстояние между которыми равно 180 км. Отдохнув, он отправился обратно
в А, увеличив скорость на 5 км/ч. По пути он сделал остановку на 3 часа,
в результате чего затратил на обратный путь столько же времени, сколько
на путь из А в В. Найдите скорость велосипедиста на пути из А в В.
12
В выпуклом четырёхугольнике ABCD углы CDB и CAB равны. Докажите,
что углы BCA и BDA также равны.
Вариант 4
Часть 1
Ответом к заданиям 1–10 является целое число или конечная десятичная дробь. Запишите ответ в поле ответа в тексте работы.
1
Найдите значение выражения
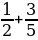
2
Найдите корень уравнения 2 + 3х = -7х-5
3
Найдите значение выражения
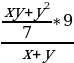 при х=1, у =7.
при х=1, у =7.
4
Установите соответствие между графиками функций и формулами, которые их задают.
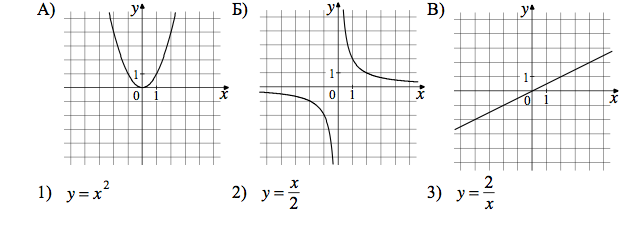
5
Решение какого из данных неравенств изображено на рисунке?
В ответе укажите номер правильного варианта.
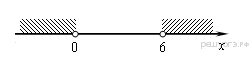
1) х2– 6х0
2)х2– 6х0
3)х2– 36х 0
4)х2– 36х 0
6
Отрезки AC и BD — диаметры окружности с центром O .
Угол ACB равен 16º. Найдите угол AOD. Ответ дайте в градусах.
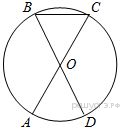
7
Найдите площадь ромба, если его диагонали равны 14 и 6.
8
Укажите номера верных утверждений.
1) Две прямые, перпендикулярные третьей прямой, перпендикулярны друг другу.
2) Диагонали ромба точкой пересечения делятся пополам.
3) Треугольник со сторонами 1, 3, 4 не существует.
В ответе запишите номера выбранных утверждений без пробелов,
запятых и других дополнительных символов.
9
Стоимость проезда в электричке составляет 171 рубль. Школьникам
предоставляется скидка 50%. Сколько рублей будет стоить проезд для
2 взрослых и 17 школьников?
10
На экзамене 40 билетов, Оскар
не выучил 12 из них. Найдите вероятность
того, что ему попадётся выученный билет.
Часть 2
Для записи решений заданий 11 и 12 и ответов к ним используйте дополнительный лист. Запишите сначала номер задания, затем чётко
и разборчиво решение и ответ.
11
Два велосипедиста одновременно отправляются в 140-километровый пробег.
Первый едет со скоростью на 14 км/ч большей, чем второй, и прибывает
к финишу на 5 часов раньше второго. Найдите скорость велосипедиста,
пришедшего к финишу вторым.
12
Основания BC и AD трапеции ABCD равны соответственно 3 и 12, BD =6.
Докажите, что треугольники CBD и BDA подобны.
Вариант 5
Часть 1
Ответом к заданиям 1–10 является целое число или конечная десятичная дробь. Запишите ответ в поле ответа в тексте работы.
1
Найдите значение выражения
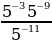
2
Найдите корень уравнения 3(х-2) = 2х + 8
3
Найдите значение выражения
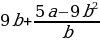
при a =9, b =36 .
4
На рисунке изображены графики функций вида y = kx + b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
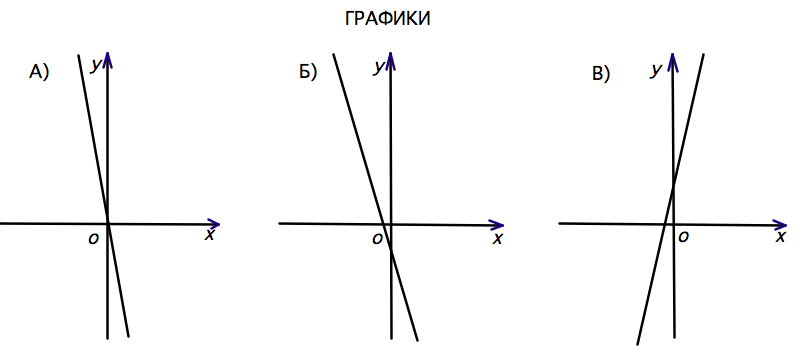
КОЭФФИЦИЕНТЫ
1) k 0 2) k 0, b 0 3) k
5
Укажите множество решений неравенства 81х
2

6
Сумма двух углов равнобедренной трапеции равна 178º. Найдите больший угол трапеции. Ответ дайте в градусах.

7
Периметр квадрата равен 84. Найдите площадь этого квадрата.

8
Укажите номера верных утверждений.
1) Через точку, не лежащую на данной прямой, можно провести прямую,
Параллельную этой прямой.
2) Через любую точку, лежащую вне окружности, можно провести две
касательные к этой окружности.
3) Если стороны одного четырехугольника соответственно равны
сторонам другого четырехугольника, то такие четырехугольники равны.
В ответе запишите номера выбранных утверждений без пробелов,
запятых и других дополнительных символов
9
Плата за телефон в этом году составляет 420 рублей в месяц. В следующем
году она увеличится на 5%. Сколько рублей придётся платить ежемесячно
за телефон в следующем году?
10
На экзамене 25 билетов, Сергей не выучил 3 из них. Найдите вероятность того, что ему попадётся выученный билет.
Часть 2
Для записи решений заданий 11 и 12 и ответов к ним используйте дополнительный лист. Запишите сначала номер задания, затем чётко
и разборчиво решение и ответ.
11
Моторная лодка прошла против течения реки 210 км и вернулась в пункт
отправления, затратив на обратный путь на 4 часа меньше, чем на путь
против течения. Найдите скорость лодки в неподвижной воде, если скорость
течения реки равна 3 км/ч.
12
Биссектрисы углов C и D параллелограмма ABCD пересекаются
в точке L, лежащей на стороне AB. Докажите, что L — середина AB.





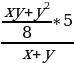 при х = 3, у = – 8
при х = 3, у = – 8 


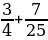
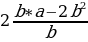 при a = – 79 , b = -2.
при a = – 79 , b = -2. 
 8
8

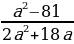 при a = - 0,5
при a = - 0,5 
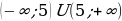 2)
2) 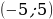 3)
3) 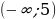 4)
4) 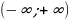
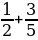
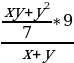 при х=1, у =7.
при х=1, у =7. 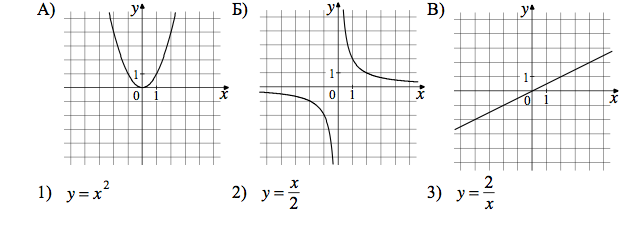


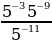
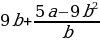 при a =9, b =36 .
при a =9, b =36 . 













