Тесты по теме: «Подобие треугольников» (9 класс)
1 вариант
-
Укажите условия, при которых 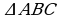 и
и 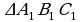 были бы подобны по третьему признаку.
были бы подобны по третьему признаку.
а)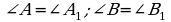 ; в)
; в)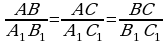 ;
;
б)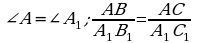 ; г)
; г)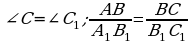 .
.
-
У треугольников АВС и DEF равны углы А и D. Какого условия не достает для того, чтобы утверждать, что эти треугольники подобны по первому признаку:
а)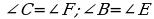 ; б)
; б)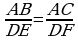 ; в)
; в) 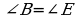 ; г)
; г)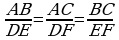 .
.
-
В треугольниках АВС и MNK 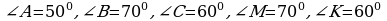 . Чему равен угол N?
. Чему равен угол N?
а)500; б)600; в)700.
-
Установите по рисунку, верно ли данное утверждение: 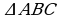 ~
~
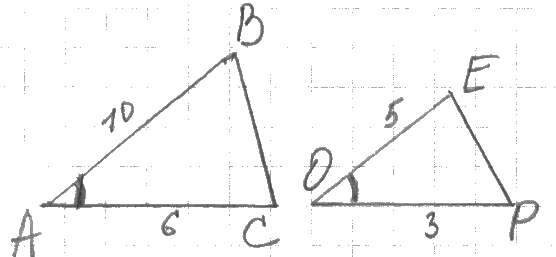
а)ДА; б)НЕТ; в)Не возможно установить.
-
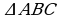 ~
~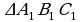 , АВ=4, ВС=6, АС=7, А1В1=8. Сторона В1С1 равна:
, АВ=4, ВС=6, АС=7, А1В1=8. Сторона В1С1 равна:
а)3; б)12; в)14.
-
В треугольниках ABC и 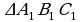
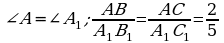 .
.
Если ВС=10, то В1С1 равна:
а)25; б) 4; в) 5.
-
Соответствующие катеты двух подобных прямоугольных треугольников равны 5 дм и 10 дм. Найдите гипотенузу большего треугольника, если гипотенуза меньшего равна 7 дм.
а)14; б) 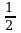 ; в) 2.
; в) 2.
Тест по теме: «Подобие треугольников» (8 класс)
2 вариант
-
Укажите условия, при которых 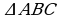 и
и 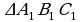 были бы подобны по первому признаку.
были бы подобны по первому признаку.
а)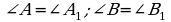 ; в)
; в)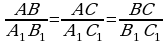 ;
;
б)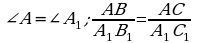 ; г)
; г)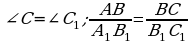 .
.
-
У треугольников АВС и DEF равны углы А и D. Какого условия не достает для того, чтобы утверждать, что эти треугольники подобны по второму признаку:
а)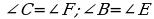 ; б)
; б)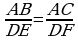 ; в)
; в) 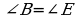 ; г)
; г)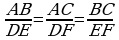 .
.
-
В треугольниках АВС и MNK 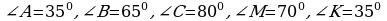 . Чему равен угол N?
. Чему равен угол N?
а)350; б)750; в)800.
-
Установите по рисунку, верно ли данное утверждение: 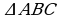 ~
~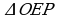
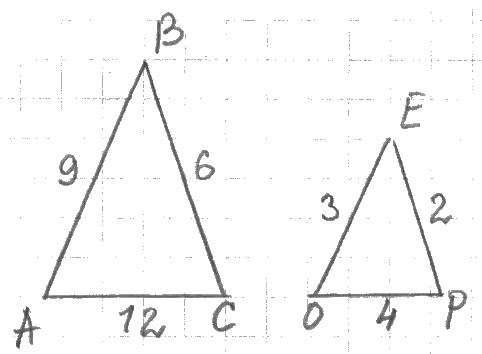
а)ДА; б)НЕТ; в)Не возможно установить.
-
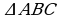 ~
~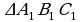 , АВ=2, ВС=3, АС=1, А1В1=8. Сторона В1С1 равна:
, АВ=2, ВС=3, АС=1, А1В1=8. Сторона В1С1 равна:
а)12; б)4; в)6.
-
В треугольниках ABC и 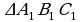
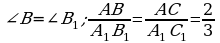 .
.
Если ВС=12, то В1С1 равна:
а)6; б) 18; в) 3.
-
Соответствующие катеты двух подобных прямоугольных треугольников равны 6 м и 18 м. Найдите гипотенузу меньшего треугольника, если гипотенуза большего равна 27 дм.
а) 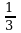 ; б) 3; в) 9.
; б) 3; в) 9.
Теоретический опрос «Подобие треугольников» (9 класс)
Подобные треугольники — треугольники, у которых соответственно равны, а одного пропорциональны сторонам другого треугольника.
Коэффициент — число k, равное отношению сторон подобных треугольников.
Сходственные стороны подобных треугольников — стороны, лежащие напротив углов.
-
Первый признак
Если два одного треугольника соответственно равны . другого треугольника, то треугольники .
-
Третий признак
Если одного треугольника трём сходственным сторонам другого, то подобны.
-
Свойства подобных треугольников:
Теоретический опрос «Подобие треугольников» (8 класс)
Подобные треугольники — треугольники, у которых соответственно равны, а одного пропорциональны сторонам другого треугольника.
Коэффициент — число k, равное отношению сторон подобных треугольников.
Сходственные стороны подобных треугольников — стороны, лежащие напротив углов.
-
Первый признак
Если два одного треугольника соответственно равны . другого треугольника, то треугольники .
-
Третий признак
Если одного треугольника трём сходственным сторонам другого, то подобны.
-
Свойства подобных треугольников:
| Тест. Подобные треугольники Заполните пропуски (многоточия), чтобы получилось верное высказывание. ВАРИАНТ 1 1. Запись 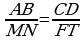 означает, что отрезки АВ означает, что отрезки АВ и CD ... отрезкам MN и FT. 2. На рисунке изображен параллелограмм ABCD, поэтому подобными являются треугольники ... и .... 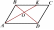
3. На рисунке АС || МК, поэтому треугольник МВК подобен треугольнику .... 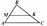
4. Если угол В равен ..., то изображенные на рисунке треугольники ABC и KNM подобны. 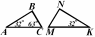
5. На рисунке МК || АС, АВ = 15 см, МВ = 5 см, АС = 30 см. Длина отрезка МК = ... . 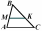
6. На рисунке изображена трапеция ABCD, причем АО = 27 см, ВО = 18 см, ОС = 21 см. Длина отрезка OD равна .... 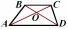
-
Площади двух подобных многоугольников равны 75 см2 и 300 см2. Одна из сторон второго многоугольника равна 9 см. Поэтому сходственная сторона первого многоугольника равна .... -
Сходственные стороны двух подобных треугольников равны 5 дм и 10 дм. Периметр первого треугольника равен 60 дм, периметр второго треугольника равен .... 9*. Известно, что ∆АВС - прямоугольный треугольник с прямым углом С, a CD - высота, проведенная из вершины С к гипотенузе АВ. Из подобия треугольников ... и ... следует, что AC2 =AB*AD.
| Тест. Подобные треугольники Заполните пропуски (многоточия), чтобы получилось верное высказывание. ВАРИАНТ 2 1. Запись 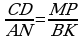 означает, что отрезки CD означает, что отрезки CD и MP ... отрезкам AN и BK. 2. На рисунке изображен параллелограмм АВСD, поэтому подобными являются треугольники ... и .... 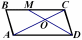
3. На рисунке АВ || KD, поэтому треугольник DKC подобен треугольнику .... 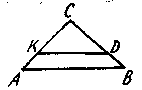
4. Если АС = ..., KN = ..., то изображенные на рисунке треугольники ABC и KNM подобны. 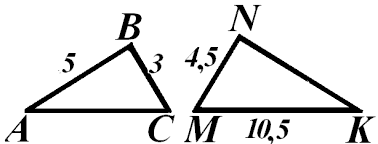
5. На рисунке МК || АС, ВК = 20 см, МК = 10 см, ВС = 30 см. Длина отрезка АС = ... . 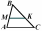
6. На рисунке изображена трапеция ABCD, причем АО = 20 см, ОС = 3 см, AD = 30 см. Длина отрезка ВС = ... . 
-
Сходственные стороны двух подобных многоугольников равны 20 см и 10 см. Площадь большего многоугольника равна 160 см2, площадь меньшего многоугольника равна .... -
Периметры подобных треугольников равны 75 см и 300 см. Одна из сторон большего треугольника равна 20 см, сходственная сторона меньшего треугольника равна .... 9*. Известно, что ∆АВС - прямоугольный треугольник с прямым углом С, a CD - высота, проведенная из вершины С к гипотенузе АВ. Из подобия треугольников ... и ... следует, что ВС2 = AB*BD.
|
| Тест. Подобные треугольники Установите, истинны или ложны следующие высказывания: Вариант 1 -
Два одноименных многоугольника называются подобными, если углы одного соответственно равны углам другого и сходственные стороны пропорциональны. -
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны. -
Два равносторонних треугольника всегда подобны. -
Если три стороны одного треугольника соответственно пропорциональны трем сторонам другого треугольника, то такие треугольники подобны. -
Периметры подобных многоугольников относятся как сходственные стороны. -
Стороны одного треугольника имеют длины 3 см, 4 см и 6 см. Стороны другого треугольника равны 9 см, 14 см и 18 см. Подобны ли эти треугольники? -
Два равнобедренных треугольника подобны, если их углы при вершине равны, и боковые стороны пропорциональны. -
Два прямоугольных треугольника подобны, если имеют по равному острому углу. -
Если два угла одного треугольника равны 60° и 50°, а два угла другого треугольника равны 50° и 80°, то такие треугольники подобны. -
Если каждую сторону треугольника уменьшить в 2,5 раза, то получится треугольник, подобный первоначальному. -
Два ромба всегда подобны. -
Два равнобедренных треугольника подобны, если их основания пропорциональны.
| Тест. Подобные треугольники Установите, истинны или ложны следующие высказывания: Вариант 2. -
Два треугольника называются подобными, если их углы соответственно равны и стороны пропорциональны. -
Если два треугольника имеют по равному углу, а стороны, заключающие эти углы, пропорциональны, то такие треугольники подобны. -
Два квадрата всегда подобны. -
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники подобны. -
Стороны одного треугольника имеют длины 4 м, 5 м и 6 м. Стороны другого треугольника равны 12 м, 8 м и 10 м. Тогда эти треугольники подобны. -
Площади подобных треугольников относятся как квадраты сходственных сторон. -
Два параллелограмма всегда подобны. -
Если два угла одного треугольника равны 45° и 75°, а два угла другого треугольника равны 60° и 45°, то такие треугольники подобны. -
Два прямоугольных треугольника подобны, если катеты одного треугольника соответственно пропорциональны катетам другого. -
Если каждую сторону треугольника уменьшить в 3 раза, то получится треугольник, подобный первоначальному. -
Два равнобедренных треугольника подобны, если угол при основании одного треугольника равен углу при основании другого. -
Два равнобедренных треугольника подобны, если их боковые стороны пропорциональны.
|
Признаки подобия треугольников
Вариант №1
1. У треугольников АВС и KLM равны углы А и К. Какого условия недостаёт, чтобы утверждать, Что эти треугольники подобны по первому признаку?
1) 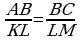 ; 2) АВ = KL, АС = КМ; 3)
; 2) АВ = KL, АС = КМ; 3) 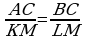 ; 4) угол В равен углу L.
; 4) угол В равен углу L.
2. Стороны одного треугольника равны 3 см, 6 см и 7 см, а стороны подобного ему треугольника равны 15 см и 35 см. Найдите длину третьей стороны:
1) 70 см; 2) 7,5 см; 3) 30 см; 4) ответ не указан.
3. Стороны угла К пересечены прямыми АВ и СД, причём точки А и С лежат на одной стороне угла (А лежит между К и С), а В и Д – на другой стороне (В лежит между К и Д). Какой должна быть длина отрезка АС, чтобы прямые АВ и СД были параллельны, если КА = 3,6 см, КВ = 4,8 см, ВД = 2,4 см?
1) 5,4 см; 2) 1,8 см; 3) 3,2 см; 4) 2 см.
4. ВС и АД – основания трапеции АВСД. Угол АВД равен углу ВСД. ВС = 4 см, ДС = 6 см, ВД = 8 см. Найдите АД:
1) 16 см; 2) 3 см; 3) 12 см; 4) 10 см.
5. На сторонах АВ и ВС треугольника АВС отмечены соответственно точки К и L, так , что KL параллельно АС. Площадь треугольника КBL равна 84 см², а площадь треугольника АВС равна 336 см², АС = 30 см. Найдите КL:
1) 7,5 см; 2) 10 см; 3) 15 см; 4) ответ не указан.
Признаки подобия треугольников
Вариант №2
1.Какие условия должны быть выполнены для того, чтобы треугольники АВС и КLМ были подобны по второму признаку?
1)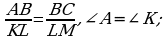 2) АВ = KL, АC = KM,
2) АВ = KL, АC = KM,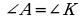 ; 3)
; 3) 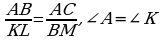 ; 4)
; 4) 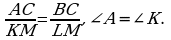
2. Стороны одного треугольника равны 3 см, 7 см и 6 см, а две стороны подобного ему треугольника равны 10,5 см и 4,5 см. Найдите длину третьей стороны:
1) 4 см; 2) 9 см; 3) 4,5 см; 4) ответ не указан.
3. Дан треугольник АВС и внутри него отрезок КМ, параллельный АС, причём 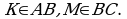 Найдите МС, если АВ = 18 см, ВК = 6 см, ВМ = 4 см:
Найдите МС, если АВ = 18 см, ВК = 6 см, ВМ = 4 см:
1) 12 см; 2) 16 см; 3) 6 см; 4) 8 см.
4. В трапеции АВСД углы АВС и АСД равны. Найдите диагональ АС, если основания ВС и АД соответственно равны 24 см и 54 см:
1) 18 см; 2) 30 см; 3) 36 см; 4) 72 см.
5. Дан треугольник АВС,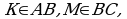 причём отрезок КМ параллельный АС. Площадь треугольника КВМ равна 9 см², ВМ = 6 см, МС = 2 см. Найдите площадь треугольника АВС:
причём отрезок КМ параллельный АС. Площадь треугольника КВМ равна 9 см², ВМ = 6 см, МС = 2 см. Найдите площадь треугольника АВС:
1) 12 см²; 2) 16 см²; 3) 81 см²; 4) ответ не указан
«Подобие треугольников» (8 класс)
Найти подобные треугольники на чертежах:
Задание 1:
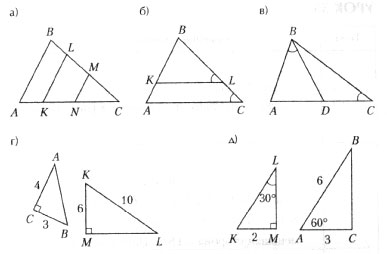
Задание 2:
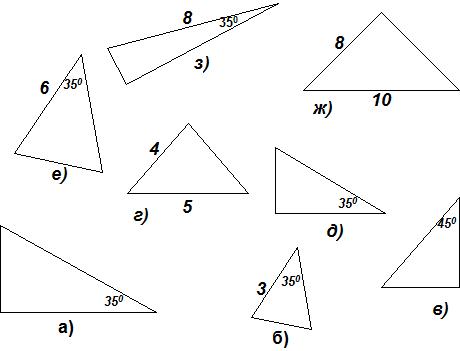
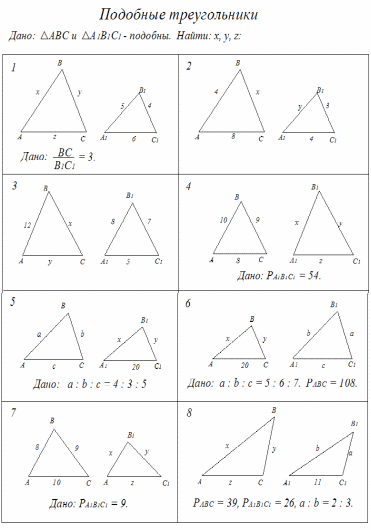







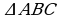 и
и 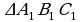 были бы подобны по третьему признаку.
были бы подобны по третьему признаку.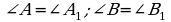 ; в)
; в)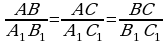 ;
;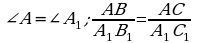 ; г)
; г)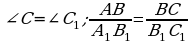 .
.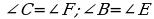 ; б)
; б)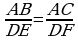 ; в)
; в) 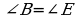 ; г)
; г)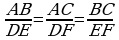 .
.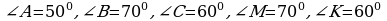 . Чему равен угол N?
. Чему равен угол N? 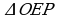
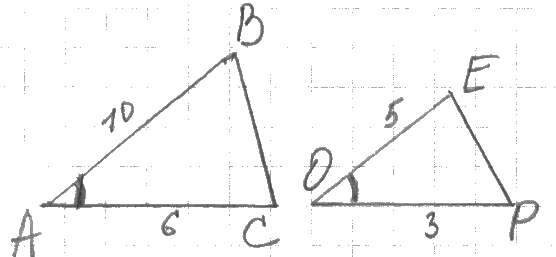
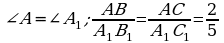 .
. 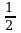 ; в) 2.
; в) 2.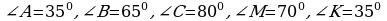 . Чему равен угол N?
. Чему равен угол N? 
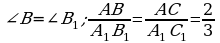 .
. 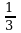 ; б) 3; в) 9.
; б) 3; в) 9.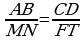 означает, что отрезки АВ
означает, что отрезки АВ
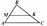
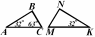
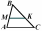

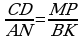 означает, что отрезки CD
означает, что отрезки CD

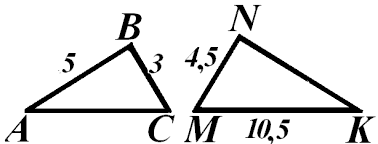
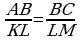 ; 2) АВ = KL, АС = КМ; 3)
; 2) АВ = KL, АС = КМ; 3) 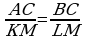 ; 4) угол В равен углу L.
; 4) угол В равен углу L.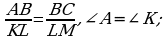 2) АВ = KL, АC = KM,
2) АВ = KL, АC = KM,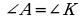 ; 3)
; 3) 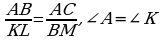 ; 4)
; 4) 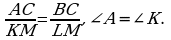
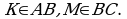 Найдите МС, если АВ = 18 см, ВК = 6 см, ВМ = 4 см:
Найдите МС, если АВ = 18 см, ВК = 6 см, ВМ = 4 см: 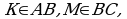 причём отрезок КМ параллельный АС. Площадь треугольника КВМ равна 9 см², ВМ = 6 см, МС = 2 см. Найдите площадь треугольника АВС:
причём отрезок КМ параллельный АС. Площадь треугольника КВМ равна 9 см², ВМ = 6 см, МС = 2 см. Найдите площадь треугольника АВС: 




















