Подобие в математике и реальной жизни. Решение задач.

Подобие в математике и реальной жизни

Презентацию подготовила: Шарифулина Е.Н., учитель математики

В геометрии фигуры одинаковой формы принято называть подобными.

Подобными являются любые два круга, два квадрата.

Тема урока : Подобие треугольников

• Определение подобных треугольников.
• Признаки подобия треугольников.
• Свойства площадей и периметров подобных треугольников.

Содержание:

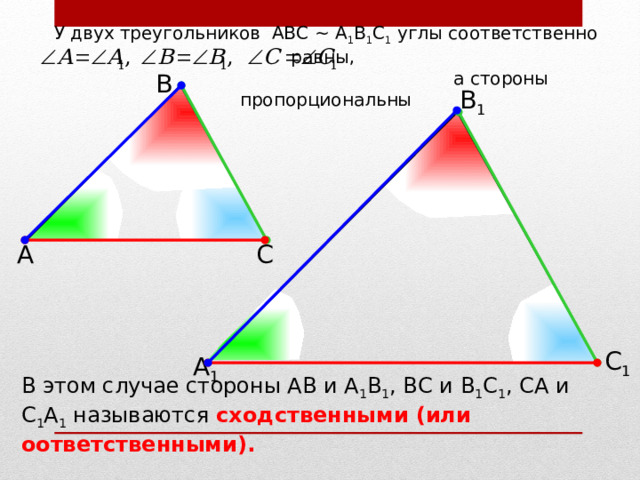
У двух треугольников АВС ~ А 1 В 1 С 1 углы соответственно равны,

а стороны пропорциональны

В

В 1

А

С

С 1

А 1

В этом случае стороны АВ и А 1 В 1 , ВС и В 1 С 1 , СА и С 1 А 1 называются сходственными (или оответственными).

M

N

K

Определение подобных треугольников:

B

C

A

Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника соответственно пропорциональны сходственным сторонам другого.

В

В 1

А

С

А 1

С 1

7

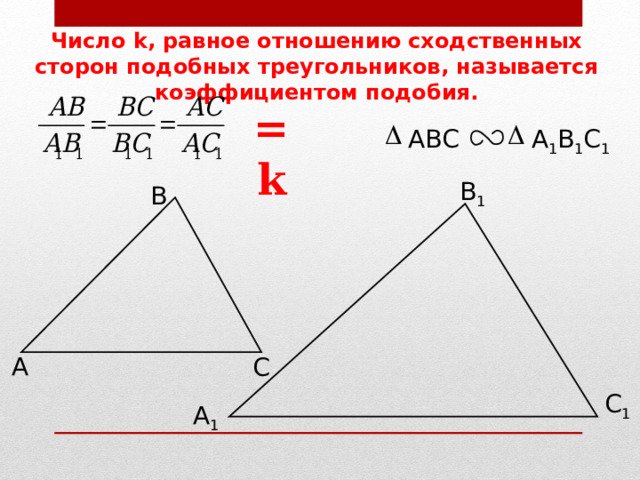
Число k, равное отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.

= k

ABC

A 1 B 1 C 1

В 1

В

А

С

С 1

А 1

9

20 см

15 см

B

K

Задача №1

P=26 см

M

N

C

A

30 см

Найти: NK, KM, NM.

Решение:

1) Если ∆ ABC ~∆ NKM, то

2)

• Площади подобных треугольников относятся, как коэффициент подобия в квадрате.

Свойства площадей и периметров подобных треугольников:

N

 ABC ∞  MNK

B

S  ABC

= k 2

S  MNK

A

C

K

M

9 см

Задача №3

K

В

S=75 м 2

S=300 м 2

M

N

А

С

Найти: NK.

Решение:

1) Если ∆ NKM ~∆ АВС, то

2)

Признаки подобия прямоугольных треугольников:

• Если два угла одного треугольника, соответственно равны двум углам другого треугольника , то такие треугольники подобны .

B

N

K

A

C

M

 ABC ∞  MNK

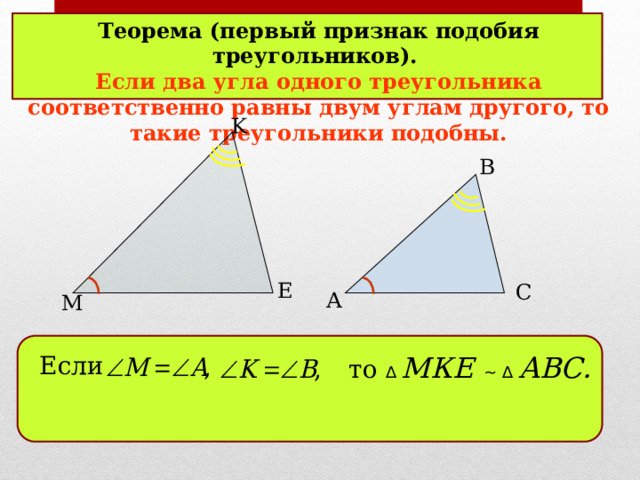
Теорема (первый признак подобия треугольников).

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

K

В

E

С

А

M

Если

то ∆ МКЕ ~ ∆ АВС.

B

№ 4

C

E

D

A

В задачах №4и№5 объяснить подобие треугольников .

E

E

C

B

D

A

№ 5

B

P

K

C

A

B

B

K

P

C

A

Задача №6

Задача № 7

ABC

А 1 В 1 С 1

Дано:

Найдите: х, у,z.

В

В 1

6см

7см

y

35см

х

30см

А

С

8см

С.М. Саврасова, Г.А. Ястребинецкий «Упражнения по планиметрии на готовых чертежах»

С 1

z

А 1

40см

Далее

20

Задача № 8

DE||AC

Найти: AB; BC.

B

8

x+6

E

D

10

x

A

C

15

a||b

Найти: x; y.

Задача №9

y

D

E

a

5

2x-3

x

4

B

A

y-1

C

b

Задача №10

Задача №11

Список использованных ресурсов: