

Разбор заданий ОГЭ
тип 1-5
по математике
Содержание
тип. Участки (4)
тип. Бани (8)
тип. Теплицы (13)
тип. Листы бумаги (18)
тип. Шины (23)
тип. ОСАГО (28)
тип. Путешествия (35)
тип. Квартиры (41)
тип. Зонты (47)
1 тип. Участки
Дан план участка.
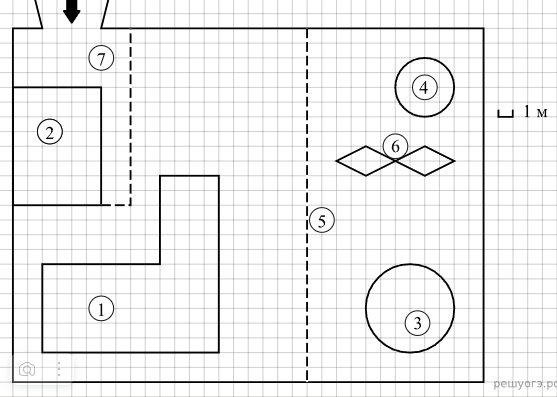
При входе на участок напротив ворот находится гараж, а за гаражом – жилой дом.
Площадь, занятая гаражом, равна 54 кв. м.
На газоне имеются круглый бассейн, беседка и ромбовидная клумба. Беседка отмечена на плане цифрой 4.
При въезде на участок имеется площадка, вымощенная тротуарной плиткой с размером каждой плитки 0,2 м. х 0,2 м и обозначенная на плане цифрой 7.
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк перенесите последовательность четырёх цифр.
| Объекты | Жилой дом | Гараж | Бассейн | Клумба |
| Цифры |
|
|
|
|
Решение. Читаем ещё раз условие задачи.
Напротив ворот находится гараж, на схеме – номер 2. За гаражом отмечен жилой дом ̶ это номер 1. Клумба имеет форму ромба, значит – номер 6. И наконец, бассейн, он обозначен цифрой 3, т.к. под номером 4 отмечена беседка. Осталось внести результаты в таблицу.
| Объекты | Жилой дом | Гараж | Бассейн | Клумба |
| Цифры | 1 | 2 | 3 | 6 |
Ответ: 1236.
Найдите площадь, которую занимает клумба. Ответ дайте в квадратных метрах.
Решение. Площадь ромба можно найти как половину произведения диагоналей. Получим,
Ответ: 12.
Тротуарная плитка продаётся в упаковках по 45 штук. Сколько упаковок плитки понадобилось, чтобы выложить площадку перед гаражом?
Решение. Найдём сначала общую площадь, которую необходимо выложить плиткой. Она состоит из двух прямоугольников 8×4 и 9×2. Итак, площадь 32 + 18
= 50 кв. м.
Теперь вычислим площадь одной плитки: 0,2×0,2 = 0,04 кв. м. Далее разделим площадь территории перед гаражом на площадь одной плитки:
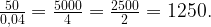
Таким образом, необходимо 1250 штук плиток. Но плитки продаются только упаковками. Осталось разделить на 45:
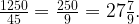
Т.к. невозможно купить нецелое число упаковок, то необходимо их купить или 27, или 28. А всё же сколько? Но 27 упаковок не хватит. Тогда придётся купить
28 (это даже к лучшему, оставшиеся плитки пригодятся для замены поврежденных).
Ответ: 28.
Во сколько раз площадь бассейна больше площади беседки?
Решение. Бассейн и беседка имеют круглую форму. Напомним, что площадь круга равна .
Выясним, какие радиусы имеют бассейн и беседка. По рисунку видно, что радиус бассейна равен 3, а радиус беседки равен 2. Составим и вычислим отношение площадей:
Ответ: 2,25.
Хозяин участка хочет обновить газон к новому дачному сезону. Для этого он планирует купить семена газонной травы. Цена одной упаковки семян, её масса и рекомендуемый расход указаны в таблице.
Во сколько рублей обойдётся наиболее дешёвый вариант? (Территорию, занятую бассейном и беседкой, засевать не предполагается. Клумбу планируется убрать, и на её место тоже засеять газонную траву. Число π возьмите равным 3. Считаем, что все купленные семена - одного сорта).
| Поставщик | Цена 1 уп. семян (руб.) | Масса 1 уп. семян (кг.) | Рекомендуемый расход 1 уп. семян (кв. м.) |
| А | 520 | 1,5 | 60 |
| Б | 350 | 1,2 | 40 |
Решение. Заметим, что масса упаковки семян в задаче ̶ это избыточная информация, никак не влияющая на расход, который зависит от засеваемой площади. Найдём сначала площадь, которую необходимо засеять, по рисунку ̶ это прямоугольник 24×12. Но на газоне расположены бассейн и беседка, и их площади нет необходимости учитывать при расчётах (там травы нет). При этом клумбу планируется тоже засеять травой, значит, её площадь не вычитается. Итак,
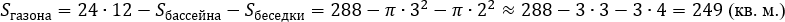
Далее произведём расчёты по каждому поставщику в отдельности.
| Поставщик | Необходимое количество упаковок семян | Стоимость закупки семян (руб.) |
| А | 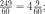 5 упаковок |
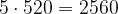
|
| Б | 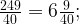 7 упаковок 7 упаковок |
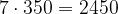
|
| В | 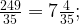 8 упаковок 8 упаковок |
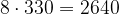
|
| Г | 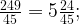 6 упаковок 6 упаковок |
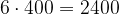
|
Таким образом, самая дешёвая покупка обойдётся в 2 400 руб. Ответ: 2400.
Ну вот, друзья, вы получили полезные знания о том, как покупать плитку и засеивать участок травой. Но мы пойдем дальше! Будем учиться строить бани!
2 тип. Бани
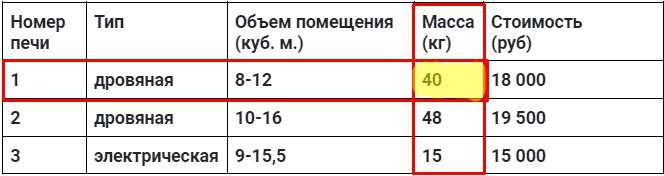
Хозяин дачного участка строит баню с парным отделением. Парное отделение имеет размеры: длина 3,5 м, ширина 2,2 м, высота 2 м. Окон в парном отделении нет, для доступа внутрь планируется дверь шириной 60 см, высота дверного проема 1,8 м. Для прогрева парного отделения можно использовать электрическую или дровяную печь. В таблице представлены характеристики трех печей.
| Номер печи | Тип | Объем помещения (куб. м.) | Масса (кг) | Стоимость (руб) |
| 1 | дровяная | 8-12 | 40 | 18 000 |
| 2 | дровяная | 10-16 | 48 | 19 500 |
| 3 | электрическая | 9-15,5 | 15 | 15 000 |
Для установки дровяной печи дополнительных затрат не потребуется. Установка электрической печи потребует подведения специального кабеля, что обойдется в 5700 руб.
Установите соответствие между массами и номерами печей. Заполните таблицу, в бланк ответов перенесите последовательность трех цифр без пробелов, запятых и других дополнительных символов.
| Масса (кг) | 15 | 40 | 48 |
| Номер печи | 3 | 1 | 2 |
Решение. Перечитаем еще раз условие задачи. Вся информация о массе печей есть в первой таблице, и нужно просто установить соответствие между столбцами и строками из таблицы.
Ищем печь с массой 15 кг – это печь номер 3.

Печь с массой 40 кг – печь с номером 1:
48 кг имеет печь под номером 2:

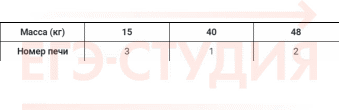
Найти суммарную площадь стен парного отделения строящейся бани (без площади двери). Ответ дайте в квадратных метрах.
Решение. Баня представляет из себя параллелепипед. Нарисуем схематично параллелепипед с указанием всех размеров (все значения берем из условия).
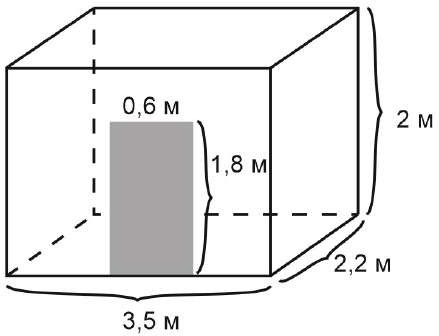
Теперь считаем площадь стен и вычитаем из нее площадь двери:
𝑆 = 2 ⋅ 2,2 + 2 ⋅ 2,2 + 2 ⋅ 3,5 + 2 ⋅ 3,5 − 0,6 ⋅ 1,8 =
= 2 ⋅ (2,2 + 2,2 + 3,5 + 3,5) −
Ответ: 21,72.
6 ⋅ 18

100
= 2 ⋅ 11,4 −
108

100
= 22,8 − 1,08 = 21,72
На сколько рублей покупка дровяной печи, подходящей по объему парного отделения, обойдется дешевле электрической с учетом установки?
Решение. Стоимость электрической печи известна из таблицы в условии (15 000 рублей и установка 5 700 руб, итого 15 000 + 5 700 = 20 700). Но стоимость деревянной печи… Указаны две стоимости, для разного объема.
| Номер печи | Тип | Объем помещения (куб. м.) | Масса (кг) | Стоимость (руб) |
| 1 | дровяная | 8-12 | 40 | 18 000 |
| 2 | дровяная | 10-16 | 48 | 19 500 |
| 3 | Электри- ческая | 9-15,5 | 15 | 15 000 |
Значит, сначала нужно узнать объем бани (чтобы оценить стоимость). Воспользуемся чертежом из задания 2. Объем параллелепипеда равен:
𝑉 = 3,5 ⋅ 2 ⋅ 2,2 = 7 ⋅ 2,2 = 15,4 ∈ [10; 16]
Значит, стоимость деревянной печи подходящего объема равна 19 500 руб. На сколько рублей покупка дровяной печи дешевле?
20 700 - 19 500 = 1 200.
Ответ: 1 200.
В прошлом году печи, указанные в таблице, стоили дороже. На них были сделаны скидки: на печь номер 1 скидка составила 10%, на печь номер 2
- 35%, на печь номер 3 - 25%. Сколько рублей стоила печь номер 1 в прошлом году?
Решение. Составим пропорцию.
На печь номер 1 скидка равна 10%, значит, сейчас ее стоимость составляет 100- 10 = 90%. А стоимость год назад (без скидки) - 100%.
90% = 18 000 руб
100% = х руб
 𝑥 = 18000 ⋅100 = 2000 ⋅ 10 = 20 000 руб.
𝑥 = 18000 ⋅100 = 2000 ⋅ 10 = 20 000 руб.
90
Ответ: 20 000.
Хозяин выбрал дровяную печь (рис.1). Чертеж передней панели печи показан на рисунке 2.
Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке печки по дуге окружности с центром в середине нижней части кожуха (рис.2). Для установки печки хозяину понадобилось узнать радиуса закругления арки R. Размеры кожуха в
сантиметрах показаны на рисунке. Найдите радиус закругления арки в сантиметрах.
Решение. Вновь отметим все, что известно из условия, на схеме (кстати, на ОГЭ можно рисовать на бланке — это удобно).
Нужно найти радиус - т.е. ВС. При этом мы знаем два катета в прямоугольном треугольнике АВС: АВ = 60 (по условию), а АС - это половина от 50 см, т.е. 25 (т.к. сказано “с центром в середине нижней части кожуха”).
Найдем гипотенузу по теореме Пифагора:
АВ2 + АС2 = ВС2
602 + 252 = 3600 + 625 = 4225 = 652
ВС = 65
Значит, радиус закругления равен 65. Ответ: 65.
Что там еще бывает на дачных участках? Теплицы! Обычно теплицы строят как придется: берут рейки, сколачивают каркас, натягивают полиэтилен. Сажают кабачки, а потом не знают, куда эти кабачки девать. Но составители заданий ЕГЭ применяют научный подход к постройке теплицы, и кабачки у них вырастают в 2 раза крупнее! : -)
3 тип. Теплицы

и при входе в теплицу будут дорожки шириной 40 см, для которых надо купить тротуарную плитку размером 20х20 см.
Юрий Борисович начал строить на 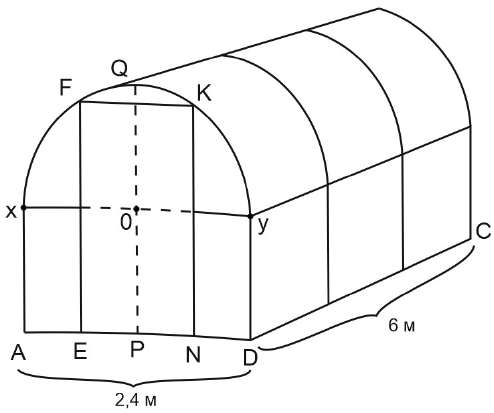 дачном участке теплицу (рис.1). Для этого он сделал прямоугольный фундамент длиной 6м (DC на рис.2) и шириной 2,4 м (AD на рис.2). Нижний ярус теплицы имеет форму прямоугольного параллелепипеда, собран из металлического профиля и по длине для прочности укреплен металлическими стойками. Высота нижнего яруса теплицы в два раза меньше ее ширины. Для верхнего яруса теплицы Юрий Борисович заказал металлические дуги в форме полуокружностей, которые крепятся к стойкам нижнего яруса. Отдельно требуется купить материал для обтяжки поверхности теплицы. В передней стенке планируется вход, показанный на рис.1 прямоугольником EFKN, где точки E, P и N делят отрезок AD на равные части. Внутри теплицы Юрий Борисович планирует сделать три грядки: одну широкую центральную и две одинаковые узкие по краям, как показано на рис.2. Между грядками
дачном участке теплицу (рис.1). Для этого он сделал прямоугольный фундамент длиной 6м (DC на рис.2) и шириной 2,4 м (AD на рис.2). Нижний ярус теплицы имеет форму прямоугольного параллелепипеда, собран из металлического профиля и по длине для прочности укреплен металлическими стойками. Высота нижнего яруса теплицы в два раза меньше ее ширины. Для верхнего яруса теплицы Юрий Борисович заказал металлические дуги в форме полуокружностей, которые крепятся к стойкам нижнего яруса. Отдельно требуется купить материал для обтяжки поверхности теплицы. В передней стенке планируется вход, показанный на рис.1 прямоугольником EFKN, где точки E, P и N делят отрезок AD на равные части. Внутри теплицы Юрий Борисович планирует сделать три грядки: одну широкую центральную и две одинаковые узкие по краям, как показано на рис.2. Между грядками
Найдите высоту теплицы PQ в метрах
Решение. Классическая геометрическая задача. Для удобства обозначим дополнительно три точки на чертеже: Х, О и У.

Высота PQ = PO + QO
Про высоту РО в условии сказано “высота нижнего яруса теплицы в два раза меньше ее ширины”. Ширина равна 2,4м, значит, PO = 1,2м.
QO = XO = YO = R полуокружности. Т.к. ХУ = 2,4 — это диаметр полуокружности, то R = 1,2.
Итого: PQ = PO + QO = 1,2 + 1,2 = 2,4 м.
Ответ: 2,4.
Сколько нужно купить упаковок плитки для дорожек, если в каждой упаковке 6 штук?
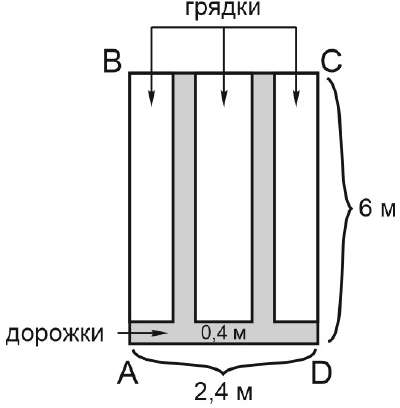
Решение. Посчитаем в метрах длину всех дорожек: 2 ⋅ 6 + 2,4 − 0,4 − 0,4 = 13,6м
(почему вычитаем два раза по 0,4 м? потому что иначе оранжевые квадраты на рисунке ниже были бы учтены два раза)
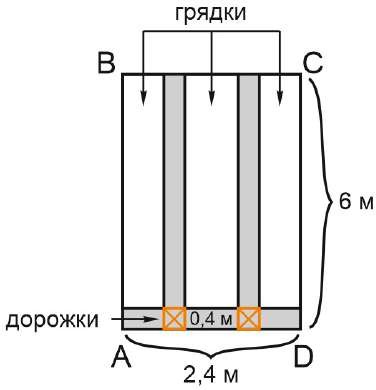
Кстати, можно было посчитать и по-другому. Например, вертикальные дорожки считать не по 6м, а по 6-0,4=5,6 м. Тогда общая длина была бы равна: 2 ⋅ 5,6 + 2,4 = 11,2 + 2,4 = 13,6. Посчитали двумя способами, и результат сошелся — значит, мы на правильном пути.
13,6 : 0,2 = 68 раз помещается одна плитка по всей длине. При этом в одном ряду будет не 1 плитка, а 2 (т.к. ширина дорожки 40 см, а ширина плитки 20 см). Значит, всего понадобится плиток: 68 ⋅ 2 = 136.
Остается узнать, сколько упаковок нужно купить, если в упаковке 6 штук.
136 : 6 = 222
3
 Поскольку в магазине никто не продаст 2
Поскольку в магазине никто не продаст 2
3
упаковки плитки, значит, придется брать
целую. Итого получится 23 упаковки. Ответ: 23.
Найдите ширину центральной грядки, если она в 1,2 раза больше ширины узкой грядки. Ответ дайте в сантиметрах.
Решение.
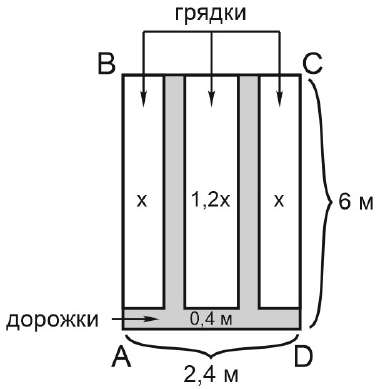
Составим уравнение:
𝑥 + 0,4 + 1,2𝑥 + 0,4 + 𝑥 = 2,4
𝑥 = 0,5
1,2𝑥 = 1,2 ⋅ 0,5 = 0,6м = 60см
Ответ: 60
Найдите длину металлической дуги для верхнего яруса теплицы. Ответ дайте в метрах, округлив его в большую сторону с точностью до десятых.
Решение. Длина металлической дуги для верхнего яруса теплицы — это половина длины окружности с радиусом R=1,2м (радиус знаем из задания 1)
Ответ: 3,8
𝐿 =
1
 2𝜋𝑅 = 𝜋𝑅 ≈ 3,14 ⋅ 1,2 = 3,768 ≈ 3,8
2𝜋𝑅 = 𝜋𝑅 ≈ 3,14 ⋅ 1,2 = 3,768 ≈ 3,8
2
Найдите высоту EF входа в теплицу в сантиметрах с точностью до целого.
Решение. Высота EF = FM + ME
ME = 1,2м = 120 см (знаем из задания 1).
Найдем FM из прямоугольного треугольника OFM (в котором OF = 1,2 = R,
 2,4 = 0,6м = 60 см.
2,4 = 0,6м = 60 см.
4
𝑂𝑀 =
 1 𝐴𝐷 =
1 𝐴𝐷 =
4
По теореме Пифагора:
𝑂𝐹2 = 𝑂𝑀2 + 𝐹𝑀2
1202 = 𝑂𝑀2 + 602

𝑂𝑀 = 60√3 ≈ 60 ⋅ 1,7 = 102см
EF= 120+102 = 222 см.
 *Внимательный ученик в этом месте может засомневаться насчет того, а что, если его ответ после округления не попадет в правильный. Ведь 𝜋 можно взять не 3,14, а точнее. И √3 тоже можно округлить не как 1,7. Что тогда делать?
*Внимательный ученик в этом месте может засомневаться насчет того, а что, если его ответ после округления не попадет в правильный. Ведь 𝜋 можно взять не 3,14, а точнее. И √3 тоже можно округлить не как 1,7. Что тогда делать?
Хорошая новость в том, что разработчики заданий это учли. И даже если в решении вы возьмете более точные значения приближенных чисел и у вас получится немного другой ответ (например, 223) - его зачтут. Поэтому в задании 5 правильным ответом является любое из чисел: 222, 223, 224, 225.
Ответ: 222 см.
Так, дачный участок обустроили, пора в офис на работу. Знаете ли вы, почему стандартный лист офисной бумаги А4 имеет размеры 297 на 210 миллиметров? Почему не 300 на 200?
Ответ вы прочитаете в условии следующей задачи. А мы его прокомментируем.
4 тип. Листы бумаги
Общепринятые форматы листов бумаги обозначают буквой А и цифрой: А0, А1, А2 и так далее. Площадь листа формата А0 равна 1 кв.м. Если лист формата А0 разрезать пополам параллельно меньшей стороне, получаются два листа формата А1. Если так же лист А1 разрезать пополам, получаются два листа формата А2 и так далее.
Отношение длины листа к его ширине у всех форматов, обозначенных буквой А, должно быть одно и то же, то есть листы должны быть подобны друг другу. Это сделано специально, чтобы можно было сохранить пропорции текста на листе при изменении формата бумаги (размер шрифта при этом тоже соответственно изменится. На практике размеры листа округляют до целого числа миллиметров.
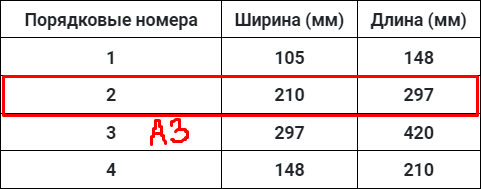
В таблице 1 даны размеры листов бумаги четырех размеров: от А3 до А6.
| Порядковые номера | Ширина (мм) | Длина (мм) |
| 1 | 105 | 148 |
| 2 | 210 | 297 |
| 3 | 297 | 420 |
| 4 | 148 | 210 |
Для листов бумаги форматов А3, А4, А5 и А6 определите, какими порядковыми номерами обозначены их размеры в таблице 1. Заполните таблицу ниже, в бланк ответов перенесите последовательность четырех цифр.
| Форматы бумаги | А3 | А4 | А5 | А6 |
| Порядковые номера |
|
|
|
|
Решение. Самое время разобраться с условием.
Чем меньше цифра, тем больше размер листа. Поэтому А0 - самый большой лист, А1 - в 2 раза меньше по площади, А2 - в 4 раза меньше по площади, и т.д.
Т.к. в таблице указаны форматы от А3 до А6, то самый большой размер листа будет у формата с наименьшей порядковой цифрой (т.е. у А3). Найдем лист с самыми большими размерами. Это лист 297х420 под порядковым номером 3. Значит, А3 имеет порядковый номер 3.
Теперь алгоритм поиска А4 простой: берем бОльшую сторону, делим ее пополам, а вторую сторону оставляем без изменений.
Большая сторона = 420, делим ее пополам, получаем: 420 : 2 = 210. А сторону 297 мм оставляем без изменений.
Ищем в таблице лист с размерами 210 и 297 мм для формата А4. Это порядковый номер 2.
Вновь повторяем алгоритм для нахождения формата А5. БОльшая сторона листа А4 = 297, меньшая сторона = 210.
297 ∶ 2 = 148,5 ∼ 148
Ищем строку с параметрами 210 и 148 мм. Это порядковый номер 4 в таблице.
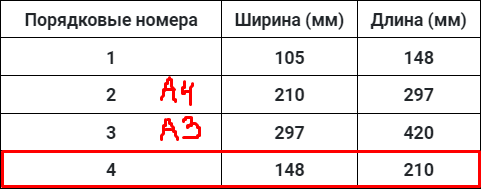
Логично предположить, что единственный оставшийся порядковый номер 1 принадлежит формату А6. Но можно по расчетам убедиться, что до этого мы все делали правильно – зачем терять такую возможность самопроверки? Поэтому продолжим алгоритм:
Большая сторона равна 210, меньшая 148.
210 : 2 = 105.

Значит, формат А6 должен иметь параметры 105 и 148. А это как раз данные первой строки. То есть до этого все сделано правильно.
Заносив таблицу из условия полученные значения:
В бланк ответа на ОГЭ запишем: 3241. Ответ: 3241.
Сколько листов бумаги формата А5 получится при разрезании одного листа бумаги формата А0?
Решение. Из одного листа А0 получается два листа А1, А0 = 2А1
Из одного листа А1 получается два листа А2, т.е. А0 = 2А1 = 2 ⋅ 2А2 = 4А2
Из одного листа А2 получается два листа А3, А0 = 2А1 = 2 ⋅ 2А2 = 4А2 = 4 ⋅ 2А3 = 8А3
По аналогии, А0 = 8А3 = 8 ⋅ 2А4 = 16А4 = 16 ⋅ 2А5 = 32А5
Значит, из одного листа А0 получается 32 листа А5. Ответ: 32.
Найдите длину большей стороны листа бумаги формата А2. Ответ дайте в миллиметрах.
Решение. Чтобы узнать размеры листа бумаги формата А2, нужно знать размеры соседних форматов: А1 или А3.
При решении данной задачи размеры листа А1 нам не встречались. А вот размеры А3 мы знаем из решения задания 1: 297мм х 420 мм.
Вспомним, как мы решали задание 1 (находили меньший формат листа, зная бОльший): берем бОльшую сторону, делим ее пополам, а вторую сторону оставляем без изменений.
Значит, чтоб получить бОльший формат из меньшего, поступаем наоборот: берем меньшую сторону, умножаем ее на два, а вторую сторону оставляем без изменений.
Меньшая сторона в размере А3 297х420 равна 297.
297 ⋅ 2 = 594. Тогда размер А2: 594х420. БОльшая сторона = 594.
Ответ: 594.
Найдите площадь листа бумаги формата А3. Ответ дайте в квадратных сантиметрах.
Решение. Площадь листа А3 - это площадь прямоугольника. Опять воспользуемся данными из задания 1:
Лист А3 имеет размеры 297мм х 420мм.
Можно найти площадь в миллиметрах. Но поскольку ответ нужно дать в квадратных сантиметрах, то сразу посчитаем площадь в квадратных сантиметрах.
297 мм = 29,7 см
420 мм = 42 см
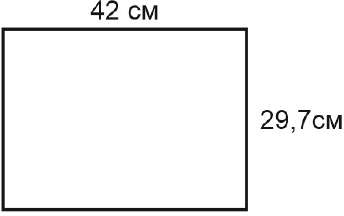
𝑆 = 42 ⋅ 29,7 = 1247,4
Ответ: 1247,4
Бумагу формата А5 упаковали в пачки по 500 листов. Найдите массу пачки, если масса бумаги площадью 1 кв.м равна 80 г. Ответ дайте в граммах.
Решение. В условии сказано, что “Площадь листа формата А0 равна 1 кв.м”.
При этом из задания 2 мы уже знаем, что из 1 листа А0 получится 32 листа формата А5.
Значит, 32 листа А5 по площади равны 1 кв.м, а масса бумаги площадью 1 кв.м равна 80 г.
Составим пропорцию:
32 листа = 80 г 500 листов = х
 𝑥 = 500⋅80 = 1250г
𝑥 = 500⋅80 = 1250г
32
Ответ: 1250.
Почему же у листа бумаги А4 размеры 297 на 210? Дело в том, что длина этого листа в √2 раз больше, чем его ширина. Это необходимо для того, чтобы при делении такого листа пополам получался лист, подобный данному, то есть с такими же пропорциями, но вдвое меньший по площади.
А теперь – Те Самые Шины. Сейчас вы узнаете о шинах больше, чем ваши родители! Если, конечно, они не работают на шинном заводе. Что там написано на колесе у грузовика, давайте разберемся.
5 тип. Шины
Автомобильное колесо, как правило, представляет из себя металлический диск с установленной на него резиновой шиной. Диаметр диска совпадает с диаметром внутреннего отверстия в шине.
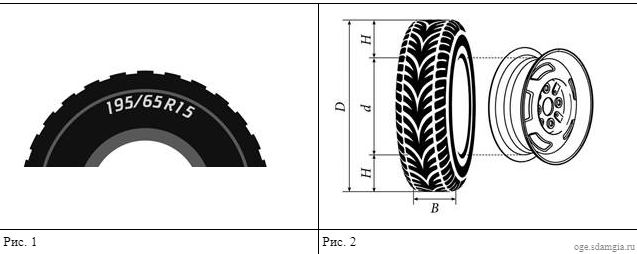
Для маркировки автомобильных шин применяется единая система обозначений. Например, 195/65 R15 (рис.1). Первое число (число 195 в приведенном примере) обозначает ширину шины в миллиметрах (параметр В на рисунке 2). Второе число (число 65 в приведенном примере) - процентное отношение высоты
 боковины (параметр Н на рисунке 2) к ширине шины, т.е. 100 ⋅ 𝐻𝐻.
боковины (параметр Н на рисунке 2) к ширине шины, т.е. 100 ⋅ 𝐻𝐻.
𝐵
Последующая буква обозначает тип конструкции шины. В данном примере буква R означает, что шина радиальная, то есть нити каркаса в боковине шины расположены вдоль радиусов колеса. На всех легковых автомобилях применяют шины радиальной конструкции.
За обозначением типа конструкции шины идет число, указывающее диаметр диска колеса d в дюймах (в одном дюйме 25,4 мм). Таким образом, общий диаметр колеса D легко найти, зная диаметр диска и высоту боковины.
Возможны дополнительные маркировки, обозначающие допустимую нагрузку на шину, сезонность использования, тип дорожного покрытия и другие параметры.
Завод производит внедорожники определенной модели и устанавливает на них колеса с шинами маркировки 265/60 R18.
Прежде, чем читать вопросы к данной задаче, давайте разберемся, что дано по условию, если мы знаем маркировку шины.
На самом деле будет гораздо понятнее, если длинное условие переписать в виде формул:
Шины какой наибольшей ширины можно устанавливать на автомобиль, если диаметр диска равен 17 дюймам? Ответ дайте в миллиметрах.
Решение. Задание, в котором нужно прочитать условие и посмотреть на таблицу:
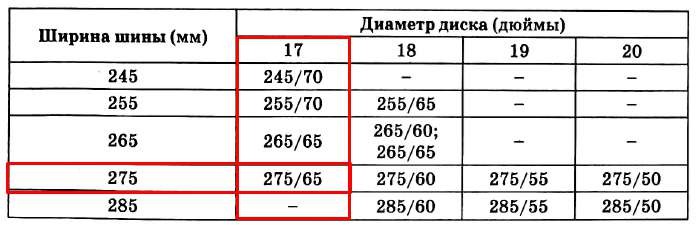
Ответ: 275
На сколько миллиметров радиус колеса с шиной маркировки 245/70 R17 меньше, чем радиус колеса с шиной маркировки 275/65 R17?
 Решение. Радиус колеса неизвестен. При этом формула диаметра дана по условию (на рис.2): 𝐷 = 𝑑𝑑 + 2𝐻
Решение. Радиус колеса неизвестен. При этом формула диаметра дана по условию (на рис.2): 𝐷 = 𝑑𝑑 + 2𝐻
Значит,
𝑅 =
𝑑𝑑 2
+ 𝐻
Т.к. d=17 дюймов для обоих колес, то разница между радиусами - это разница между H. Поэтому найдем величину Н для каждого колеса.
245/70 R17
Воспользуемся формулами, которые мы вывели из условия: В = 245,
 𝐻 = 245⋅70 = 171,5 (мм)
𝐻 = 245⋅70 = 171,5 (мм)
100
100 ⋅ Н

245
= 70
𝑅1
= 17⋅25,4 + 171,5 (мм)
 2
2
275/65 R17 В=275
100 ⋅ 𝐻

275
= 65
 𝐻 = 275⋅65 = 178,75 (мм)
𝐻 = 275⋅65 = 178,75 (мм)
100
𝑅2
= 17⋅25,4 + 178,75 (мм)
 2
2
Находим разницу между радиусами:
𝑅2 − 𝑅1 =
Ответ: 7,25.
17 ⋅ 25,4
 + 178,75 −
+ 178,75 −
2
17 ⋅ 25,4
 − 171,5 = 178,75 − 171,5 = 7,25
− 171,5 = 178,75 − 171,5 = 7,25
2
Найдите диаметр колеса автомобиля, выходящего с завода. Ответ дайте в миллиметрах
Решение. С завода выходят колеса с шинами маркировки 265/60 R18. Рассчитаем диаметр D
𝐵 = 265
 𝐻 = 60⋅265 = 159 (мм)
𝐻 = 60⋅265 = 159 (мм)
100
𝐷 = 18 ⋅ 25,4 + 2 ⋅ 159 = 775,2 (мм)
Ответ: 775,2.
100 ⋅ 𝐻

265
= 60
На сколько миллиметров увеличится диаметр колеса, если заменить колеса, установленные на заводе, колесами с шинами маркировки 285/50 R20?
Решение. Диаметр исходных шин мы нашли в задании 3. Повторим все вычисления диаметра для новой маркировки шин.
𝐵 = 285
100 ⋅ 𝐻

285
= 50
𝐻 =
50 ⋅ 285

100
= 142,5
= 20 ⋅ 25,4 + 2 ⋅ 142,5 = 793 (мм)
Разница между диаметрами: 793 − 775,2 = 17,8
Ответ: 17,8.
Кирилл планирует заменить зимнюю резину на летнюю на своем автомобиле. Для каждого из четырех колес последовательно выполняются четыре операции: снятие колеса, замена шины, балансировка колеса и установка колеса. Он выбирает между автосервисами А и Б. Затраты на дорогу и стоимость операций даны в таблице
Сколько рублей заплатит Кирилл за замену резины на своем автомобиле, если выберет самый дешевый вариант?)
Решение. Наконец, простые вычисления без специальных формул.
Суммарные затраты на дорогу не зависят от количества колес, а снятие, замена, балансировка и установка - рассчитываются на каждое колесо.
Получаем:
𝐴 = 270 + 4 ⋅ (57 + 235 + 215 + 57) = 270 + 2256 = 2526
𝐵 = 450 + 4 ⋅ (52 + 205 + 195 + 52) = 450 + 2016 = 2466
2466 2526, значит, ответ: 2466.
Ответ: 2466.
Мы сделали это! Разобрали самую запутанную из всех типов задач 1-5 ОГЭ. Что пишут на колесах автомобиля, мы теперь знаем. Но составители заданий ОГЭ на этом не успокоились! Автомобиль надо еще и застраховать.

1








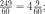



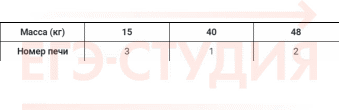



 𝑥 = 18000 ⋅100 = 2000 ⋅ 10 = 20 000 руб.
𝑥 = 18000 ⋅100 = 2000 ⋅ 10 = 20 000 руб.
 дачном участке теплицу (рис.1). Для этого он сделал прямоугольный фундамент длиной 6м (DC на рис.2) и шириной 2,4 м (AD на рис.2). Нижний ярус теплицы имеет форму прямоугольного параллелепипеда, собран из металлического профиля и по длине для прочности укреплен металлическими стойками. Высота нижнего яруса теплицы в два раза меньше ее ширины. Для верхнего яруса теплицы Юрий Борисович заказал металлические дуги в форме полуокружностей, которые крепятся к стойкам нижнего яруса. Отдельно требуется купить материал для обтяжки поверхности теплицы. В передней стенке планируется вход, показанный на рис.1 прямоугольником EFKN, где точки E, P и N делят отрезок AD на равные части. Внутри теплицы Юрий Борисович планирует сделать три грядки: одну широкую центральную и две одинаковые узкие по краям, как показано на рис.2. Между грядками
дачном участке теплицу (рис.1). Для этого он сделал прямоугольный фундамент длиной 6м (DC на рис.2) и шириной 2,4 м (AD на рис.2). Нижний ярус теплицы имеет форму прямоугольного параллелепипеда, собран из металлического профиля и по длине для прочности укреплен металлическими стойками. Высота нижнего яруса теплицы в два раза меньше ее ширины. Для верхнего яруса теплицы Юрий Борисович заказал металлические дуги в форме полуокружностей, которые крепятся к стойкам нижнего яруса. Отдельно требуется купить материал для обтяжки поверхности теплицы. В передней стенке планируется вход, показанный на рис.1 прямоугольником EFKN, где точки E, P и N делят отрезок AD на равные части. Внутри теплицы Юрий Борисович планирует сделать три грядки: одну широкую центральную и две одинаковые узкие по краям, как показано на рис.2. Между грядками 

 Поскольку в магазине никто не продаст 2
Поскольку в магазине никто не продаст 2
 2,4 = 0,6м = 60 см.
2,4 = 0,6м = 60 см.




 𝑥 = 500⋅80 = 1250г
𝑥 = 500⋅80 = 1250г
 боковины (параметр Н на рисунке 2) к ширине шины, т.е. 100 ⋅ 𝐻𝐻.
боковины (параметр Н на рисунке 2) к ширине шины, т.е. 100 ⋅ 𝐻𝐻.
 Решение. Радиус колеса неизвестен. При этом формула диаметра дана по условию (на рис.2): 𝐷 = 𝑑𝑑 + 2𝐻
Решение. Радиус колеса неизвестен. При этом формула диаметра дана по условию (на рис.2): 𝐷 = 𝑑𝑑 + 2𝐻

 + 178,75 −
+ 178,75 − − 171,5 = 178,75 − 171,5 = 7,25
− 171,5 = 178,75 − 171,5 = 7,25











