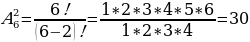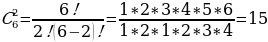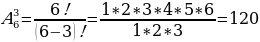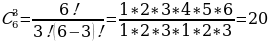План-конспект урока по дисциплине Математика на тему: "Подсчет числа размещений, перестановок, сочетаний"

Министерство образования, науки и молодежи Республики Крым

Государственное бюджетное профессиональное образовательное учреждение

«Красногвардейский агропромышленный техникум»

Методическая разработка урока

по предмету Математика

для обучающихся II курса.

Тема: «Подсчет числа размещений, перестановок, сочетаний».

Разработал преподаватель математики

Шерстобитова Вероника Андреевна

2022 г.

Тема: «Подсчет числа размещений, перестановок, сочетаний».

Цели:

Образовательные: отработать навыки вычисления размещения, перестановки и сочетания; научиться распознавать задачи на нахождение размещений, перестановок, сочетаний; решить простейшие комбинаторные задачи с помощью этих формул.

Воспитательные: формировать у обучающихся культуру математической речи, информационную и коммуникативную культуру, логическое мышление, умение применять знания в изменённой ситуации.

Развивающие: развивать познавательный интерес студентов, развивать умения сравнивать, систематизировать, обобщать полученные знания.

Тип занятия: комбинированный урок.

Инструменты и оборудование: рабочие тетради, доска и мел, учебник Алгебра и начала математического анализа 10 класс под редакцией С.М.Никольского.

Структура урока:

1) Организационный этап.

2) Постановка цели и задач урока. Мотивация учебной деятельности обучающихся.

3) Актуализация знаний.

4) Усвоение новых знаний.

5) Закрепление.

6) Информация о домашнем задании, инструктаж по его выполнению.

7) Рефлексия (подведение итогов занятия)

Ход урока:

1) Организационный этап: приветствие; отметить отсутствующих.

2) Постановка цели и задач урока.

На прошлом занятии мы научились вычислять вычислять размещения, перестановки и сочетания. Сегодня научимся применять полученные знания для решения задач из курса Теории вероятностей.

3) Актуализация знаний.

1. Что называют факториалом? (произведение натуральных чисел от 1 до n, обозначают n!)

2. Что называют перестановкой? (расположение элементов в определенном порядке, количество перестановок вычисляется по формуле ).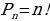

3. Что называют размещением? (любой упорядоченный набок k элементов, составленный из n элементов, вычисляют ).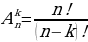

4. Что называют сочетанием? (любую группу из k элементов, составленную из n элементов, вычисляют ).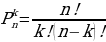

4) Усвоение новых знаний.

Давайте здороваться, т.е. все пожмем друг другу руки. Рядом сидящим пожмем руку, а с остальными будем здороваться мысленным  рукопожатием.

Вопрос: Сколько было всего рукопожатий?

Допустим нас 25.

Каждый из 25-и  человек пожал руки 24-м. Однако произведение 25 * 24 = 600 дает удвоенное число рукопожатий (так как в этом расчете учтено, что первый пожал руку второму, а затем второй первому, на самом же деле было одно рукопожатие). Итак, число рукопожатий равно: (25 * 24) : 2 = 300.

– Мы с вами столкнулись с комбинаторной задачей.   
Поиском ответов на вопросы: сколько всего есть комбинаций в том или другом случае, занят целый раздел математики, и мы познакомимся с ним. Особая примета подобных задач – это  вопрос, который   можно сформулировать таким образом, что он начинался бы словами:

• Сколькими способами…?

• Сколько вариантов…?

Комбинаторикой называют область математики, которая изучает вопросы о числе различных комбинаций (удовлетворяющих тем или иным условиям), которые можно составить из данных элементов.

В чем же отличия между размещениями, перестановками, сочетаниями спросите вы? Давайте разбираться.

Перестановки - соединения, которые можно составить из n предметов, меняя всеми возможными способами их порядок.

Размещения - соединения, содержащие по k предметов из числа n данных, различающиеся либо порядком предметов, либо самими предметами.

Сочетания - соединения, содержащие по k предметов из n, различающиеся друг от друга, по крайней мере, одним предметом.

Рассмотрим задачи:

З1. Сколько вариантов различных 3техзначных чисел можно составить из цифр 2, 5, 8 без повторения данных цифр в числе?

- на первое место мы можем поставить любую цифру из трех;

- на второе место мы можем поставить любую цифру, но уже из двух оставшихся, ведь оду цифру мы уже поставили на первое место;

-ну и на третье место мы можем поставить последнюю не задействованную цифру.

Тогда количество перестановок будет равно 3*2*1=6. Давайте попробуем составить все возможные числа, чтоб проверить правильность наших расчетов: 258, 285, 528, 582, 825, 852. Других чисел без повторения составить не получится.

Ответ: всего 6 трехзначных чисел.

З2. Рассмотрим похожую задачу. Сколько вариантов различных трехзначных чисел можно составить из цифр 2, 5, 8 если допускается повторения данных цифр в числе?

На любое место в трехзначном числе мы можем поставить любую из трех цифр. Значит количество вариантов 3*3*3=27. Обучающимся предлагается составить все перестановки и убедиться в правильности вычислений.

Ответ: 27 трехзначных чисел

№1.60 (а) стр.27 Сколькими различными способами можно распределить между 6 лицами 2 различные путевки в санатории?

Обратим внимание, что разным людям предлагают путевки в разные санатории. Когда важен порядок, в таких случаях и используют размещения.

Людей 6, путевок 2. И имеет значение Иванов поедет в санаторий Чайка или Радуга.

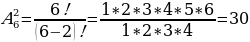
Ответ: 30 способами.

З3. Изменим условие. Сколькими различными способами можно распределить между 6 лицами 2 путевки в один санаторий?

Обратим внимание, что разным людям предлагают путевки в один санатории. Т.е. не важно Иванову предложат путевку №1 или №2, они ведь одинаковые. Когда не важен порядок, в таких случаях и используют сочетания.

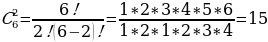
Ответ: 15 способами.

5) Закрепление.

З4. Сколько вариантов различных 3техзначных чисел можно составить из цифр 2, 5, 8, 9, 0 без повторения данных цифр в числе; если допускаются повторения?

Обучающимся предлагается самостоятельно выполнить данную задачу

5*4*3=60

5*5*5=125

Ответ: 60 трехзначных чисел без повторения цифр, 125 трехзначных чисел если учитывать с повторяющимися цифрами.

№1.60(б) стр.27

Решение:

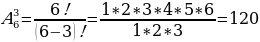
Ответ: 120 способами.

№1.66 стр.29

Решение:

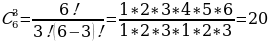
Ответ: 20 способами.

6) Информация о домашнем задании, инструктаж по его выполнению.

№1.60 (а) стр.27, №1.67 стр.29.

7) Рефлексия (подведение итогов занятия).

- что называют перестановками?

-в чем заключаются отличия между размещениями и перестановками?

-Метопредметные связи:

Как вы думаете в каких областях еще можно применять знания, поученные на сегодняшнем уроке?

• учебные заведения (составление расписаний)

• сфера общественного питания (составление меню)

• лингвистика (рассмотрение вариантов комбинаций букв)

• география (раскраска карт)

• спортивные соревнования (расчёт количества игр между участниками)

• производство (распределение нескольких видов работ между рабочими)

• агротехника (размещение посевов на нескольких полях)

• азартные игры (подсчёт частоты выигрышей)

• химия (анализ возможных связей между химическими элементами)

• экономика (анализ вариантов купли-продажи акций)

• криптография (разработка методов шифрования)

• доставка почты (рассмотрение вариантов пересылки)
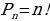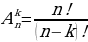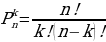