Пояснительная записка

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА.

Рабочая программа по математике в 9 - б классе составлена на основе следующих нормативно-правовых документов:

1. Федерального Закона «Об образовании в Российской Федерации» (от 29.12. 2012 № 273-ФЗ).

2. Постановления Главного государственного санитарного врача РФ от 6 марта 1986 г. N 4076-86 «Санитарные правила, устройства, оборудования, содержания и режима специальных общеобразовательных школ-интернатов для детей, имеющих недостатки в физическом и умственном развитии».

3. Постановления Главного государственного санитарного врача РФ от 29.12.2010 № 189 «Об утверждении СанПиН 2.4.2.2821-10 «Санитарно-эпидемиологичес-кие требования к условиям и организации обучения в общеобразовательных учреждениях».

4. Приказа Минобразования РФ от 10 апреля 2002 года № 29/2065-п «Об утверждении учебных планов специальных (коррекционных) образовательных учреждений для обучающихся, воспитанников с отклонениями в развитии».

5. Приказа Минобрнауки России от 19.12.2012 № 1067 «Об утверждении федеральных перечней учебников, рекомендованных (допущенных) к использованию в образовательном процессе в образовательных учреждениях, реализующих образовательные программы общего образования и имеющих государственную аккредитацию, на 2013-2014 учебный год».

6. Приказа Минобрнауки России от 31 марта 2014 г. «Об утверждении федерального перечня учебников, рекомендуемых к использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего образования».

7. Приказа Минобразования Ростовской области от 14.07.2011 № 610 «Об утверждении примерного регионального положения о рабочей программе курсов, предметов, дисциплин (модулей)» (Приложение).

8. Письма Минобразования Ростовской области от 08.08.2014 №24/4.1.1-4851/м «О примерном порядке утверждения и примерной структуре рабочей программы учебных курсов, предметов, дисциплин (модулей) (Приложение 1).

9. Положения о рабочей программе ГКОУ РО Азовской школы-интерната № 10.

10. Устава ГКОУ РО Азовской школы-интерната № 10.

11. Учебного плана ГКОУ РО Азовской школы-интерната №10 на 2015 – 2016 учебный год.

Для обеспечения учебного процесса в 9-б классе примерная программа основного общего образования по алгебре и авторская программа по алгебре взяты из методического пособия «Программы общеобразовательных учреждений» АЛГЕБРА 7-9 классы, составитель: Бурмистрова Т.А., издательство «Просвещение», 2008 г. Для обеспечения учебного процесса в 9-бклассе примерная программа основного общего образования по геометрии и авторская программа по геометрии взяты из методического пособия «Программы общеобразовательных учреждений» ГЕОМЕТРИЯ 7-9 классы, составитель: Бурмистрова Т.А., издательство «Просвещение», 2010

Рабочая программа по курсу математики в 9-б классе составлена для УМК Г.В. До­рофеев, С.Б.Суворова, Е.А. Бунимович и др «Алгебра 7» (М.: Просвещение,2005-2007), и УМК Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. «Геометрия 7-9» (М.: Просвещение, 2004-2008), включённых в Федеральный перечень учебников на 2015-2016 учебный год.

Общая характеристика предмета

Математика является одним из основных системообразующих предметов школьного образования. Такое место математики среди школьных предметов обусловливает и ее особую роль с точки зрения всестороннего развития личности учащихся. Обучение математике является важнейшей составляющей основного общего образования и призвано развивать логическое мышление и математическую интуицию учащихся, обеспечить овладение учащимися умениями в решении различных практи­ческих и межпредметных задач.

В основе содержания обучения математике лежит овладение учащимися следующими видами компетенций: предметной, коммуникативной, организационной и общекультурной.

Под предметной компетенцией понимается осведомлённость школьников о системе основ­ных математических представлений и овладение ими необходимыми предметными умениями. Формируются следующие образующие эту компетенцию представления: о математическом языке как сред­стве выражения математических законов, закономерностей и т.д.; о математическом моделировании как одном из важных методов познания мира. Формируются следующие образующие эту компетенцию умения: создавать простейшие математические модели, работать с ними и интерпретировать по­лученные результаты; приобретать и систематизировать знания о способах решения математических задач, а также применять эти знания и умения для решения многих жизненных задач.

Под коммуникативной компетенцией понимается сформированность умения ясно и чётко излагать свои мысли, строить аргументированные рассуждения, вести диалог, воспринимая точку зре­ния собеседника и в то же время подвергая её критическому анализу, отстаивать (при необходимости) свою точку зрения, выстраивая систему аргументации. Формируются образующие эту компетенцию умения, а также умения извлекать информацию из разного рода источников, преобразовывая её при необходимости в другие формы (тексты, таблицы, схемы и т.д.).

Под организационной компетенцией понимается сформированность умения самостоятельно находить и присваивать необходимые учащимся новые знания. Формируются следующие образующие эту компетенцию умения: самостоятельно ставить учебную задачу (цель), разбивать её на составные части, на которых будет основываться процесс её решения, анализировать результат действия, выяв­лять допущенные ошибки и неточности, исправлять их и представлять полученный результат в форме, легко доступной для восприятия других людей.

Под общекультурной компетенцией понимается осведомленность школьников о математике как элементе общечеловеческой культуры, её месте в системе других наук, а также её роли в развитии представлений человечества о целостной картине мира. Формируются следующие образующие эту компетенцию представления: об уровне развития математики на разных исторических этапах; о высо­кой практической значимости математики с точки зрения создания и развития материальной культуры человечества, а также о важной роли математики с точки зрения формировании таких важнейших черт личности, как независимость и критичность мышления, воля и настойчивость в достижении цели и др.

Ведущей идеей современной концепции школьного образования является идея гуманизации, ста­вящая в центр процесса обучения ученика с его интересами и возможностями, тре­бующая учета осо­бенностей его личности. Такая позиция определяет общие направле­ния пе­рестройки школьного мате­матического образования, главными из которых являются усиление общекультурного звучания курса и повышение его значимости для формирования личности подрастающего человека.

Основной целью изучения математики является формирование математического стиля мыш­ления, проявляющегося в определенных умственных навыках, способствующего форми­рованию алгоритмического мышления, воспитании умений действовать по задан­ному алгоритму и конструиро­вать новые. Главной целью школьного образования является развитие ребенка как компетентной личности путем включения его в различные виды ценностной человеческой деятельности: учеба, познания, коммуникация, профессионально-трудовой выбор, личностное саморазвитие, ценностные ориентации, поиск смыслов жизнедеятельности. С этих позиций обучение рассматривается как процесс овладения не только определенной суммой знаний и системой соответствующих умений и навыков, но и как процесс овладения компетенциями. Это определило задачи обучения математики:

• овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;

• интеллектуальное развитие обучающихся, и прежде всего таких его компонентов, как ин­тел­лекту­альная восприимчивость, способность к усвоению новой информации, под­виж­ность, гиб­кость и независимость мышления;

• создание широкого круга математических представлений и одновременно отказ от формирования некоторых специальных математических умений;

• перенос акцентов с формального на содержательное, развитие понятий и утверждений на наглядной основе, повышение роли интуиции и воображения как основы для фор­мирова­ния математиче­ского мышления и интеллектуальных способностей;

• формирование личностно-ценностного отношения к математическим знаниям, представ­ле­ния о математике как части общечеловеческой культуры, усиление практического аспекта в преподавании, развитие умения применять математику в реальной жизни;

Ценностные ориентиры

Содержание программы по математике направлено на освоение обучающимися базовых знаний и формированию базовых компетентностей, что способствует требованиям образовательной программы основного общего образования ГКОУ Азовской школы – интерната №10, рабочая программа включают все темы, предусмотренные для изучения федерального государственного стандарта общего образования по алгебре и геометрии . В основе построения данной программы лежит идея гуманизации обучения, соответствующая современным представлениям о целях школьного образования и уделяющая особое внимание лично­сти ученика, его интересам и способностям. Это позволяет обеспечить формирование как предметных умений, так и универсальных учебных действий школьников, а также способствует достижению опре­делённых во ФГОС личностных результатов, которые в дальнейшем позволят учащимся применять полученные знания и умения для решения различных жизненных задач.

Курс математики 7-го класса разделяется на изучение алгебры и геометрии. Геометрия — один из важнейших компонентов математического образования, необходимый для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, для эстетического воспитания учащихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства. На уроках геометрии расширяются сведения о геометрических фигурах. На начальном этапе основное внимание уделяется двум аспектам: понятию равенства геометрических фигур (отрезков и углов) и свойствами измерения отрезков и углов. Главное место занимают признаки равенства треугольников. Формируются умения выделять равенство трех соответствующих элементов данных треугольников и делать ссылки на изученные признаки. Особое внимание уделяется доказательству параллельности прямых с использованием соответствующих признаков. Теорема о сумме углов треугольника позволяет получить важные следствия, что существенно расширяет класс решаемых задач. Серьезное внимание уделяется формированию умений рассуждать, делать простые доказательства, давать обоснования выполняемых действий.

Курс геометрии характеризуется рациональным сочетанием логической строгости и геометрической наглядности. Увеличивается теоретическая значимость изучаемого материала; расширяются внутренние логические связи курса; повышается роль дедукции, степень абстрактности изучаемого материала. Учащиеся овладевают приемами аналитико-синтетической деятельности при доказательстве теорем и решении задач. Прикладная направленность курса обеспечивается постоянным обращением к наглядности, использованием рисунков и чертежей на всех этапах обучения и развитием геометрической интуиции на этой основе. Целенаправленное обращение к примерам из практики развивает умения учащихся вычленять геометрические факты, формы и отношения в предметах и явлениях действительности, использовать язык геометрии для их описания.

Практическая направленность курса определяется систематическим развитием геометрического аппарата для решения задач на вычисление геометрических значений

Курс алгебры построен в соответствии с традиционными содержательно-методическими линиями: числовой, функциональной, алгоритмической, уравнений и неравенств, алгебраических преобразований. В курсе алгебры продолжается систематизация сведений о преобразовании выражений и решении уравнений с одним неизвестным. Специальное внимание уделяется новым вопросам: употреблению знаков или , записи и чтению двойных неравенств, понятиям тождества, тождественного преобразования, линейного уравнения с одним неизвестным, равносильных уравнений. Формируется понятие функции, что является начальным этапом в обеспечении систематической функциональной подготовки учащихся. Продолжается изучение степени с натуральным показателем. Изучаются свойства функций и , и особенности расположения их графиков в координатной плоскости. Главное место занимают алгоритмы действий с многочленами – сложение, вычитание и умножение. Особое внимание уделяется разложению многочленов на множители с помощью вынесения за скобки общего множителя и с помощью группировки. Вырабатываются умения применять формулы сокращенного умножения как для преобразования произведения в многочлен, так и для разложения на множители. Серьезное внимание уделяется формированию умений рассуждать, делать простые доказательства, давать обоснования выполняемых действий. Параллельно закладываются основы для изучения систематических курсов стереометрии, физики, химии и других смежных предметов.

Для более широкого знакомства с математикой введен курс «Элементы статистики и теории вероятностей» в количестве 5 часов. На этом этапе продолжается решение задач путем перебора возможных вариантов, изучается статистический подход к понятию вероятности. Дается классическое определение вероятности, формируются умения вычислять вероятности с помощью формул комбинаторики. Особое внимание уделяется правилу сложения вероятностей.

Данное планирование определяет достаточный объем учебного времени для повышения математических знаний учащихся в среднем звене школы, улучшения усвоения других учебных предметов.

МЕСТО УЧЕБНОГО ПРЕДМЕТА В УЧЕБНОМ ПЛАНЕ

ЦЕЛЬ ПРОГРАММЫ	Целью обучения алгебре является формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики, как языка для построения математических моделей процессов, явлений окружающего мира. Целью обучения геометрии является развитие у учащихся пространственного воображения и логического мышления путем систематического изучения свойств геометрических фигур на плоскости и в пространстве и применения этих свойств при решении задач вычислительного и конструктивного характера
ЗАДАЧИ ПРО­ГРАММЫ	Учебные: систематизировать и обобщить сведения о числовых выражениях, об обыкновенных и десятичных дробях, полученные учащимися в курсе математики V-VI классов; научить учащихся пользоваться эквивалентными представлениями чисел в ходе решения задач, обеспечить на этой основе дальнейшее развитие вычислительных навыков и умений решать задачи на проценты, сформировать первоначальные умения статистического анализа; систематизировать и обобщить понятия пропорции и отношения, сформировать представление о прямой и обратной пропорциональных величин; научить учащихся использовать пропорции при решении задач; сформировать у учащихся первоначальные представления о языке алгебры, о буквенном исчислении; научить выполнять простейшие преобразования буквенных выражений; познакомить учащихся с понятиями уравнения и корня уравнения, с некоторыми свойствами уравнений; начать обучение решению текстовых задач алгебраическим способом, сформировать умение решать несложные линейные уравнения; развить умение, связанные с работой на координатной плоскости, познакомить с графиками зависимостей y = x, y = - x, y = x 2 , y = x 3 , y = |x|,сформировать первоначальные навыки интерпретации графиков реальных зависимостей; выработать умение выполнять действия над степенями с натуральными показателями; научить применять правило умножения при решении комбинаторных задач; выработать умение выполнять действия с многочленами, применять формулы (а + b)2 = а2 + 2 ab + b2 , (а – b)2 = а2 – 2 аb + b2.для преобразования квадрата двучлена в многочлен; выработать умение выполнять разложение многочлена на множители с помощью вынесения общего множителя за скобки и способом группировки, а также с применением формул сокращенного умножения. Развивающие: интеллектуально развивать, формировать качества личности, необходи­мые человеку для полноценной жизни в современном обществе, свойст­венных математической деятельности: ясности и точности мысли, кри­тичности мышления, интуиции, логического мышления, элементов алго­ритмической культуры, пространственных представлений, способности к преодолению трудностей; формирование представлений об идеях и методах математики как универ­сального языка науки и техники, средства моделирования явлений и про­цессов; развивать вычислительные и алгебраические знания и умения, необходимые в практической деятельности, для изучения смежных дисциплин; развивать навыки устных вычислений с множествами чисел; формировать навыки работы с уравнениями и элементарными функциями; включать обучающихся в исследовательско – поисковую деятельность как фактор личностного развития; развивать ключевых компетентностей с помощью разных методов и приемов. показать возможность оценивания вероятности случайного события по его частоте; расширить сведения о геометрических фигурах; систематизировать знания учащихся об основных свойствах простейших геометрических фигур, равенстве фигур (отрезков и углов) и свойствах измерения отрезков и углов; сформировать умение выделять равенство трех соответствующих элементов данных треугольников и делать ссылки на изученные признаки; заложить основы для изучения систематических курсов стереометрии, физики, химии и других смежных предметов; сформировать умение доказывать равенство данных треугольников, опираясь на изучен­ные признаки; отработать навыки решения простейших задач на построение с помощью циркуля и линейки; дать систематические сведения о параллельных прямых; ввести аксиому параллельных прямых; развить логическое мышление и речь – умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргу­ментации и доказательства; развитие у обучающихся внимания, способность сосредото­читься, настой­чивость, точную экономную и информативную речь, умение отби­рать наиболее подходящие языковые (сим­волические, графические) сред­ства; формирование навыков умственного труда, планирование своей деятельно­сти, поиск рациональных путей ее выполне­ния, умение крити­чески оценивать свою деятельность; развивать математическую речь, внимание; память, навыки само- и взаимопроверки; развивать сенсорную сферу и двигательную моторику. Воспитывающие: воспитывать культуру личности, отношение к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса; воспитывать волевые качества, коммуникабельность, ответственность; воспитывать уме­ние слушать, уверенность в себе и в своих знаниях, ответственность за результаты своего труда и труда товарища; воспитывать волю и настойчивость, упорство в достижении цели.
ОПИСАНИЕ МЕСТА УЧЕБНОГО ПРЕДМЕТА В ПРЕДМЕТНОМ ПЛАНЕ ШКОЫ-ИНТЕРНАТА	Предмет «Алгебра» и «Геометрия» входят в предметную область «Математика и информатика». Федеральный государственный образовательный стандарт основного общего образования предусматривает изучении предметов «Алгебра» и «Геометрия» в перечне обязательных предметов – инвариантная часть учебного плана. Федеральный базисный (общеобразовательный) учебный план предусматривает изучение алгебры в I четверти – 6 часов в неделю, во II, III, IV четвертях – 4 часа в неделю (в год 158 часов), и геометрии – во II, III, IV четвертях в объеме 2 часов в неделю в год 52 часа. Всего за год 210 часов В соответствии с расписанием, учебным планом-графиком ГКОУ РО Азовской школы-интерната №10 на 2015-2016 учебный год, утвержденным приказом от 15.06.2015г. №185 на изучение алгебры в 9-б классе отводится на изучение алгебры в I четверти – 6 часов в неделю, во II, III, IV четвертях – 4 часа в неделю (в год 158 часов), и геометрии – во II, III, IV четвертях в объеме 2 часов в неделю в год 52 часа. Всего за год 210 часов . Рабочая программа составлена: по алгебре -156 часов, по геометрии 52 час с учетом праздничных дней . Всего за год 208 часов
СТРУКТУРА УЧЕБНОГО ПРЕДМЕТА И ОСОБЕННОСТИ ПОСТРОЕНИЯ ЕЕ СОДЕРЖАНИЯ	Авторское планирование по геометрии рассчитано на 50 часов. В рабочей программе добавлено по 1 часу, которые расходуются на отработку знаний, умений и навыков по изучаемым темам: «Соотношения между сторонами и углами треугольников», «Повторение за курс геометрии в 7 классе». Авторское планирование по алгебре рассчитано на 119 часов. В рабочей программе добавлено 11 часа, которые расходуются на отработку знаний, умений и навыков по теме «Повторение за курс математики в 6 классе» и 20 часов на итоговое повторение в конце года , 3 часа добавлено на тему «Дроби и проценты», 1 час на тему «Прямая и обратная пропорциональности» , 2 часа на тему «Свойства степени с натуральным показателем» и 2 часа на тему «Разложение многочленов на множители»
УЧЕБНО-МЕТОДИЧЕСКОЕ И МАТЕРИАЛЬНО-ТЕХНИЧЕСКОЕ ОБЕСПЕЧЕНИЕ	Учебно-методические пособия: Учебник “Математика. Арифметика. Алгебра. Анализ данных” 7 класс. :Учебник для общеобразовательных учебных заведений/Г.В.Дорофеев, С.Б. Суворова, Е.А. Бунимович , Л.В. Кузнецова, С.С. Минаева ; под редакцией Г.В. Дорофеева – 3-е издание. – М.: Дрофа, 1999. – 288 с.: ил. Дидактические материалы: “ Математика 7 класс” к уч. под ред. Г.В. Дорофеева “Математика. Арифметика. Алгебра . Анализ данных” - 3 –е изд. , стереотипное- М.: Дрофа, 2000.- 176 с.: ил. Дорофеев Г.В. Алгебра: 7 кл: кн. для учителя/ Г.В. Дорофеев, С.С. Минаева, С.Б. Суворова – М.: Просвещение , 2008. Кузнецова Л.В. Алгебра: Контрольные работы для 7 – 9 классов./ Л.В. Кузнецова , С.С. Минаева, Л.О. Рослова – М . : Просвещение- 2008 . Алгебра: сборник. заданий для подготовки к итоговой аттестации в 9 классе./ Л.В. Кузнецова, С.Б. Суворова, Е.А. Бунимович и др. – М. : Просвещение , 2006 – 2008. Геометрия: 7—9 классы: учебник для общеобразовательных учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.В. Кадомцев и др. — М.: Просвещение, 2009. Изучение геометрии в 7, 8, 9 классах: методические рекомендации: Кн. для учителя / Л.С. Атанасян, В.Ф. Бутузов, Ю.А. Глазков и др. -М.: Просвещение, 2010. Гаврилова Н.Ф. Поурочные разработки по геометрии. 7 класс. М.: ВАКО, 2004 – (В помощь школьному учителю) Геометрия: дидакт. материалы для 7 кл. / Б. Г. Зив, В. М. Мейлер. — М.: Просвещение, 2004—2009. Гусев В. А. Геометрия: дидакт. материалы для 7 кл. / В.А. Гусев, А.И. Медяник. — М.: Просвещение, 2008. Самостоятельные и контрольные работы по алгебре и геометрии для 7 класса./ Ершова А. П., Голобородько В. В., Ершова А. С.— М.: Илекса, 2009 Контрольные работы по геометрии, 7 класс: к учебнику  Л. С. Атанасяна Геометрия. Тесты. 7-9 классы: учеб.-мет. пособие / П. И. Алтынов-М.: Дрофа,2005. Мищенко Т.М.. Геометрия. Тематические тесты. 7 класс/ Т.М. Мищенко, А.Д. Блинков. М.: Просвещение, 2011. «Геометрия, 7-9»/ Н. Б. Мельникова-М.: Изд. «Экзамен», 2009. Источники информации для учителя за курс алгебры Алгебра. Самостоятельные разноуровневые работы. 7 класс/ сост. Т.Л. Афанасьева, Л.А. Тапилина –Волгоград: Учитель, 2008 Арутюнян Е.Б. Математические диктанты для 5-9 классов –М.: Просвещение, 1991 Гельфман Э.Г. и др. Знакомимся с алгеброй: Учебное пособие по математике для 7 класса.-Томск,1994 Геометрия . 7 класс: Поурочные планы (по учебнику Л.С. Атанасяна и др.) –Волгоград: Учитель, 2003.-111с. Геометрия. 7-9 класы. Самостоятельные и контрольные работы к учебнику Л.С. Атанасяна: разрезные карточки/ сост. М. А. Иченская.- Волгоград: Учитель, 2007.-150с. Государственный стандарт основного общего образования по математике. Дидактические материалы по алгебре для 7 класса – 5-е изд., перераб. Гусев В.А., Медяник А.И. – М.: Просвещение, 2000-2003. Дидактические материалы по геометрии. 7 класс. / Б.Г. Зив, В.М. Мейлер. / М: Просвещение, 1999. - 126 с. Дудницын Ю.П. Алгебра.7 кл. Контрольные работы: Учебное пособие для общеобразоват.учреждений/ -М.: Мнемозина, 2006 Ершова А.П., ГолобородькоВ.В., Самостоятельные и контрольные работы по алгебре для7 класса.-М.:Илекса,-2007 Задачи повышенной трудности в курсе алгебры 7-9 классов: Книга для учителя. Н.П. Кострикина. – М.: Просвещение, 1991. Звавич Л.И. Дидактические материалы по алгебре для 7 класса – М.: Просвещение, 2002 Изучение геометрии в 7 – 9 классах. / Л.С. Атанасян, В.Ф. Бутузов, Ю.А. Глазков, В.Б. Некрасов, И.И. Юдина. Методические рекомендации к учебнику. / 3-е издание. М.: Просвещение, 2000. – 255 с. История математики в школе. VII-VIII кл. Пособие для учителей. / Г.И. Глейзер – М.: Просвещение, 1982 – 240 с. Коваленко В.Г. Дидактические игры на уроках математики –М.: Просвещение, 1990 Короткова, Л.М. Алгебра.7 класс: Тесты. Дидактические материалы/ -М.:Айриспресс,2006 Кудрявцев С.В. Дидактические материалы по алгебре для 7 класса: Пособие для учителя/ М.: Просвещение.1986 Кукарцева Г.И. Сборник задач по геометрии в рисунках и тестах. 7-9 классы./ Учебное пособие.- К.: ГИППВ, 1998, 128с. Математика. 5-11 классы: проблемно-развивающие задания, конспекты уроков, проекты/ авт.-сост. Г.Б.Полтавская,-Волгоград: Учитель , 2010 Миндюк М.Б., Миндюк Н.Г. «Разноуровневые дидактические материалы по алгебре. 7 класс» М., Издательство «Фирмы Глянц», 1995г. Мищенко Т.М., Семенов А.В. Разноуровневые дидактические карточки-задания по геометрии. 7 класс.-М.: Издательский Дом «Генжер», 1999.-48с. Мищенко Т.М., Тематические тесты по геометрии: 7 кл. к учебнику Л.С. Атанасяна и др. «Геометрия.7-9 классы»:.-М.: Издательство «экзамен», 2007.-63с. Нестандартные уроки геометрии 7-8 классы./Сост. Г.И..Григорьева.-Волгоград: ИТД «Корифей».-96 с. Никольская И.Л., Семенов Е.Е. Учимся рассуждать и доказывать: Кн. Для учащихся 6-10 кл. сред.шк.- М.: Просвещение, 1989.-192 с. Планирование обязательных результатов обучения математике/Л.о. Денищева, Л.В.Кузнецова -М.: Просвещение, 1989 Проверочные задания по математике для учащихся 5-8 и 10 классов средней школы: Пособие для учителя/ Л.М. Буланова- М.:Просвещение,1992 Программы. Математика 7-9классы / авт.-сост.. Бурмистрова Т.А. – М.: Просвещение, 2009 Пронин П.Н. Алгебра. Тетрадь с печатной основой. 7 класс Саратов: Лицей, 1998 Рабинович Е.М. Задачи и упражнения на готовых чертежах. 7-9 классы. Геометрия.-М.: Илекса. Харьков. Гимназия, 2001.-56с. Саврасова С.М., Ястребинецкий Г.А. Упражнения по планиметрии на готовых чертежах: Пособие для учителя.-М.: Просвещение, 1987.-112с. Семенов Е.Е. Изучаем геометрию: Кн.для учащихся 6-8 кл.сред. шк.-М.: Просвещение, 1987.-256с. Тесты. Геометрия 7 – 9. / П.И. Алтынов. Учебно-методическое пособие. / М.: Дрофа, 1997. – 107 с. Уроки геометрии в 7-9 классах. Методические рекомендации и примерное планирование: К учебнику Л.С. Атанасяна и др./ В.И. Жохов, Г.Д.Карташева, Л.Б.Крайнева.–Мнемозина, 2002.-247с. Фаддеев Д.К. Задачи по алгебре для 6-8 классов/ М.: Просвещение, 1988 Учебно-методический комплект ученика: Дидактические материалы по алгебре для 7 класса – 5-е изд., перераб. Гусев В.А., Медяник А.И. – М.: Просвещение, 2000-2003. История математики в школе. VII-VIII кл. Пособие для учителей. / Г.И. Глейзер – М.: Просвещение, 1982 – 240 с. Короткова, Л.М. Алгебра.7 класс: Тесты. Дидактические материалы/ -М.:Айриспресс,2006 Геометрия: 7—9 классы: учебник для общеобразовательных учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.В. Кадомцев и д. — М.: Просвещение, 2009. Геометрия, рабочая тетрадь,7 класс/ Л.С. Атанасян,   В.Ф. Бутузов и др. — М.: Просвещение, 2005-2009. Дополнительная литература: Нестандартные уроки геометрии 7-8 классы./Сост. Г.И..Григорьева.-Волгоград: ИТД «Корифей».-96 с. Семенов Е.Е. Изучаем геометрию: Кн.для учащихся 6-8 кл.сред. шк.-М.: Просвещение, 1987.-256с. Никольская И.Л., Семенов Е.Е. Учимся рассуждать и доказывать: Кн. Для учащихся 6-10 кл. сред.шк.- М.: Просвещение, 1989.-192 с. Дидактические материалы по геометрии. 7 класс. / Б.Г. Зив, В.М. Мейлер. / М: Просвещение, 1999. - 126 с. Тесты. Геометрия 7 – 9. / П.И. Алтынов. Учебно-методическое пособие. / М.: Дрофа, 1997. – 107 с. Саврасова С.М., Ястребинецкий Г.А. Упражнения по планиметрии на готовых чертежах: Пособие для учителя.-М.: Просвещение, 1987.-112с. Рабинович Е.М. Задачи и упражнения на готовых чертежах. 7-9 классы. Геометрия.-М.: Илекса. Харьков. Гимназия, 2001.-56с. Кукарцева Г.И. Сборник задач по геометрии в рисунках и тестах. 7-9 классы./ Учебное пособие.- К.: ГИППВ, 1998, 128с. Геометрия. 7-9 класы. Самостоятельные и контрольные работы к учебнику Л.С. Атанасяна: разрезные карточки/ сост. М. А. Иченская.- Волгоград: Учитель, 2007.-150с. Мищенко Т.М., Семенов А.В. Разноуровневые дидактические карточки-задания по геометрии. 7 класс.-М.: Издательский Дом «Генжер», 1999.-48с. Мищенко Т.М., Тематические тесты по геометрии: 7 кл. к учебнику Л.С. Атанасяна и др. «Геометрия.7-9 классы»:.-М.: Издательство «экзамен», 2007.-63с. Печатные пособия: Демонстрационный материал в соответствии с основными темами программы обучения Карточки с заданиями по математике Портреты выдающихся деятелей математики Учебно-практическое и учебно-лабораторное оборудование: Комплект чертежных инструментов: линейка, транспортир, угольник, циркуль. Комплекты планиметрических и стереометрических тел. Технические средства обучения: Компьютер Мультимедийный проектор Экран Информационно – методическая и Интернет поддержка: Журнал «Математика в школе» Приложение «Математика», сайт www.prov.ru (рубрика «Математика»). Интернет-школа сайт www.Просвещение.ru. Сайт www.talant Perm ru. Интернет-сайты для математиков   http://4-8class-math-forum.ru - Детский Математический Форум для школьников 4 - 8 классов. http://allbest.ru/mat.htm - Электронные бесплатные библиотеки http://catalog.alledu.ru/ - Все образование. Каталог ссылок http://center.fio.ru/som/subject.asp?id=10000191 http://comp-science.narod.ru - дидактические материалы по информатике и математике: материалы олимпиад школьников по программированию, подготовка к олимпиадам по программированию, дидактические материалы по алгебре и геометрии (6-9 кл.) в формате LaTeX и др. http://comp-science.narod.ru/ http://eidos.ru/ - Дистанционное образование: курсы, олимпиады, конкурсы, проекты, интернет-журнал "Эйдос". http://en.edu.ru/db/sect/3217/3284 - Естественно-научный образовательный портал (учебники, тесты, олимпиады, контрольные) http://kvant.mccme.ru/ - сайт Научно-популярного физико-математического журнала "Квант". http://matematika.agava.ru/ http://mathem.by.ru/index.html - Математика online http://methmath.chat.ru/index.html http://refportal.ru/mathemaics/ Рефераты по математике http://schools.techno.ru/tech/index.html http://schools.techno.ru/tech/index.html http://som.fio.ru/ - В помощь учителю. Федерация интернет-образования http://teacher.fio.ru/ - Учитель.ру – Федерация интернет-образования http://umnojenie.narod.ru/ - Способ умножения "треугольником". http://vip.km.ru/vschool/demo/education.asp?subj=292 http://www.catalog.alledu.ru/predmet/math/more2.html http://www.center.fio.ru/som - методические рекомендации учителю-предметнику (представлены все школьные предметы). Материалы для самостоятельной разработки профильных проб и активизации процесса обучения в старшей школе. http://www.edu.ru - Центральный образовательный портал, содержит нормативные документы Министерства, стандарты, информацию о проведение эксперимента. http://www.history.ru/freemath.htm - бесплатные обучающие программы по математике для школьников. http://www.internet-scool.ru  - сайт Интернет – школы издательства Просвещение. Учебный план разработан на основе федерального базисного учебного плана для общеобразовательных учреждений РФ и представляет область знаний «Математика». На сайте представлены Интернет-уроки по алгебре и началам анализа и геометрии, с включают подготовку сдачи ЕГЭ .  http://www.matematika-na.ru - Решение математических задач 5-6 классы. http://www.mathnet.spb.ru/ http://www.mathprog.narod.ru - материалы по математике и информатике для учителей и учащихся средних школ, подготовленный учителем средней общеобразовательной школы Тишиным Владимиром. http://www.otbet.ru/ Делаем уроки вместе! http://www.prosv.ru -  сайт издательства «Просвещение» (рубрика «Математика») http://www.rubricon.ru/; http://www.encyclopedia.ru/ ИНТЕРНЕТ – РЕСУРСЫ http://www.samara.fio.ru/resourse/teachelp.shtml#mate  http://www.school.edu.ru/catalog.asp?cat_ob_no=1165 - Российский образовательный портал. Каталог справочно-информационных источников http://www.school.mos.ru - сайт поможет школьнику найти необходимую информацию для подготовки к урокам, материал для рефератов и т.д. http://www.uic.ssu.samara.ru/~nauka - сайт "Путеводитель В МИРЕ НАУКИ для школьников". http://zaba.ru - сайт "Математические олимпиады и олимпиадные задачи". http:/www.drofa.ru  -  сайт издательства Дрофа (рубрика «Математика») http:/www.mnemozina.ru  - сайт издательства Мнемозина (рубрика «Математика») www.1september.ru www.allmath.ru www.math.ru www.uztest.ru Мегаэнциклопедия Кирилла и Мефодия: http://mega.km.ru Министерство образования РФ: http://www.informika.ru/; http://www.ed.gov.ru/; http://www.edu.ru/ Новые технологии в образовании: http://edu.secna.ru/main/ Педагогическая мастерская, уроки в Интернет и многое другое: http://teacher.fio.ru Путеводитель «В мире науки» для школьников: http://www.uic.ssu.samara.ru/~nauka/ Тестирование online: 5 - 11 классы:

Характеристика 9-б класса

На начало учебного года в классе 6 обучающихся: Бацунов Михаил (двусторонняя сенсоневральная тугоухость 3 степени),Гуйвенко Александдра (двусторонняя сенсоневральная тугоухость 4 степени, лёгкая умственная отсталость), Коноплин Александр (двусторонняя тугоухость 3 степени, органическое поражение центральной нервной системы), Кравченко Александр (двусторонняя тугоухость 3 степени, астеноневрологический синдром, церебрастения на смешанном резидуально-органическом фоне, лёгкая умственная отсталость), Левченко Николай (тугоухость 1-2 степени, бронхиальная астма), Страхов Никита (двусторонняя сенсоневральная тугоухость 3 степени).

Дети разновозрастные, с разными диагнозами. На уроках активны, большинство стремятся получить новые знания, осознавая важность учёбы в дальнейшей жизни. Внимание детей на уроке устойчивое.Тип внимания смешанный. В классе 4 ученика (Страхов Н., Бацунов М., Кравченко С.,.) способны анализировать, обобщать, делать самостоятельные выводы. Они отличются сообразительностью. Слабоуспевающие :Гуйвенко А., Коноплин А.,Калашник Т., Левченко Н.Эти обучающиеся трудно усваивают учебный материал, постоянно требуют контроля со стороны учителя. Эти дети отличаются быстрой утомляемостью, слабой выносливостью в умственном напряжении, лёгкой отвлекаемостью, низкой работоспособностью. С ними проводится индивидуальная работа, для повышения уровня результативности.

Промежуточная аттестация проводится в форме тестов, самостоятельных, проверочных работ и математических диктантов (по 10 - 15 минут) в конце логически законченных блоков учебного материала. Итоговая аттестация предусмотрена в виде административной контрольной работы.

Для развития устойчивого интереса к учебному процессу, уроки математики интегрируются с уроками информатики. Некоторые разделы алгебры закрепляются посредством тестов на ПК, которые разработали сами учащиеся. Для этого используется пакет прикладных программ Microsoft Office и УМК Живая математика – это компьютерная система моделирования, исследования и анализа широкого круга задач математики. Программа Живая Математика помогает конструировать интерактивные математические модели, давая начальные представления о понятиях формы тела, числах и т.п. Живая Математика помогает поставить мысленный эксперимент вида "что если?".

С учетом возрастных особенностей классов выстроена система учебных занятий (уроков), спроектированы цели, задачи, ожидаемые результаты обучения (планируемые результаты). Требования к результатам обучения конкретизированы, даны в деятельной формулировке и в последовательности их изложения. Конкретно сформулированные требования позволяют спланировать виды учебной деятельности, что обеспечит усвоение учебного материала на уровне требований Государственного стандарта. В планировании приведены примерные измерители достижения требований к уровню подготовки. Планируется использование новых педагогических технологий в преподавании предмета.

Приведение курса в соответствие с возрастными особенностями учащихся выражается в живом языке изложения и в опоре на жизненный опыт учащихся, органи­зации раз­нообразной практи­ческой деятельности.

В данном классе ведущими методами обучения предмету являются: объяснительно-иллюстративный и репродуктивный, хотя используется и частично-поисковый. На уроках используются элементы следующих технологий: личностно ориентированное обучение, обучение с применением опорных схем, проблемное обучение.

При организации учебного процесса будет обеспечена последовательность изучения учебного материала: новые знания опираются на недавно пройденный материал; обеспечено поэтапное раскрытие тем с последующей реализацией; закрепление в процессе практикумов, тренингов.

В ходе преподавания математики в 9-Б классе, работы над формированием у учащихся перечисленных в программе знаний и умений следует обращать внимание на то, чтобы они овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:

• планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;

• решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;

• исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;

• ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;

• проведения доказательных рассуждений, аргументации, вы движения гипотез и их обоснования;

• поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.

СОДЕРЖАНИЕ ПРОГРАММЫ

АЛГЕБРА

1.Повторение изученного 11ч.

2. Дроби и проценты (19 ч)

Обыкновенные и десятичные дроби, вычисления с рациональными числами. Степень с натуральным показателем. Решение задач на проценты. Статистические характеристики: среднее арифметическое, мода, размах.

Основная цель – систематизировать и обобщить сведения об обыкновенных и десятичных дробях, обеспечить на этой основе дальнейшее развитие вычислительных навыков, умение решать задачи на проценты; сформировать первоначальные умения статистического анализа числовых данных.

В соответствии с идеологией курса данная тема представляет собой блок арифметических вопросов. Основное внимание уделяется дальнейшему развитию вычислительной культуры: отрабатываются умения находить десятичные эквиваленты или десятичные приближения обыкновенных дробей, выполнять действия с числами, в том числе с использованием калькулятора. Продолжается начатая в 6 классе работа по вычислению числовых значений буквенных выражений. Вычислительные навыки учащихся получают дальнейшее развитие при изучении степени с натуральным показателем; учащиеся должны научиться находить значения выражений, содержащих действия возведения в степень, а также записывать большие и малые числа с использованием степеней числа 10. Продолжается решение задач на проценты. Однако в этой теме рассматриваются более сложные по сравнению с предыдущим годом задачи.

Основное содержание последнего блока темы – знакомство с некоторыми статистическими характеристиками. Учащиеся должны научиться в несложных случаях находить среднее арифметическое, моду и размах числового ряда.

3. Прямая и обратная пропорциональности (11ч)

Представление зависимости между величинами с помощью формул. Прямо пропорциональная и обратно пропорциональная зависимости. Пропорции, решение задачи с помощью пропорций.

Основная цель – сформировать представления о прямой и обратной пропорциональностях величин; ввести понятие пропорции и научить учащихся использовать пропорции при решении задач.

Изучение темя начинается с обобщения и систематизации знаний учащихся о формулах, описывающих зависимости между величинами. Вводится понятие переменной, которое с этого момента должно активно использоваться в речи учащихся. В результате изучения материала учащиеся должны уметь осуществлять перевод задач на язык формул, выполнять числовые подстановки в формулы, выражать переменные из формул. Особое внимание уделяется формированию представлений о прямой и обратной пропорциональной зависимостях и формулам, выражающим такие зависимости между величинами. Формируется представление о пропорции и решении задач с помощью пропорций.

4. Введение в алгебру (11 ч)

Буквенные выражения, числовые подстановки в буквенное выражение. Преобразование буквенных выражений: раскрытие скобок, приведение подобных слагаемых.

Основная цель – сформировать у учащихся первоначальные представления о языке алгебры, о буквенном исчислении; научить выполнять элементарные базовые преобразования буквенных выражений.

В 7 классе начинается систематическое изучение алгебраического материала и данная тема представляет собой первый проход соответствующего блока вопросов.

Введение буквенных равенств мотивируется опытом работы с числами, осознанием и обобщением приемов вычислений. На этом этапе раскрывается смысл свойств арифметический действий как законов преобразований буквенных выражений, формируются умения упрощать несложные произведения, раскрывать скобки, приводить подобные слагаемые.

5. Уравнения (15ч)

Уравнения. Корни уравнения. Линейное уравнение. Решение текстовых задач методом составления уравнения.

Основная цель – познакомить учащихся с понятиями уравнения и корня уравнения, с некоторыми свойствами уравнения; сформировать умения решать несложные линейные уравнения с одной переменной; начать обучение решению текстовых задач   алгебраическим способом.

Целесообразно, чтобы уравнение в курсе появилось как способ перевода фабульных ситуаций на математический язык. Такому переводу должно быть уделено достаточное внимание. Следует рассмотреть некоторые приемы составления уравнения по условию задачи, возможность составления разных уравнений по одному и тому же условию, сформировать умение выбирать наиболее предпочтительный для конкретной задачи вариант уравнения. Переход к алгебраическому методу решения задач одновременно служит мотивом для обучения способу решения уравнений. Основное внимание в этой теме уделяется решению линейных уравнений с одной переменной, показываются некоторые технические приемы решения.

6. Координаты и графики (12ч)

Числовые промежутки. Расстояние между точками на координатной прямой. Множества точек на координатной плоскости. Графики зависимостей у = х, у = х², у = х³, у =|x|. Графики реальных зависимостей.

Основная цель – развить умения, связанные с работой на координатной прямой и на координатной плоскости; познакомить с графиками зависимостей у = х, у = - х, у = х², у = х^3, у =|x|; сформировать первоначальные навыки интерпретации графиков реальных зависимостей.

При изучении курса математики в 5-6 классах учащиеся познакомились с идеей координат. В этой теме делается следующий шаг: рассматриваются различные множества точек на координатной прямой и на координатной плоскости, при этом формируется умение переходить от алгебраического описания множества точек к геометрическому изображению и наоборот. Рассматривается формула расстояния между точками координатной прямой.

При изучения темы учащиеся знакомятся с графиками таких зависимостей, как у = х, у = - х, у = х², у = х³, у =|x|. В результате учащиеся должны уметь достаточно быстро строить каждый из перечисленных графиков, указывая его характерные точки. Сформированные умения могут стать основой для выполнения заданий на построения графиков кусочно-заданных зависимостей.

Специальное внимание в данной теме уделяется работе с графиками реальных зависимостей – температуры, движения и пр., причем акцент должен быть сделан на считывание с графика нужной информации. Важно, чтобы учащиеся получили представление об использование графиков в самых различных областях человеческой деятельности.

7. Свойства степени с натуральным показателем (12ч)

Произведение и частное степеней с натуральными показателями. Степень степени, произведения и дроби. Решение комбинаторных задач, формула перестановок.

Основная цель – выработать умение выполнять действия над степенями с натуральными показателями; научить применять правило умножения при решении комбинаторных задач.

Учащимся уже знакомо определение степени с натуральным показателем, и у них есть некоторый опыт преобразований выражений, содержащих степени, на основе определения. Основное содержание данной темы состоит в  рассмотрении свойств степени и выполнении действий со степенями. Сформированные умения могут найти применение при  выполнении заданий на сокращение дробей, числители и знаменатели которых – произведения, содержащие степени.

В этой же теме продолжается обучение решению комбинаторных задач, в частности задач, решаемых на основе комбинаторного правила умножения. Дается специальное название одному из видов комбинаций – перестановки и рассматривается формула для вычисления числа перестановок. Это первая комбинаторная формула, сообщаемая учащимся.

8. Многочлены (18 ч)

Одночлены и многочлены. Сложение, вычитание и умножение многочленов. Формулы сокращенного умножения: квадрат суммы и квадрат разности, куб суммы и куб разности.

Основная цель – выработать умения выполнять действия с многочленами, применять формулы квадрата суммы и квадрата разности, куба суммы и куба разности для преобразования квадрата и куба двучлена в многочлен.

Изучение данной темы опирается на знания, полученные при изучения темы «Введение в алгебру». Используются свойства алгебраических сумм и произведений, правила раскрытия скобок и приведения подобных слагаемых. Терминами «одночлен» и «многочлен» называются такие алгебраические выражения, с которыми учащиеся, по сути, уже имели дело.

Основное внимание в данной теме уделяется рассмотрению алгоритмов выполнения действий над многочленами – сложения, вычитания, умножения, при этом подчеркивается следующий теоретический факт: сумму, разность и произведение многочленов всегда можно представить в виде многочлена. В ходе практической деятельности учащиеся должны выполнять задания комплексного характера, предусматривающие выполнение нескольких действий. Однако следует иметь в виду, что на этом этапе основным результатом является овладение собственно алгоритмами действий над многочленами, а преобразованием целых выражений будет уделено внимание еще в 8 классе. Овладение действиями с многочленами сопровождается развитием умений решать линейные уравнения и применять алгебраический метод решения текстовых задач.

9. Разложение многочленов на множители (22 ч)

Вынесение общего множителя за скобки. Способ группировки. Формула разности квадратов, формула суммы кубов и разности кубов. Решение уравнений с помощью разложения на множители.

Основная цель – Выработать умение выполнять разложение на множители с помощью вынесения общего множителя за скобки и способом группировки, а также с применением формул сокращенного умножения.

Вопрос о разложении многочлена на множители дается в виде отдельной темы, в которую отнесено также знакомство с формулами разности квадратов, разности и суммы кубов. Рассматриваются некоторые специальные приемы преобразования многочленов, после которых становится возможным применение способа группировки: разбиение какого-то члена многочлена на два слагаемых и более, а также прием «прибавить» - «вычесть». 

Важно, чтобы формируемый аппарат нашел применение. Поэтому в ходе изучения темы целесообразно продолжить формирование умений сокращать дроби и рассмотреть приемы решения уравнений на основе равенства произведения нулю.

10. Частота и вероятность (5 ч)

Частота случайного события. Оценка вероятности случайного события по его частоте. Сложение вероятностей.

Основная цель – показать возможность оценивания вероятности случайного события по его частоте.

Особенностью предлагаемой методики является статистический подход к понятию вероятности: вероятность случайного события оценивается по его частоте при проведении достаточно большой серии экспериментов. Такой подход требует реального проведения опытов в ходе учебного процесса. Так как для стабилизации частоты необходимо большое число экспериментов, то рекомендуется такая форма урока, как работа в малых группах. Процесс стабилизации частоты полезно иллюстрировать с помощью графика.

11. Повторение (21 ч)

ГЕОМЕТРИЯ

1. Начальные геометрические сведения (7 часов.)

Простейшие геометрические фигуры: прямая, точка, отрезок, луч, угол. Понятие равенства геометрических фигур. Сравнение отрезков и углов. Измерение отрезков, длина отрезка. Измерение углов, градусная мера угла. Смежные и вертикальные углы, их свойства. Перпендикулярные прямые.

Основная цель — систематизировать знания учащихся о простейших геометрических фигурах и их свойствах; ввести понятие равенства фигур.

В данной теме вводятся основные геометрические понятия и свойства простейших геометрических фигур на основе наглядных представлений учащихся путем обобщения очевидных или известных из курса математики 1—6 классов геометрических фактов. Понятие аксиомы на начальном этапе обучения не вводится, и сами аксиомы не формулируются в явном виде. Необходимые исходные положения, на основе которых изучаются свойства геометрических фигур, приводятся в описательной форме. Принципиальным моментом данной темы является введение понятия равенства геометрических фигур на основе наглядного понятия наложения. Определенное внимание должно уделяться практическим приложениям геометрических понятий.

2. Треугольники (14 часов)

Треугольник. Признаки равенства треугольников. Перпендикуляр к прямой. Медианы, биссектрисы и высоты треугольника. Равнобедренный треугольник и его свойства. Задачи на построение с помощью циркуля и линейки.

Основная цель — ввести понятие теоремы; выработать умение доказывать равенство треугольников с помощью изученных признаков; ввести новый класс задач — на построение с по мощью циркуля и линейки.

Признаки равенства треугольников являются основным рабочим аппаратом всего курса геометрии. Доказательство большей части теорем курса и также решение многих задач проводится по следующей схеме: поиск равных треугольников — обоснование их равенства с помощью какого-то признака — следствия, вытекающие из равенства треугольников. Применение признаков равенства треугольников при решении задач дает возможность постепенно накапливать опыт проведения доказательных рассуждений. На начальном этапе изучения и применения признаков равенства треугольников целесообразно использовать задачи с готовыми чертежами.

3. Параллельные прямые (9 часов)

Признаки параллельности прямых. Аксиома параллельных прямых. Свойства параллельных прямых.

Основная цель — ввести одно из важнейших понятий — понятие параллельных прямых; дать первое представление об аксиомах и аксиоматическом методе в геометрии; ввести аксиому параллельных прямых.

Признаки и свойства параллельных прямых, связанные с углами, образованными при пересечении двух прямых секущей (накрест лежащими, односторонними, соответственными), широко используются в дальнейшем при изучении четырехугольников, подобных треугольников, при решении задач, а также в курсе стереометрии.

1. Соотношения между сторонами и углами треугольника (17 часов)

Сумма углов треугольника. Соотношение между сторонами и углами треугольника. Неравенство треугольника. Прямоугольные треугольники, их свойства и признаки равенства. Расстояние от точки до прямой. Расстояние между параллельными прямыми. Построение треугольника по трем элементам.

Основная цель — рассмотреть новые интересные и важные свойства треугольников.

В данной теме доказывается одна из важнейших теорем геометрии — теорема о сумме углов треугольника. Она позволяет дать классификацию треугольников по углам (остроугольный, прямоугольный, тупоугольный), а также установить некоторые свойства и признаки равенства прямоугольных треугольников.

Понятие расстояния между параллельными прямыми вводится на основе доказанной предварительно теоремы о том, что все точки каждой из двух параллельных прямых равноудалены от другой прямой. Это понятие играет важную роль, в частности используется в задачах на построение.

При решении задач на Построение в 7 классе следует ограничиться только выполнением и описанием построения искомой фигуры. В отдельных случаях можно провести устно анализ и доказательство, а элементы исследования должны присутствовать лишь тогда, когда это оговорено условием задачи.

5. Повторение. Решение задач. (5 часов)

ОСНОВНЫЕ ТЕМЫ:

По алгебре: 156 часов
1. ПОВТОРЕНИЕ…………………………………………………………………………	11 часа
2. ДРОБИ И ПРОЦЕНТЫ………………………………………………………………..	19 часов
3. ПРЯМАЯ И ОБРАТНАЯ ПРОПОРЦИОНАЛЬНОСТИ…………………………….	11 часов
4. ВВЕДЕНИЕ В АЛГЕБРУ……………………………………………………………	11 часов
5. УРАВНЕНИЯ…………………………………………………………………………	15 часов
6. КООРДИНАТЫ И ГРАФИКИ………………………………………………………	12 часов
7. СВОЙСТВА СТЕПЕНИ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ………………….	12 часов
8. МНОГОЧЛЕНЫ………………………………………………………………………..	18 часов
9. РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ…………………………….	22 часов
10. ЧАСТОТА И ВЕРОЯТНОСТЬ………………………………………………………	5 часов
11. ИТОГОВОЕ ПОВТОРЕНИЕ……………………………………………………….	20часов
По геометрии: 52 часа
1. НАЧАЛЬНЫЕ ГЕОМЕТРИЧЕСКИЕ СВЕДЕНИЯ………………………………….	7 часов
2. ТРЕУГОЛЬНИКИ………………………………………………………….…………	14 часов
3. ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ………………………………………………………..	9 часов
4.СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА……...	17 часов
5. ИТОГОВОЕ ПОВТОРЕНИЕ………………………………………………………..	5 часов

ВСЕГО 208 часов

ПЕРЕЧЕНЬ КОНТРОЛЬНЫХ РАБОТ ПО АЛГЕБРЕ

№п/п	Название контрольных работ	Дата проведения
1	Контрольная работа Диагностическая контрольная работа
2	Контрольная работа «Прямая и обратная пропорциональности»	15.10
3	Контрольная работа « Введение в алгебру»	29.10
4	Контрольная работа «Уравнения»	30.11
5	Контрольная работа «Координаты и графики»	21.12
6	Контрольная работа « Свойства степени с натуральным показателем»	25.01
7	Контрольная работа «Многочлены»	25.02
8	Контрольная работа « Разложение многочленов на множители»	11.04
9	Итоговая контрольная работа

ПЕРЕЧЕНЬ КОНТРОЛЬНЫХ РАБОТ ПО ГЕОМЕТРИИИ

№п/п	Название контрольных работ	Дата проведения
1	Контрольная работа № 1 по теме «Измерение отрезков и углов».	2.12
2	Контрольная работа № 2 по теме «Треугольники».	3.02
3	Контрольная работа № 3 по теме «Параллельные прямые».	2.03
4	Контрольная работа № 4 по теме: «Соотношение между сторонами и углами треугольника »	31.03

ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ

В результате изучения курса алгебры ученик научится::

знать:

• приемы выполнения действий с рациональными числами;

• определение степени с натуральным показателем;

• правила, с помощью которых десятичная дробь выражается в процентах, и наоборот, проценты записываются в виде десятичной дроби.

уметь:

• сравнивать дроби;

• свободно переходить от десятичных дробей к обыкновенным;

• находить десятичные эквиваленты, десятичные приближения обыкновенных дробей;

• применять калькулятор;

• пользоваться определением степени с натуральным показателем для записи выражений более компактно;

• свободно переходить от дроби к процентам и наоборот;

• решать задачи.

• часто используемые формулы;

• какие величины называются переменными;

• какие величины называются прямо (обратно) пропорциональными;

уметь:

• анализировать задание и устанавливать зависимость;

• вычислять значение одних величин по значениям других;

• определять вид зависимости;

• находить коэффициент пропорциональности;

• применять основное свойство пропорции;

• алгоритм преобразования буквенных выражений;

• алгоритм раскрытия скобок;

• алгоритм приведения подобных слагаемых;

Уметь:

• составлять формулу;

• вычислять по формулам;

• выполнять замену одного буквенного выражения другим;

• раскрывать скобки;

• выполнять подстановку;

• выполнять комплексные задания;

• упрощать выражения;

Понимать:

• термин «раскрыть скобки»;

• правило раскрытия скобок;

Знать:

• алгоритм решения уравнений

• свойство уравнений;

• общий вид линейных уравнений;

• что значит решить уравнение

Уметь:

• перевести условие задачи на алгебраический язык;

• составлять разные уравнения по одному и тому же условию;

• анализировать условие задачи;

• записывать ответ;

Понимать:

• что значит «решить уравнение»;

Знать:

• уравнения осей координат;

• формулу задания биссектрисы;

Уметь:

• свободно переходить от алгебраической записи числовых промежутков к их геометрическому изображению и наоборот;

• строить точки по их координатам, отмечать координаты отмеченных точек;

• пользоваться знаками , ;

• быстро изображать прямые у=х, у= -х;

• соотносить графики зависимостей с соответствующими формулами.

Понимать:

- графический способ – один из самых удобных и наглядных способов представления и анализа информации.

Знать:

• наизусть часто встречающиеся квадраты и кубы чисел;

• что при возведении отрицательного числа в нечетную степень получается отрицательное число;

• правило умножения;

• терминологию;

• формулу для вычисления числа перестановок;

• понятие факториал».

Уметь:

- определять порядок действий при вычислении значений выражений, содержащих степени;

- возводить в степень положительное (отрицательное) число, обыкновенную, десятичную дроби;

- возводить степень в степень;

- возводить в степень произведение и дробь;

- решать несложные задачи.

Знать:

• терминологию;

• распределительное свойство умножения;

• что произведение двух многочленов – это многочлен, число членов о равно произведению числа членов данных многочленов.

Уметь:

- находить сумму и разность многочленов;

- находить значение многочлена;

- упрощать многочлен, выражения;

- выполнять числовые подстановки;

- приводить подобные слагаемые;

- раскрывать скобки;

- умножать одночлен на многочлен;

- умножать многочлен на многочлен;

- использовать прием замены;

- использовать формулу квадрата суммы (разности);

- выделять квадрат двучлена;

- упрощать выражение;

- по условию задачи сделать рисунок или схему;

- составлять и решать уравнения.

Знать:

- приемы разложения на множители;

- что при вынесении общего множителя за скобки в оставшейся в скобках сумме должно оказаться столько слагаемых, сколько их было в исходном многочлене;

- формулы сокращенного умножения;

- что формула (a²-b²) позволяет разложить многочлен на множители;

- знать формулы разности и суммы кубов для разложения на множители;

- распознавать формулы сокращенного умножения;

- приемы разложения многочлена на множители;

Уметь:

- выполнять разложение многочлена на множители с помощью вынесения общего множителя за скобки;

- выбирать способ разложения многочлена на линейные множители;

- применять формулу a²-b²=(a-b)(a+b);

- применять формулы разности и суммы кубов для разложения на множители;

- распознавать формулы сокращенного умножения;

- выбрать рациональный прием разложения на множители;

- комментировать решение;

- решать уравнения с помощью разложения на множители, применяя различные приемы;

- выполнять преобразования.

Уметь:

- находить частоту события, используя собственные наблюдения и готовые статистические данные;

- находить вероятности случайных событий в простейших случаях.

• приводить в систему свои знания по арифметике: вычисление значений числовых выраже­ний, свойства арифметических действий, порядок выполнения действий, преобразования числовых и буквенных выражений, раскрытие скобок и заключение в скобки, вычисление алгебраической суммы;

• правильно употреблять термины «выражение», «тождественное преобразова­ние», пони­мать формулировку заданий: «упростить выражение», «разложить на множи­тели»;

• составлять несложные буквенные выражения и формулы; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления; выражать из формул одни переменные через другие;

• выполнять действия со степенями с натуральным показателем, многочленами, алгебраиче­скими дробями; выполнять разложение многочленов на множители вынесе­нием общего множителя за скобки, применением формул сокращенного умножения;

• уметь приводить одночлены и многочлены к стандартному виду;

• хорошо понимать, что уравнение – это математический аппарат решения разнообразных за­дач математики, смежных областей знаний, практики;

• правильно употреблять термины «уравнение», «система», «решение системы», «корень уравнения», понимать их в тексте, в речи учителя, понимать формулировку задачи «ре­шить уравнение»;

• уметь решать линейные уравнения и уравнения, сводящиеся к ним, проверять решение уравнений;

• усвоить способы подстановки и сложения, уметь геометрически иллюстрировать решение системы, решать текстовые задачи с помощью составления систем уравнений;

• понимать что функция – это математическая модель, позволяющая описывать и изучать раз­нообразные зависимости между реальными величинами;

• правильно употреблять функциональную терминологию (значение функции, аргумент, гра­фик функции);

• уметь строить точки на координатной плоскости по их координатам, находить координаты данной точки на плоскости, строить график линейной функции;

• интерпретировать в несложных случаях графики реальных зависимостей между величи­нами, отвечая на поставленные вопросы;

• использовать приобретенные знания, умения, навыки в практической деятельности и повседневной жизни для:

• решения несложных практических расчетных задач, в том числе с использованием при необходимости справочной литературы, калькулятора, компьютера;

• устной прикидки и оценки результата вычислений, проверки результата вычислений выполнением обратных действий;

• моделирования практических ситуаций и исследовании построенных моделей с использованием аппарата алгебры;

• 

• 

В таблице показан расход электроэнергии некоторой семьей в течение года:

Месяц	1	2	3	4	5	6	7	8	9	10	11	12
Расход электроэнергии, квтч	85	80	74	62	54	68	58	54	58	64	74	86

Найдите средний ежемесячный расход электроэнергии этой семьей.

В результате изучения курса алгебры ученик получит возможность нау­читься:

Уметь выполнять действия с обыкновенными дробями.

        Уметь выполнять действия с положительными и отрицательными числами.

        Уметь выполнять раскрытие скобок, приведение подобных слагаемых.

        Уметь решать текстовые задачи.

• Знать как используются математические формулы для решения математических и практических задач.

• Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни для выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами.

• Знать как используются уравнения для решения математических и практических задач.

• Понимать, что уравнения – это математический аппарат решения разнообразных задач из математики, смежных областей знаний, практики.

• Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни для анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц.

• Понимать различные статистические утверждения.

• 

• Задание: В организации вели ежедневный учет поступивших в течение месяца писем. В результате получили такой ряд данных: 39, 43, 40, 0, 56, 38, 24, 21, 35, 38, 0, 58, 31, 49, 38, 25, 34, 0, 52, 40, 42, 40, 39, 54, 0, 64, 44, 50, 38, 37, 32. Для полученного ряда данных найдите среднее арифметическое, размах и медиану. Каков практический смысл этих показателей?

• 

• 

-Уметь выполнять действия с обыкновенными и десятичными дробями.

        Уметь выполнять тождественные преобразования алгебраических выражений.

        Знать формулы сокращенного умножения и применять их в различных случаях.

• Понимать, что функция – это математическая модель, позволяющая описывать и изучать разнообразные зависимости между реальными величинами.

• Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни для интерпретации графиков реальных зависимостей между величинами.

• Уметь выполнять действия со степенями с натуральными показателями.

• Уметь выполнять действия с одночленами.

• Уметь выполнять основные действия с многочленами.

• Уметь выполнять разложение многочленов на множители.

• Уметь выполнять разложение многочленов на множители.

• Знать формулы сокращенного умножения.

• Знать формулы разности квадратов, формулы суммы кубов и разности кубов.

• Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни для нахождения нужной формулы в справочных материалах.

• Уметь решать системы линейных уравнений.

• Уметь решать текстовые задачи с помощью систем уравнений.

• Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни для выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами.

• Понимать, что уравнения – это математический аппарат решения разнообразных задач из математики, смежных областей знаний, практики.

• Уметь выполнять действия со степенями с натуральными показателями.

• Уметь выполнять основные действия с многочленами.

• Уметь выполнять комбинированные упражнения на действия с алгебраическими дробями.

• Понимать, что функция – это математическая модель, позволяющая описывать и изучать разнообразные зависимости между реальными величинами.

• Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни для интерпретации графиков реальных зависимостей между величинами.

• Уметь решать системы двух линейных уравнений.

• Уметь решать текстовые задачи с помощью систем уравнений.

В результате изучения курса геометрии ученик научится:

• Понимать, что геометрические формы являются идеализированными образами реальных объектов; использовать геометрический язык для описания предметов окру­жающего мира; получить представление о некоторых областях применении геометрии в быту, науке, технике, искусстве.

• Распознать на чертежах и моделях геометрические фигуры (точки, прямые, лучи, отрезки, углы, треугольники и их частные виды), различать их взаимное расположение; изображать и обозначать указанные геомет­рические фигуры; выполнять чертежи по условию задачи.

• Формулировать понятие равенства геометрических фигур и сравнивать их на основе наглядного понятия наложения.

• Формулировать определение треугольника, распознавать виды треугольников (прямоугольный, остроугольный, тупоугольный, равнобедренный и равносторонний) и изображать их на чертеже.

• Формулировать признаки равенства треугольников, доказывать равенство треугольников с помощью изученных признаков.

• Владеть практическими навыками использования геометрических инструментов для изобра­жения фигур, строить треугольники с помощью циркуля и линейки, а также для нахождения длин отрезков.

• Сравнивать отрезки и углы, находить градусные меры углов с помощью транспортира.

• Решать задачи на вычисления геометрических величин (длин отрезков, градусную меру углов), применяя изученные формулы и свойства и проводить аргументацию в ходе решения задач.

• Н ачертите три неразвернутые

угла и обозначьте каждый из них

одним из трех способов.

• Определите длину ломаной АВСD

  1. Треугольники АВС и PQR равны. Известно, что сторона АВ=10 см, а угол С равен 90^о. Чему равны сторона PQ и угол R?

  2. Постройте треугольник по трем данным сторонам а, b и с с помощью циркуля и линейки.

На рисунке точка О является серединой отрезка АС. ВАО= DCO. Докажите равенство треугольников АВО и CDO.

1. Найдите углы, образованные при пересечении биссектрис острых углов прямоугольного равнобедренного треугольника.

2. Докажите, что биссектриса угла образует с его сторонами углы не больше 90^о.

1. Периметр равнобедренного треугольника равен 1 м, а основание равно 0,4 м. Найдите длину боковой стороны.

2. В треугольнике АВС А = 50^о, В = 65^о. Через вершину В проведена прямая ВК так, что луч ВС – биссектриса угла АВК.

Докажите, что АС // ВК.

3. Построить прямоугольный треугольник по катету и прилегающему к нему острому углу.

• Формулировать понятия середины отрезка, биссектрисы угла, медианы, биссектрисы и высоты треугольника.

• Формулировать определения и свойства смежных, вертикальных углов, перпендикулярных прямых.

• Строить смежные, вертикальные углы, находить их на рисунке, решать задачи.

• Формулировать признаки и свойства параллельных прямых, связанные с углами, образованными при пересечении двух прямых секущей, применять эти свойства при решении задач.

• Формулировать теорему о сумме углов треугольника, уметь ее доказывать.

• Формулировать признаки равенства прямоугольных треугольников, строить треугольник по трем элементам, применять полученные знания при решении задач.

• Решать задачи на доказательство, уметь рассуждать, делать простые доказательства, давать обоснования выполняемым действиям.

• Формулировать определение окружности и её элементов

• Владеть алгоритмом решения задач на построение.

• Выполнять чертеж по условию планеметрической задачи.

• Понимать планеметрические чертежи.

• Использовать приобретенные знания, умения, навыки в практической деятельности и повседневной жизни для:

• описания реальных ситуаций на языке геометрии;

• решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства);

• построений геометрическими инструментами (линейка, угольник, циркуль, транспортир).

В результате изучения курса геометрии ученик получит возможность научиться:

• Уметь решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними.

--Уметь решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними. Например:

- Точки А,В и С лежат на одной прямой. Может ли точка В разделить точки А и С, если АС=7 м, ВС =7,6 м? Объясните ответ.

- Даны прямая и три точки А, В, С, не лежащие на одной прямой. Известно, что отрезок АВ пересекает прямую, а отрезок АС не пересекает ее. Пересекает ли прямую отрезок ВС? Объясните ответ.

- Треугольники АВС и PQR равны. Точка К – середина стороны АС, а точка М – середина стороны РR. Докажите, что ВК=QM.

- Постройте треугольник по данным стороне, прилежащему к ней углу и проведенной к ней высоте.

- Докажите, что две прямые либо параллельны, либо пересекаются в одной точке.

- Найдите смежные углы, если один из них в 2 раза больше другого.

- В треугольнике АВС медиана ВМ равна половине стороны АС найдите угол В треугольника.

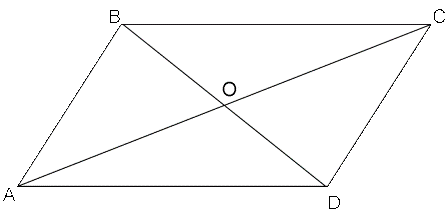- На рисунке ВО = OD и AO = OC. Докажите, что .

- Постройте треугольник по острому углу и двум высотам, проведенным к сторонам, образующим данный угол.

1. Уметь проводить доказательные рассуждения при решении задач, используя известные теоремы.

в направлении личностного развития:

• Овладение знаниями о важнейших этапах развития математики (изобретение десятичной нумерации, обыкновенных дробей, десятичных дробей, положительных и отрицательных чисел; происхождение геометрии из практических потребностей людей);

• Умение строить речевые конструкции с использованием изученной терминологии и символики (устные и письменные), понимать смысл поставленной задачи, выстраивать аргументацию, выполнять перевод с естественного языка на математический и наоборот;

• Стремление к критичности мышления, распознаванию логически некорректного высказывания, различению гипотезы и факта;

• Стремление к самоконтролю процесса и результата учебной математической деятельности;

• Способность к эмоциональному восприятию математических понятий, логических рассуждений, способов решения задач, рассматриваемых проблем.

В метапредметном направлении:

• Сформированность первоначальных представлений о математике как универсальном языке науки и техники, средстве моделирования явлений и процессов;

• умение понимать и использовать математические средства наглядности (схемы, таблицы, диаграммы, графики) для иллюстрирований содержания сюжетной задачи или интерпретации информации статистического плана;

• способность наблюдать, сопоставлять факты, выполнять аналитико-синтетическую деятельность; умение выдвигать гипотезы при решении учебно-познавательных задач, понимать необходимость их проверки, обоснования;

• умение выстраивать цепочку несложных доказательных рассуждений, опираясь на изученные понятия и их свойства;

• способность разрабатывать простейшие алгоритмы на материале выполнения действий с натуральными числами, обыкновенными и десятичными дробями, положительными и отрицательными числами;

• понимание необходимости применять приемы самоконтроля при решении задач;

• стремление продуктивно организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределять функции и роли участников, взаимодействовать и находить общие способы работы; умение работать в группе, слушать партнера . формулировать. Аргументировать и отстаивать свое мнение;

• сформулировать основы учебной и общепользовательской компетентности в области использования информационно-коммуникационных технологий (ИКТ-компетентности);

• способность видеть математическую задачу в других дисциплинах, в окружающей жизни (простейшие ситуации)

в предметном направлении:

- умение работать с математическим текстом (структурирование,извлечение необходимой информации), точно играмотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику, использовать различные языки математики(словесный, символический,графический);развитие способности обосновывать суждения, проводить классификацию;

- владение базовым понятийным аппаратом: иметь представление о числе, дроби,процентах, об основных геометрических объектах (точка, прямая, ломаная, луч, угол,многоугольник, многогранник, круг, окружность,шар,сфера, цилиндр, конус), о достоверных и случайных событиях;

-овладение практически значимыми математическими умениями и навыками, их применением к решению математических и нематематических задач, предполагающие умение:

выполнять устные, письменные, инструментальные вычисления;

выполнять алгебраические преобразования для упрощения простейших буквенных выраженний;

использоватгеометрический язык для описания предметов окружающего мира;

измерять длины отрезков, величины углов, использовать формулы для нахождения периметров, площадей, объемов геометрических фигур; пользоваться формулами площади, объема, пути для вычисления значений неизвестной величины;

решать простейшие линейные уравнения.

Оценка уровня обученности обучающихся по предмету производится в соответствии с требованиями программы. При отслеживании результатов учитываются индивидуальные особенности учеников.

Контроль над предметными компетенциями учащихся осуществляется через виды и формы контроля: промежуточный, текущий, итоговый, тематический, периодический, поурочный, индивидуальный, фронтальный..

При проверке усвоения материала необходимо выявлять полноту, прочность усвоения учащимися теории и умения применять ее на практике в знакомых и незнакомых ситуациях, формировать компетенции: ключевые образовательные компетенции, коммуникативную компетенцию, интеллектуальную компетенцию, компетенцию продуктивной творческой деятельности, информационную компетенцию, рефлексивную компетенцию.

Промежуточная аттестация учебных курсов алгебры и геометрии осуществляется через математические диктанты, самостоятельные и контрольные работы по разделам учебного материала, тесты, творческие и исследовательские задания. Итоговая аттестация предусмотрена в виде итоговой контрольной работы.

Предлагаются обучающимся разноуровневые работы, т.е. список заданий делится на две части – обязательную и необязательную. Обязательный уровень обеспечивает базовые знания для любого ученика. Необязательная часть рассчитана на более глубокие знания темы. Цель: способствовать развитию устойчивого умения и знания согласно желаниям и возможностям учащихся.

Задания для устного и письменного опроса учащихся состоят из теоретических вопросов и задач

ИЗМЕРИТЕЛИ УРОВНЯ ПОДГОТОВКИ УЧАЩИХСЯ. По алгебре:
Тема	Вопросы выносимые на контроль	Вид контроля	Продол­житель­ность работы
ПОВТОРЕНИЕ	1. Действия с дробями.	Сам. работа	10 мин.
	2. Действия с противоположными числами.	Сам. работа	10 мин.
	3. Проверка знаний, полученных в 8 классе.	Диагности-ческая работа	40 мин.
ДРОБИ И ПРОЦЕНТЫ	1. Обыкновенные и десятичные дроби.	Сам. работа	15 мин.
	2. Степень с натуральным показателем.	Мат. диктант	5 мин.
	3. Задачи на проценты.	Сам. работа	15 мин.
	4. Статистические характеристики.	Практич. работа	7 мин.
	5. Проверка знаний по теме.	Контр. работа №1	40 мин.
ОТНОШЕНИЯ И ПРОПОРЦИИ.	1. Что такое отношение.	Мат. диктант	5 мин.
	2. Деление в данном отношении.	Сам. работа	15 мин.
	3. Пропорции	Мат. диктант	5 мин.
	4. Прямая и обратная пропорциональности.	Сам. работа	15 мин.
	5. Решение задач.	Сам. работа	20 мин.
	6. Проверка знаний по теме.	Контр. работа №2	40 мин.
ВВЕДЕНИЕ В АЛГЕБРУ.	1. Буквенные выражения и числовые подстановки.	тест	10 мин.
	2. Буквенная запись свойств действий над числами.	Мат. диктант	7 мин.
	3. Преобразование буквенных выражений.	тест	15 мин.
	4. Раскрытие скобок.	тест	20 мин.
	5. Приведение подобных слагаемых.	тест	10 мин.
	6. Проверка знаний по теме.	Контр. работа №3	40 мин.
УРАВНЕНИЯ.	1. Алгебраический способ решения задач.	Сам. работа.	10 мин.
	2. Корни уравнения.	Мат. диктант	7 мин.
	3. Решение уравнений.	Сам. работа	25 мин.
	4. Решение задач с помощью уравнений.	тест	15 мин.
	5. Проверка знаний по теме.	Контр. работа №4	40 мин.
КООРДИНАТЫ И ГРАФИКИ.	1. Множества точек на координатной прямой.	Сам. работа	15 мин.
	2. Множества точек на координатной плоскости.	Сам. работа	15 мин.
	3. Графики.	Сам. работа.	15 мин.
	4. Еще несколько важных графиков.	тест	5 мин.
	5. Графики вокруг нас.	Сам. работа.	20 мин.
	6. Проверка знаний по теме.	Контр. работа №5	40 мин.
СВОЙСТВА СТЕПЕНЕЙ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ.	1. Произведение и частное степеней.	Мат. диктант	10 мин.
	2. Степень степени, произведения и дроби.	Мат. диктант	10 мин.
	3. Решение комбинаторных задач.	тест	10 мин.
	4. Перестановки.	Сам. работа	15 мин.
	5. Проверка знаний по теме.	Контр. работа №6	40 мин.
МНОГОЧЛЕНЫ	1. Одночлены и многочлены.	Мат. диктант	7 мин.
	2. Сложение и вычитание многочленов.	Сам. работа.	15 мин.
	3. Умножение многочлена на одночлен.	Сам. работа.	15 мин.
	4. Умножение многочлена на многочлен.	Сам. работа.	10 мин.
	5. Формулы квадрата суммы и квадрата разности.	Сам. работа.	20 мин.
	6. Решение задач с помощью уравнений.	Сам. работа.	20 мин.
	7. Проверка знаний по теме.	Контр. работа №7	40 мин.
РАЗЛОЖЕНИЕ МНОГОЧЛЕ-НОВ НА МНОЖИТЕЛИ	1. Вынесение общего множителя за скобки.	Сам. работа	7 мин.
	2. Способ группировки.	Сам. работа.	15 мин.
	3. Формула разности квадратов.	Мат. диктант.	5 мин.
	4. Формула разности и суммы кубов.	Мат. диктант	10 мин.
	5. Разложение на множители с применением нескольких способов.	Сам. работа.	20 мин.
	6. Решение уравнений с помощью разложения на множители.	Сам. работа.	20 мин.
	7. Проверка знаний по теме.	Контр. работа №8.	40 мин.
ЧАСТОТА И ВЕРОЯТНОСТЬ	1. Относительная частота случайного события.	Сам. Работа	15 мин.
	2. Вероятность случайного события.	Сам. работа	20 мин.
ИТОГОВОЕ ПОВТОРЕНИЕ	Повторение изученного в 9 классе.	Итоговая контр. работа.	40 мин.
По геометрии:
Тема	Вопросы выносимые на контроль	Вид контроля	Продол­житель­ность работы
НАЧАЛЬНЫЕ ГЕОМЕТРИЧЕСКИЕ СВЕДЕНИЯ.	1. Прямая и отрезок.	Сам. работа.	10 мин..
	2. Луч и угол.	Мат. диктант	5 мин.
	3. Сравнение отрезков и углов.	Сам. работа.	15 мин..
	4. Измерение отрезков.	Практ. работа.	10 мин..
	5. Измерение углов.	Практ. работа.	10 мин..
	6. Перпендикулярные прямые.	Мат. диктант.	7 мин.
	7. Решение задач.	Сам. работа.	20 мин.
	8. Проверка знаний по теме.	Контрольная работа № 1.	40 мин.
ТРЕУГОЛЬ-НИКИ.	9. Первый признак равенства треугольников.	Сам. работа.	15 мин.
	10. Медианы, биссектрисы и высоты треугольника.	Устный опрос.	5 мин.
	11. Второй и третий признаки равенства треугольников.	Сам. работа.	15 мин.
	12. Задачи на построение.	Практ. работа.	40 мин.
	13.Решение задач.	Тест	20 мин.
	14. Проверка знаний по теме.	Контрольная работа № 2.	40 мин.
ПАРАЛЛЕЛЬ-НЫЕ ПРЯМЫЕ.	15. Признаки параллельности двух прямых.	Мат. диктант	10 мин.
	16. Аксиома параллельных прямых.	Письменный опрос	15 мин.
	17. Решение задач.	Сам. работа.	20 мин.
	18. Проверка знаний по теме.	Контрольная работа № 3.	40 мин.
СООТНОШЕ-НИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИ-КА.	19. Сумма углов треугольника.	Тест	10 мин.
	20. Соотношения между сторонами и углами треугольника.	Сам. работа.	15 мин.
	21. Проверка знаний по теме.	Контрольная работа № 4.	40 мин.
	22. Прямоугольные треугольники.	Тест	15 мин.
	23. Построение треугольника по его трем элементам.	Практ. работа	10 мин.
	24.Решение задач.	Сам. работа.	30 мин.
	25. Проверка знаний по теме.	Контрольная работа № 5.	40 мин.
ИТОГОВОЕ ПОВТОРЕНИЕ.	26. Решение задач.	Итоговая контрольная работа	40 мин.

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ КРИТЕРИЕВ ОЦЕНИВАНИЯ ЗНАНИЙ, УМЕНИЙ И НАВЫКОВ ОБУЧАЮЩИХСЯ

Оценка ответа учащегося при устном и письменном опросе проводится по пятибалльной системе, т. е. за ответ выставляется одна из отметок: 1 (плохо), 2 (неудовлетвори­тельно), 3 (удовлетворительно), 4 (хорошо), 5 (отлично).

по геометрии

Оценка письменных контрольных работ.

Ответ оценивается отметкой «5», если:

• работа выполнена полностью;

• в логических рассуждениях и обосновании решения нет пробелов и ошибок;

• в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).

Отметка «4» ставится в следующих случаях:

• работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);

• допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).

Отметка «3» ставится, если:

• допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.

Отметка «2» ставится, если:

• допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.

Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.

Оценка устных ответов.

Ответ оценивается отметкой «5», если ученик:

• полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;

• изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;

• правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;

• показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;

• продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;

• отвечал самостоятельно, без наводящих вопросов учителя;

• возможны одна – две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.

Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:

• в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;

• допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;

• допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.

Отметка «3» ставится в следующих случаях:

• неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала;

• имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;

• ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;

• при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.

Отметка «2» ставится в следующих случаях:

• не раскрыто основное содержание учебного материала;

• обнаружено незнание учеником большей или наиболее важной части учебного материала;

• допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя

При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.

Грубыми считаются ошибки:

• незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;

• незнание наименований единиц измерения;

• неумение выделить в ответе главное;

• неумение применять знания, алгоритмы для решения задач;

• неумение делать выводы и обобщения;

• неумение читать и строить графики;

• неумение пользоваться первоисточниками, учебником и справочниками;

• потеря корня или сохранение постороннего корня;

• отбрасывание без объяснений одного из них;

• равнозначные им ошибки;

• вычислительные ошибки, если они не являются опиской;

• логические ошибки.

К негрубым ошибкам следует отнести:

• неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;

• неточность графика;

• нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);

• нерациональные методы работы со справочной и другой литературой;

• неумение решать задачи, выполнять задания в общем виде.

Недочетами являются:

• нерациональные приемы вычислений и преобразований;

• небрежное выполнение записей, чертежей, схем, графиков.

В основу критериев оценки учебной деятельности учащихся положены объективность и единый подход. При 5-балльной оценке для всех установлены общедидактические критерии.

Оценка "5" ставится в случае:

1. Знания, понимания, глубины усвоения обучающимся всего объёма программного материала.

2. Умения выделять главные положения в изученном материале, на основании фактов и примеров обобщать, делать выводы, устанавливать межпредметные и внутрипредметные связи, творчески применяет полученные знания в незнакомой ситуации.

3. Отсутствие ошибок и недочётов при воспроизведении изученного материала, при устных ответах устранение отдельных неточностей с помощью дополнительных вопросов учителя, соблюдение культуры письменной и устной речи, правил оформления письменных работ.

Оценка "4":

1. Знание всего изученного программного материала.

2. Умений выделять главные положения в изученном материале, на основании фактов и примеров обобщать, делать выводы, устанавливать внутрипредметные связи, применять полученные знания на практике.

3. Незначительные (негрубые) ошибки и недочёты при воспроизведении изученного материала, соблюдение основных правил культуры письменной и устной речи, правил оформления письменных работ.

Оценка "3" (уровень представлений, сочетающихся с элементами научных понятий): 

1. Знание и усвоение материала на уровне минимальных требований программы, затруднение при самостоятельном воспроизведении, необходимость незначительной помощи преподавателя.

2. Умение работать на уровне воспроизведения, затруднения при ответах на видоизменённые вопросы.

3. Наличие грубой ошибки, нескольких негрубых при воспроизведении изученного материала, незначительное несоблюдение основных правил культуры письменной и устной речи, правил оформления письменных работ.

Оценка "2":

1. Знание и усвоение материала на уровне ниже минимальных требований программы, отдельные представления об изученном материале.

2. Отсутствие умений работать на уровне воспроизведения, затруднения при ответах на стандартные вопросы.

3. Наличие нескольких грубых ошибок, большого числа негрубых при воспроизведении изученного материала, значительное несоблюдение основных правил культуры письменной и устной речи, правил оформления письменных работ.

4.Ставится за полное незнание изученного материала, отсутствие элементарных умений и навыков.

Устный ответ.

Оценка "5" ставится, если ученик:

1) Показывает глубокое и полное знание и понимание всего объёма программного материала; полное понимание сущности рассматриваемых понятий, явлений и закономерностей, теорий, взаимосвязей;

2) Умеет составить полный и правильный ответ на основе изученного материала; выделять главные положения, самостоятельно подтверждать ответ конкретными примерами, фактами; самостоятельно и аргументировано делать анализ, обобщения, выводы. Устанавливать межпредметные (на основе ранее приобретенных знаний) и внутрипредметные связи, творчески применять полученные знания в незнакомой ситуации. Последовательно, чётко, связно, обоснованно и безошибочно излагать учебный материал; давать ответ в логической последовательности с использованием принятой терминологии; делать собственные выводы; формулировать точное определение и истолкование основных понятий, законов, теорий; при ответе не повторять дословно текст учебника; излагать материал литературным языком; правильно и обстоятельно отвечать на дополнительные вопросы учителя. Самостоятельно и рационально использовать наглядные пособия, справочные материалы, учебник, дополнительную литературу, первоисточники; применять систему условных обозначений при ведении записей, сопровождающих ответ; использование для доказательства выводов из наблюдений и опытов;

3) Самостоятельно, уверенно и безошибочно применяет полученные знания в решении проблем на творческом уровне; допускает не более одного недочёта, который легко исправляет по требованию учителя; имеет необходимые навыки работы с приборами, чертежами, схемами и графиками, сопутствующими ответу; записи, сопровождающие ответ, соответствуют требованиям.

Оценка "4" ставится, если ученик:

1) Показывает знания всего изученного программного материала. Даёт полный и правильный ответ на основе изученных теорий; незначительные ошибки и недочёты при воспроизведении изученного материала, определения понятий дал неполные, небольшие неточности при использовании научных терминов или в выводах и обобщениях из наблюдений и опытов; материал излагает в определенной логической последовательности, при этом допускает одну негрубую ошибку или не более двух недочетов и может их исправить самостоятельно при требовании или при небольшой помощи преподавателя; в основном усвоил учебный материал; подтверждает ответ конкретными примерами; правильно отвечает на дополнительные вопросы учителя.

2) Умеет самостоятельно выделять главные положения в изученном материале; на основании фактов и примеров обобщать, делать выводы, устанавливать внутрипредметные связи. Применять полученные знания на практике в видоизменённой ситуации, соблюдать основные правила культуры устной речи и сопровождающей письменной, использовать научные термины;

3) Не обладает достаточным навыком работы со справочной литературой, учебником, первоисточниками (правильно ориентируется, но работает медленно). Допускает негрубые нарушения правил оформления письменных работ.

Оценка "3" ставится, если ученик:

1. усвоил основное содержание учебного материала, имеет пробелы в усвоении материала, не препятствующие дальнейшему усвоению программного материала;

2. материал излагает несистематизированно, фрагментарно, не всегда последовательно;

3. показывает недостаточную сформированность отдельных знаний и умений; выводы и обобщения аргументирует слабо, допускает в них ошибки.

4. допустил ошибки и неточности в использовании научной терминологии, определения понятий дал недостаточно четкие;

5. не использовал в качестве доказательства выводы и обобщения из наблюдений, фактов, опытов или допустил ошибки при их изложении;

6. испытывает затруднения в применении знаний, необходимых для решения задач различных типов, при объяснении конкретных явлений на основе теорий и законов, или в подтверждении конкретных примеров практического применения теорий;

7. отвечает неполно на вопросы учителя (упуская и основное), или воспроизводит содержание текста учебника, но недостаточно понимает отдельные положения, имеющие важное значение в этом тексте;

8. обнаруживает недостаточное понимание отдельных положений при воспроизведении текста учебника (записей, первоисточников) или отвечает неполно на вопросы учителя, допуская одну-две грубые ошибки.

Оценка "2" ставится, если ученик:

1. не усвоил и не раскрыл основное содержание материала;

2. не делает выводов и обобщений.

3. не знает и не понимает значительную или основную часть программного материала в пределах поставленных вопросов;

4. или имеет слабо сформированные и неполные знания и не умеет применять их к решению конкретных вопросов и задач по образцу;

5. или при ответе (на один вопрос) допускает более двух грубых ошибок, которые не может исправить даже при помощи учителя.

6. не может ответить ни на один из поставленных вопросов;

7 полностью не усвоил материал.

Примечание. 
По окончанию устного ответа учащегося педагогом даётся краткий анализ ответа, объявляется мотивированная оценка. Возможно привлечение других учащихся для анализа ответа, самоанализ, предложение оценки.

Оценка самостоятельных письменных и контрольных работ.

Оценка "5" ставится, если ученик:

1. выполнил работу без ошибок и недочетов;

2. допустил не более одного недочета.

Оценка "4" ставится, если ученик выполнил работу полностью, но допустил в ней:

1. не более одной негрубой ошибки и одного недочета;

2. или не более двух недочетов.

Оценка "3" ставится, если ученик правильно выполнил не менее половины работы или допустил:

1. не более двух грубых ошибок;

2. или не более одной грубой и одной негрубой ошибки и одного недочета;

3. или не более двух-трех негрубых ошибок;

4. или одной негрубой ошибки и трех недочетов;

5 или при отсутствии ошибок, но при наличии четырех-пяти недочетов.

Оценка "2" ставится, если ученик:

1. допустил число ошибок и недочетов превосходящее норму, при которой может быть выставлена оценка "3";

2. или если правильно выполнил менее половины работы;

3. не приступал к выполнению работы;

4. или правильно выполнил не более 10 % всех заданий.

Примечание. 
1) Учитель имеет право поставить ученику оценку выше той, которая предусмотрена нормами, если учеником оригинально выполнена работа.

2) Оценки с анализом доводятся до сведения учащихся, как правило, на последующем уроке, предусматривается работа над ошибками, устранение пробелов.

При оценке знаний, умений и навыков учащихся следует учитывать все ошибки (грубые и негрубые) и недочеты.

Грубыми считаются следующие ошибки:

1) незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;

2) незнание наименований единиц измерения;

3) неумение выделить в ответе главное;

4) неумение применять знания для решения задач и объяснения явлений;

5) неумение делать выводы и обобщения;

6) неумение читать и строить графики и принципиальные схемы;

7) неумение подготовить установку или лабораторное оборудование, провести опыт, наблюдения, необходимые расчеты или использовать полученные данные для выводов;

8) неумение пользоваться первоисточниками, учебником и справочниками;

9) нарушение техники безопасности;

10) небрежное отношение к оборудованию, приборам, материалам.

К негрубым ошибкам следует отнести:

1) неточность формулировок, определений, понятий, законов, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного-двух из этих признаков второстепенными;

2) ошибки в условных обозначениях на принципиальных схемах, неточность графика (например, изменение угла наклона) и др.

3) нерациональный метод решения задачи или недостаточно продуманный план устного ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);

4) нерациональные методы работы со справочной и другой литературой.

Недочетами являются:

1) нерациональные приемы вычислений и преобразований, выполнения опытов, наблюдений, заданий;

2) небрежное выполнение записей, чертежей, схем, графиков;

3) орфографические и пунктуационные ошибки.

КРИТЕРИИ И НОРМЫ ОЦЕНКИ ЗУН ОБУЧАЮЩИХСЯ

Учитель, опираясь на эти рекомендации, оценивает знания и умения учащихся с учетом их индивидуальных особенностей.

1. Содержание и объем материала, подлежащего проверке, определяется программой по математике для средней школы. При проверке усвоения этого материала следует выявлять полноту, прочность усвоения учащимися теории применять ее на практике в знакомых и незнакомых ситуациях.

2. Основными формами проверки знаний и умений учащихся по математике в средней школе письменная контрольная работа и устный опрос.

При оценке письменных и устных ответов учитель в первую очередь учитывает показанные учащимися знания и умения (их полноту, глубину, прочность, использование в различных ситуациях). Оценка зависит также от наличия и характера погрешностей, допущенных учащимися.

1. Среди погрешностей выделяются ошибки и недочеты:

Погрешность считается ошибкой, если она свидетельствует о том, что ученик не овладел знаниями, умениями, указанными в программе.

К недочетам относятся погрешности, свидетельствующие о недостаточно полном или недостаточно прочном усвоении основных знаний, умений или об отсутствии знаний, не считающихся в соответствии с программой основными. Недочетами также являются: погрешности, которые не привели к искажению смысла полученного учеником задания или способа его выполнения; неаккуратная запись; небрежное выполнение чертежа.

Граница между ошибками и недочетами является в некоторой степени условной. При одних обстоятельствах допущенная учащимися погрешность может рассматриваться учителем как ошибка, в другое время и при других обстоятельствах – как недочет.

1. Задания для устного и письменного опроса учащихся состоят из теоретических вопросов и задач.

Ответ не теоретический вопрос считается безупречным, если по своему содержанию полностью соответствует вопросу, содержит все необходимые теоретические факты и обоснованные выводы, а устное изложение и письменная запись ответа математически грамотны и отличаются последовательностью и аккуратностью.

Решение задачи считается безупречным, если правильно выбран способ решения, само решение сопровождается необходимыми объяснениями, верно выполнены нужные вычисления и преобразования, получен верный ответ, последовательно и аккуратно записано решение.

1. Оценка ответа учащегося при устном и письменном опросе проводится по пятибалльной системе, т.е. за ответ выставляется одна из отметок: 5 («отлично»), 4 («хорошо»), 3 («удовлетворительно»), 2 («неудовлетворительно»), 1 («плохо»).

Оценка устных ответов учащихся

Ответ оценивается отметкой «5», если ученик:

- полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;

- изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;

- правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;

- показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;

- продемонстрировал усвоение ранее изученных сопутствующих вопросов, сформированность и устойчивость используемых при ответе умений и навыков;

- отвечал самостоятельно, без наводящих вопросов учителя;

- возможны одна-две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.

Ответ оценивается отметкой «4», если удовлетворяет в основном, требованиям на оценку «5», но при этом имеет один из недостатков:

- в изложении допущены небольшие пробелы, не исказившие математическое содержание ответа;

- допущены один-два недочетов при освещении основного содержании ответа, исправленные после замечания учителя;

- допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.

Отметка «3» ставится в следующих случаях:

- неполно раскрыто содержание материала (содержание изложено элементарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, недостаточные для дальнейшего усвоения программного материала (определенные «Требованиями к математической подготовки учащихся» в настоящей программе по математике);

- имелись затруднения или допущены ошибки в определении понятий, использовании математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;

- ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;

- при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.

Отметка «2» ставится в следующих случаях:

- не раскрыто основное содержание учебного материала;

- обнаружено незнание или непонимание учеником, большей или наиболее важной части учебного материала;

- допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.

Отметка «1» ставится если:

- ученик обнаружил полное незнание и непонимание изучаемого материала или не смог ответить ни на один из поставленных вопросов по изучаемому материалу.

Оценка письменных и контрольных работ учащихся

Отметка «5» ставится если:

- работа выполнена полностью;

- в логических рассуждениях и обосновании решения нет пробелов ошибок;

- в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнаний или непонимания учебного материала).

Отметка «4» ставится в следующих случаях:

- работа выполнена полностью, но обоснования шагов решения недостаточно (если умения обосновывать рассуждения не являлось специальным объектом проверки);

- допущена одна ошибка или есть две-три недочетов в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).

Отметка «3» ставится если:

- допущена более одной ошибки или более двух-трех недочетов в выкладках, чертежах или графиках, но учащийся обладает обязательными умениями по проверяемой теме.

Отметка «2» ставится если:

- допущена существенные ошибки, показавшие, что учащийся не обладает обязательными умениями по данной теме в полной мере.

Отметка «1» ставится если:

- работа показала полное отсутствие у учащегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.

6. Учитель может повысить:

- отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии учащегося;

- за решение более сложной задачи или ответ на более сложный вопрос, предложенные учащемуся дополнительно после выполнения им каких-либо других заданий.

Общая классификация ошибок.

При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.

Грубыми считаются ошибки:

• незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;

• незнание наименований единиц измерения;

• неумение выделить в ответе главное;

• неумение применять знания, алгоритмы для решения задач;

• неумение делать выводы и обобщения;

• неумение читать и строить графики;

• неумение пользоваться первоисточниками, учебником и справочниками;

• потеря корня или сохранение постороннего корня;

• отбрасывание без объяснений одного из них;

• равнозначные им ошибки;

• вычислительные ошибки, если они не являются опиской;

• логические ошибки.

К негрубым ошибкам следует отнести:

• неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;

• неточность графика;

• нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);

• нерациональные методы работы со справочной и другой литературой;

• неумение решать задачи, выполнять задания в общем виде.

Недочетами являются:

• нерациональные приемы вычислений и преобразований;

• небрежное выполнение записей, чертежей, схем, графиков.

Опираясь на эти рекомендации, учитель оценивает знания и умения учащихся с учетом их индивидуальных особенностей.

1. Содержание и объем материала, подлежащего проверке, определяется программой. При проверке усвоения материала нужно выявлять полноту, прочность усвоения учащимися теории и умения применять ее на практике в знакомых и незнакомых ситуациях.

2. Основными формами проверки знаний и умений учащихся по математике являются письменная контрольная работа и устный опрос.

При оценке письменных и устных ответов учитель в первую очередь учитывает показанные учащимися знания и умения. Оценка зависит также от наличия и характера погрешностей, допущенных учащимися.

3. Среди погрешностей выделяются ошибки и недочеты. Погрешность считается ошибкой, если она свидетельствует о том, что ученик не овладел основными знаниями, умениями, указанными в программе.

К недочетам относятся погрешности, свидетельствующие о недостаточно полном или недостаточно прочном усвоении основных знаний и умений или об отсутствии знаний, не считающихся в программе основными. Недочетами также считаются: погрешности, которые не привели к искажению смысла полученного учеником задания или способа его выполнения; неаккуратная запись; небрежное выполнение чертежа.

Граница между ошибками и недочетами является в некоторой степени условной. При одних обстоятельствах допущенная учащимися погрешность может рассматриваться учителем как ошибка, в другое время и при других обстоятельствах - как недочет.

4. Задания для устного и письменного опроса учащихся теоретических вопросов и задач.

Ответ на теоретический вопрос считается безупречным, если по своему содержанию полностью соответствует вопросу, содержит все необходимые теоретические факты и обоснованные выводы, а его изложение и письменная запись математически грамотны и отличаются последовательностью и аккуратностью.

Решение задачи считается безупречным, если правильно выбран способ решения, само решение сопровождается необходимыми объяснениями, верно выполнены нужные вычисления и преобразования, получен верный ответ, последовательно и аккуратно записано решение.

Оценка ответа учащегося при устном и письменном опросе проводится по пятибалльной системе, То есть за ответ выставляется одна из отметок: 1 (плохо), 2 (неудовлетворительно), 3 (удовлетворительно), 4 (хорошо), 5 (отлично).

Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии учащегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные учащемуся дополнительно после выполнения им заданий. Итоговые отметки (за тему, четверть, курс) выставляются по состоянию знаний на конец этапа обучения с учетом текущих отметок.

40