|
Актуализация знаний
|
Давайте вспомним, с какими основными понятиями и определениями вы познакомились при изучении темы
Вернемся в 10 класс. Мы учились решать задачи на поиск количества путей в графе и анализ информационных моделей. Это задания № 3 и15 в ЕГЭ по информатике. Давайте вспомним, как мы это делали. Для этого выполним следующие задание:.
|
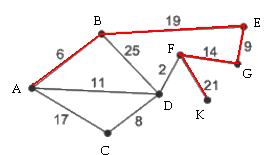
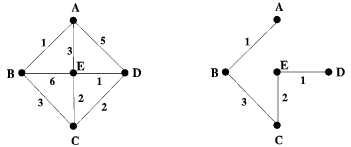
  На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся
сведения о длинах этих дорог
(в километрах).
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова длина дороги из пункта Б в пункт Д.
|
|
(Ответ 8)
Между населёнными пунктами A, B, C, D, E, F, Z построены дороги с односторонним движением. В таблице указана протяжённость каждой дороги. Отсутствие числа в таблице означает, что прямой дороги между пунктами нет. Например, из A в B есть дорога длиной 4 км, а из B в A дороги нет.
|
|
A
|
B
|
C
|
D
|
E
|
F
|
Z
|
|
A
|
|
4
|
6
|
|
|
|
30
|
|
B
|
|
|
3
|
4
|
|
|
|
|
C
|
|
|
|
11
|
|
|
27
|
|
D
|
|
|
|
|
4
|
7
|
10
|
|
E
|
|
|
|
|
|
4
|
8
|
|
F
|
|
|
|
|
|
|
2
|
|
Z
|
29
|
|
|
|
|
|
|
Сколько существует таких маршрутов из A в Z, которые проходят через 6 и более населенных пунктов? Пункты A и Z при подсчете учитывать. Два раза проходить через один пункт нельзя. (Ответ 5)
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, К, Л, М, Н, П, Р, С, Х, Т. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей, ведущих из города А в город Т?

(Ответ: 66)
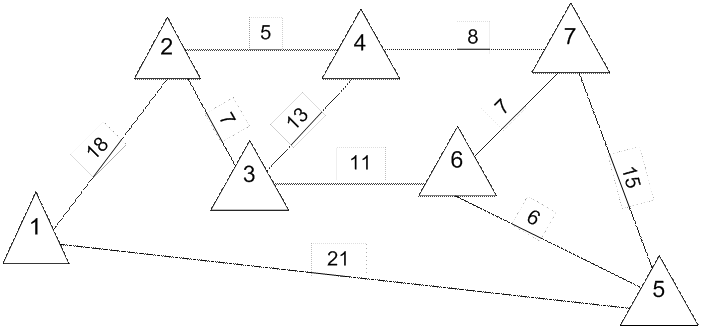
  4. . На рисунке – схема дорог, связывающих города. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей, ведущих из города 1 в город 7? 4. . На рисунке – схема дорог, связывающих города. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей, ведущих из города 1 в город 7?
|
|
|
|
постановка цели деятельности (постановка учебной задачи)
|
Запишем тему урока: « Поиск кратчайших путей в графе»
Виды алгоритмов:
- «жадный алгоритм» - алгоритм состоит в том, чтобы на каждом шаге многоходового процесса выбирать наилучший в данный момент вариант, не думая о том, что впоследствии этот выбор может привести к худшему решению
(алгоритм, который, на каждом шагу принимают локально оптимальное решение, не заботясь о том, что будет дальше)
- сформулируйте алгоритм Прима-Крускала - это «жадный» алгоритм, который всегда приводит к правильному решению. В теории графов – это построение минимального основного дерева, т.е. дерева, связывающего все вершины
1.начальное дерево – пустое
2.на каждом шаге добавляется ребро минимального веса, которое ещё не входит в дерево и не приводит к появлению цикла
- в чем заключается алгоритм Дейкстра? - алгоритм, нахождения кратчайшего расстояния от одной из вершин графа до всех остальных
Вывод: не всякий алгоритм дает оптимальное решение.
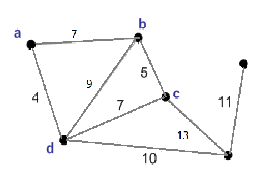
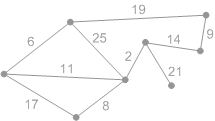
Решим следующую задачу: граф рисую на доске
требуется найти кратчайшее расстояние от 1-й вершины до 6 используя «жадный алгоритм».
1) Жадный алгоритм

Жадные алгоритмы – это общее название подхода к решению задач оптимизации. Вопрос: в какой области науки решают задачи по оптимизации?
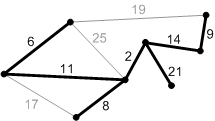
2)Алгоритм Прима-Крускала

Общая длина равна 33.
3)
|
1
|
2
|
3
|
4
|
5
|
6
|
|
0
|
¥
|
¥
|
¥
|
¥
|
¥
|
|
|
7
|
9
|
¥
|
¥
|
14
|
|
|
|
9
|
22
|
¥
|
14
|
|
|
|
|
20
|
¥
|
11
|
|
|
|
|
20
|
20
|
|
|
|
|
|
|
20
|
|

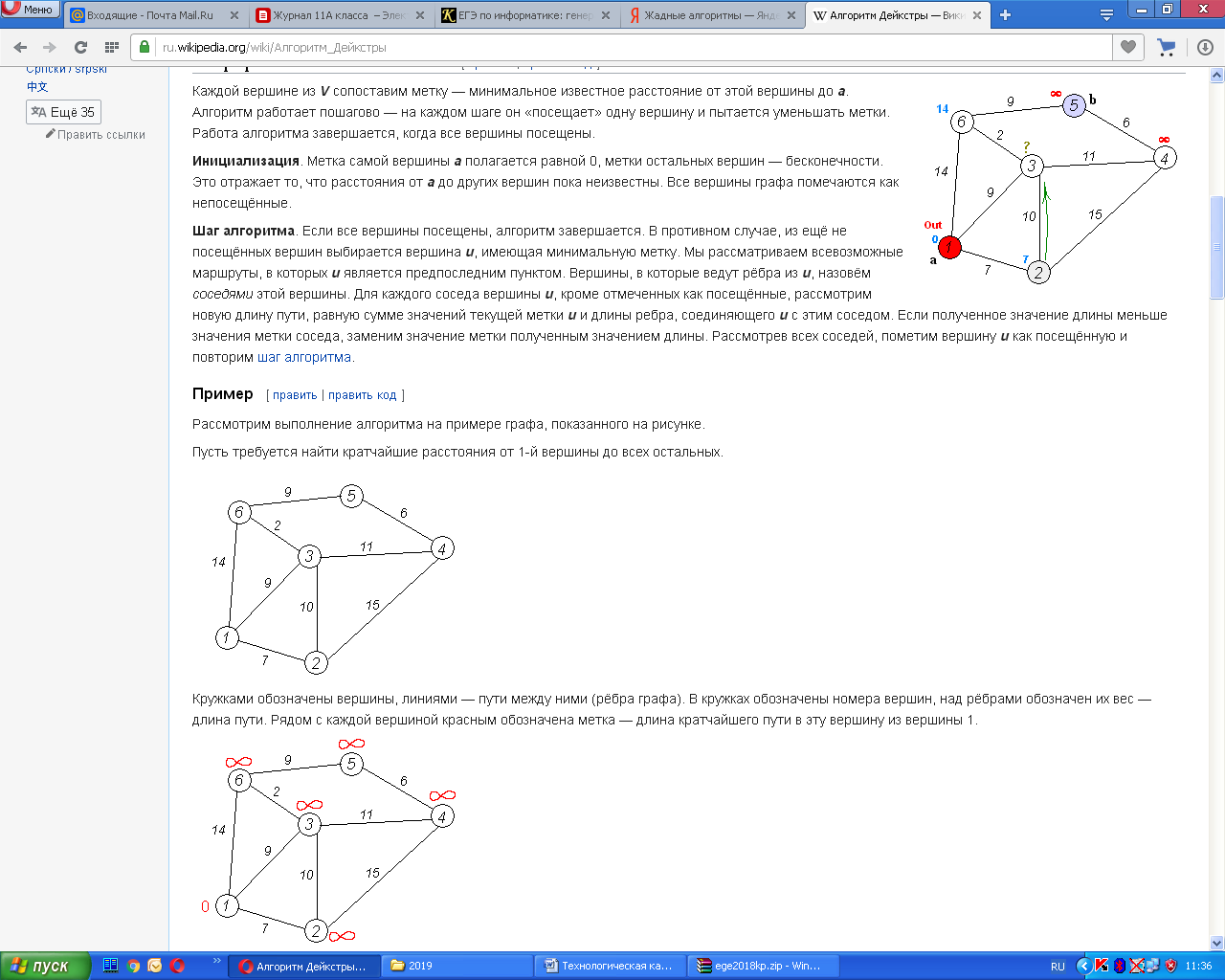
Результат работы алгоритма: кратчайший путь от вершины 1 до 2-й составляет 7, до 3-й — 9, до 4-й — 20, до 5-й — 20, до 6-й — 11.
Займемся выводом кратчайшего пути. Мы знаем длину пути для каждой вершины, и теперь будем рассматривать вершины с конца. Рассматриваем конечную вершину (в данном случае — вершина 5), и для всех вершин, с которой она связана, находим длину пути, вычитая вес соответствующего ребра из длины пути конечной вершины.
Так, вершина 5 имеет длину пути 20. Она связана с вершинами 6 и 4.
Для вершины 6 получим вес 20 — 9 = 11 (совпал).
Для вершины 4 получим вес 20 — 6 = 14 (не совпал).
Если в результате мы получим значение, которое совпадает с длиной пути рассматриваемой вершины (в данном случае — вершина 6), то именно из нее был осуществлен переход в конечную вершину. Отмечаем эту вершину на искомом пути.
Далее определяем ребро, через которое мы попали в вершину 6. И так пока не дойдем до начала.
Если в результате такого обхода у нас на каком-то шаге совпадут значения для нескольких вершин, то можно взять любую из них — несколько путей будут иметь одинаковую длину.
|










 4. . На рисунке – схема дорог, связывающих города. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей, ведущих из города 1 в город 7?
4. . На рисунке – схема дорог, связывающих города. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей, ведущих из города 1 в город 7?


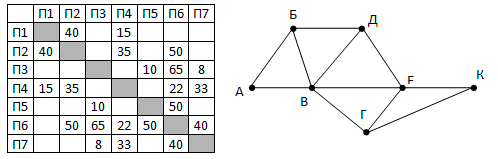 На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся
На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся 
 4. . На рисунке – схема дорог, связывающих города. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей, ведущих из города 1 в город 7?
4. . На рисунке – схема дорог, связывающих города. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей, ведущих из города 1 в город 7?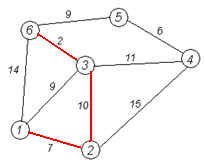
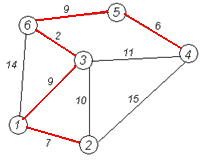

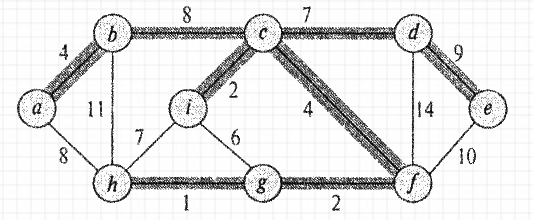

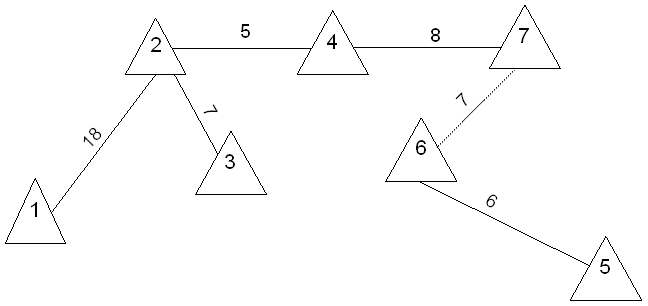
 Задание: используя алгоритм Прима-Крускала найдите на графе минимальное основное дерево. Является ли оно универсальным?
Задание: используя алгоритм Прима-Крускала найдите на графе минимальное основное дерево. Является ли оно универсальным?