![]() Урок по теме: "Показательная функция" 10-й класс
Урок по теме: "Показательная функция" 10-й класс
Тип урока: урок повторения и обобщения
Цель урока: повторить и обобщить свойства показательной функции, а также методы решения показательных уравнений и неравенств.
Образовательные задачи:
закрепление знаний, умений и навыков учащихся по данной теме;
применение свойств функции при решении уравнений и неравенств;
контроль и самоконтроль знаний и умений учащихся при решении
самостоятельной работы;
Развивающие задачи:
ситуации;
излагать мысли;
Воспитательные задачи:
умения работать в коллективе, взаимопомощи, культуры общения;
формирование у учащихся познавательного интереса к математике;
воспитание таких качеств характера, как настойчивость в достижении цели.
Подготовка к уроку: создание компьютерной презентации; подбор заданий с использованием свойств показательной функции, показательных уравнений и неравенств.
которые являются весьма популярными заданиями во всех вариантах тестов ЕГЭ и традиционно считаются трудной темой школьного курса математики.
Оборудование: Компьютеры, презентация по теме «Показательная функция»; индивидуальные задания на компьютере.
Структура урока:
Организационный момент. Постановка цели урока.
Историческая справка.
Актуализация опорных знаний. Блиц – опрос.
Число е (экспонента).
Применение показательной функции в природе и технике.
Выполнение практической работы.
Подведение итогов.
ХОД УРОКА:
Организационный момент. Постановка цели урока.
Сегодня на уроке мы повторим и обобщим знания, связанные с понятием показательной функции, а также с понятием функции вообще. Проверим умение решать показательные уравнения и неравенства. Рассмотрим практическую значимость показательной функции, а также определим уровень усвоения материала по данной теме.
Задания с использованием свойств показательной функции, показательные уравнения и неравенства являются весьма популярными заданиями во всех вариантах тестов ЕГЭ и традиционно считаются трудной темой школьного курса математики.
Учащиеся записывают число и тему урока в тетради. На экран выводится тема урока «Показательная функция» (Презентация, слайд 1).
«...Именно функция является тем средством
математического языка, которое позволяет
описывать процессы движения, изменения,
присущие природе».
Г.Галилей
(слайд 2)
Кто может ответить на вопрос, а что же такое функция? (Определение «функции»)
Функция – одно из основных математических общенаучных понятий, зависимость между переменными величинами. (слайд 3)
Концентрация внимания:
Мне попалась на глаза интересная задача. Подумайте, можно ли по её условию составить уравнение.
Задача: Если шофёру господина министра 40 лет 3 месяца и 12 дней, а мост в городе Квебек (Канада) имеет длину 577 метров, то на скольких желтках нужно замесить лапшу, чтобы накормить 6 человек различного возраста, если принять во внимание, что ширина полотна на железных дорогах Боснии составляет 0, 7 метра?
Можно ли по условию задачи составить функцию? (безусловно, нет) (слайд 4)
Почему? (Потому что величины, входящие в условие задачи, никак между собой не связаны. Ни одна из них, как мы говорим, не является функцией от другой).
Историческая справка.
Слово «функция» (от латинского function – исполнение, осуществление) в математике впервые употреблено немецким математиком В.Г.Лейбницем. (слайд 5)
Но сами функции и способы их задания фактически изучались людьми очень давно. Знаменитый древнегреческий историк Геродот в 425 году до нашей эры писал, что египетские цари, разделив землю между египтянами, брали ежегодный налог, пропорциональный площади занимаемого участка. Конечно, ни египетские цари, ни землевладельцы, ни сам Геродот не произносили слова “функция”, но ведь речь идёт о том, что каждому значению площади соответствовало некоторое значение налога. (слайд 7)
Хотя в древности функций не знали, но явления, которые мы сегодня описываем с их помощью, давно известны людям. (слайд8 )
Какие ещё понятия связаны с понятием функции?
(Даются определения:
(слайд 9)
Понятие переменной величины было введено в науку франц. Ученым и математиком Рене Декартом. (слайд10 )
Математика рассматривает абстрактные переменные величины, изучает различные законы их взаимосвязи, не углубляясь в природу задачи. (слайд11 )
Например, в соотношении у = х2 геодезист или геометр увидит зависимость площади квадрата от его стороны, а физик, авиаконструктор или кораблестроитель может усмотреть в нем зависимость силы у сопротивления воздуха или воды от скорости х движения.
(слайд12 )
Математика же изучает эту зависимость в отвлеченном виде, и она устанавливает, например, что увеличение х в 2 раза приведет к увеличению у в 4 раза, и это заключение может применяться в любой конкретной ситуации.
В школьном курсе изучается немало функций. Одной из самых важных является показательная функция y=ax, где a 0, a ≠ 1.
Графики показательной функции (Рисунок 1 и 2).
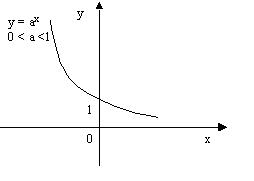
Рис. 1
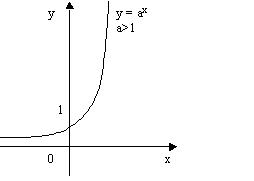
Рис. 2
Актуализация опорных знаний. Блиц – опрос.
Почему ее называют показательной?
Чем отличаются степенная и показательная функции?
Почему a 0?
Почему a ≠ 1?
Как ведет себя показательная функция при a 1?
Как ведет себя показательная функция при 0 a 1?
Еще 40 веков назад в египетском папирусе записан ряд. Про семь домов, где кошек 49, и каждая из них по 7 мышей съедает и тем всем столько зерен сохраняет, что мер 17000 составляет. Мы объяснили факт немножко, священна почему в Египте кошка.
О том еще известна нам легенда, что как-то у арабского царя
изобретатель шахматной доски, наверно потребовал за доску ту зерна. Причем за клетку первую – зерно, а за вторую – два просил изобретатель, за третью – снова больше раза в два, немало времени царь на подсчет потратил. Когда же подсчитали – прослезились: число двадцатизначно получилось! Хватило б зернами засеять нам всю сушу и миллионы лет пришлось зерно бы кушать.
Число е (экспонента).
Возведение в степень на немецком языке звучит - potenzie. Отсюда и происходит слово потенцировать.
А слово «показатель» на немецком языке звучит как Exponent.
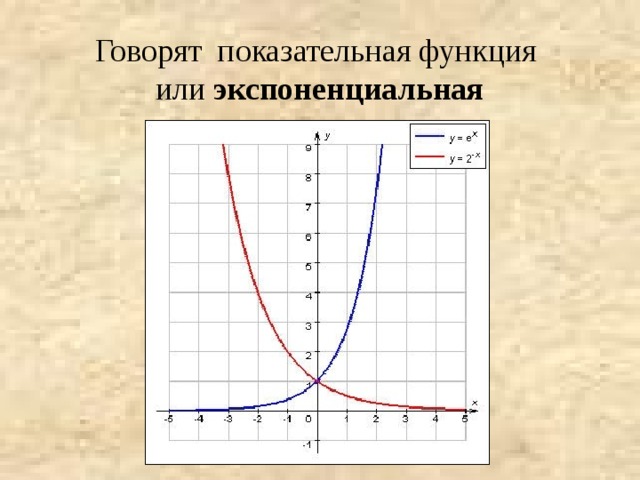
Число е (экспонента) (от лат. exponens — показывающий) - одна из важнейших постоянных в математике.
Говорят показательная кривая или (экспоненциальная) показательная функция.
Число е =  .
.
Обозначение e ввёл Леонард Эйлер в 1736 г. Он вычислил первые 23 знака этого числа в десятичной записи, а само число назвали в честь Непера «неперовым числом».
Число e играет особую роль в математическом анализе.
Показательная функция с основанием e, называется экспонентой и обозначается
y = ex.
Численно оно равно: e = 2,71828182845904523536...
Первые знаки числа e запомнить несложно: два, запятая, семь, два раза - год рождения Льва Толстого, сорок пять, девяносто, сорок пять.
Все знают, что такое ростовщик. Тот человек проценты брать привык.
Они встречались в Вавилоне древнем, где пятую часть «лихвы» взимали в среднем!
Пятнадцатый век – рожденье банков, дающих деньги людям под процент, тогда и встал вопрос довольно ярко о дробном показателе, сомненья нет. Его развили математик Штифель, Оресм, Шюке, затем Исаак Ньютон. И в завершении Бернулли Иоганном был термин «показательной» введен. На множестве всех чисел он ее нам ввел, как открыватель функции в историю вошел.
Итак, показательная функция не случайно родилась, в жизнь органически влилась и движением прогресса занялась.
Применение показательной функции в природе и технике.
Определить и воспроизвести идею составления ряда: 1 2 4 8 16 32 64 …
Нет ни одной области математики,
которая когда-нибудь не окажется применимой
к явлениям действительного мира.
Н.И. Лобачевский
Показательная функция, подобно линейной и квадратичной, очень часто реализуется в физических, биологических и иных законах. И это, конечно, не является случайностью. В жизни нередко приходится встречаться с такими фактами, когда скорость изменения какой-либо величины пропорциональна самой величине (размножение бактерий, ход химической реакции и т.д.). В этом случае рассматриваемая величина изменятся по закону: y = y0ax.
1. По закону показательной функции размножалось бы все живое на Земле, если бы для этого имелись благоприятные условия, т. е. не было естественных врагов и было вдоволь пищи. Доказательство тому – распространение в Австралии кроликов, которых там раньше не было. Достаточно было выпустить пару особей, как через некоторое время их потомство стало национальным бедствием.
2. Если бы все маковые зерна давали всходы, то через 5 лет число «потомков» одного растения равнялось бы 243 • 1015 или приблизительно 2000 растений на 1 м2 суши.
3. Потомство комнатных мух за лето только от одной самки может составить 8 • 1014. Эти мухи весили бы несколько миллионов тонн, а выстроенные в одну цепочку, они составили бы расстояние, большее, чем расстояние от Земли до Солнца. Потомство пары мух за 2 года имело бы массу, превышающую массу земного шара. И только благодаря сообществу животных и растений, когда увеличение одного вида влечет за собой рост количества его врагов, устанавливается динамическое равновесие в природе.
4. В природе, технике и экономике встречаются многочисленные процессы, в ходе которых значение величины меняется в одно и то же число раз, т. е. по закону показательной функции. Эти процессы называются процессами органического роста или органического затухания. Например, рост бактерий в идеальных условиях соответствует процессу органического роста; радиоактивный распад вещества – процессу органического затухания. Законам органического роста подчиняется рост вклада в Сберегательном банке, восстановление гемоглобина в крови, донора или раненого, потерявшего много крови, рост дрожжей, ферментов, микроорганизмов. Закон органического роста выражается формулой: N = N0ekt. По этому же закону изменяется количество древесины в дереве, что имеет большое значение для рационального ведения лесного хозяйства.
5. В природе и технике часто можно наблюдать процессы, которые подчиняются законам выравнивания, описываемым показательной функцией. Например, температура чайника изменяется со временем (согласно формуле Т = Т0 + (100 – Т0)е-kt. Процессы выравнивания также можно наблюдать при включении и выключении электрического тока в цепи при падении тел в воздухе с парашютом. В биологии процесс выравнивания встречается при разрушении адреналина в крови; о работе почек судят по их способности выводить радиоактивные вещества, количество которых уменьшается по показательному закону.
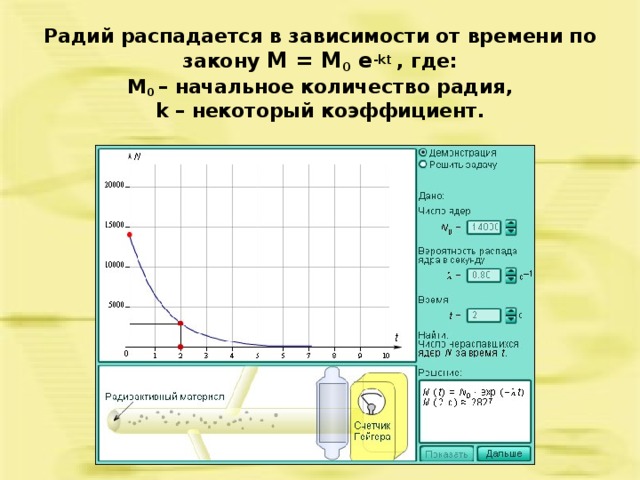
6. Радий распадается в зависимости от времени по закону М = М0 e-kt , где: М0 – начальное количество радия, k – некоторый коэффициент. Пользуясь этой формулой, ученые смогли подсчитать возраст Земли, то есть время, в течение которого радий смог распадаться нормально.
7. Вы все слышали о цепных реакциях, теорию которых в 20-х годах описал молодой химик Н.Н. Семенов, а потом развили ученые-атомщики. Как управлять этим процессов в мирных целях? На этот вопрос можно ответить только при помощи знаний о показательной функции.
8. Давление атмосферы, выраженное в миллиметрах ртутного столба, меняется по закону: 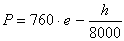 , где h – высота точки над уровнем моря (в м). Эту формулу используют геодезисты для барометрического инвелирования, то есть для определения разности высот над уровнем моря двух точек на земной поверхности.
, где h – высота точки над уровнем моря (в м). Эту формулу используют геодезисты для барометрического инвелирования, то есть для определения разности высот над уровнем моря двух точек на земной поверхности.
9. При прохождении света через мутную среду каждый слой этой среды поглощает строго определенную часть падающего на него света. Сила света I определяется по формуле: I = I0e-ks, где: s – толщина слоя, k – некоторый коэффициент, характеризующий мутную среду.
Подобный же закон будет характеризовать процесс поглощения газа соответствующей средой, изменение скорости ветра и т.п.
10. Закон охлаждения. Пусть Т1 – температура тела, Т0 – температура окружающей среды, где Т1Т0 , Тогда температура тела Т будет меняться по закону: Т = Т0 + (Т1 – Т0)е-kt, где k – некоторый коэффициент, зависящий от природы охлаждающего тела.
Многообразные применения показательной или экспоненциальной функции вдохновили английского поэта Элмера Брила на написание «Оды экспоненте», отрывок из которой гласит:
“…Ею порождено многое из того, что «достойно упоминания»,
Как говорили наши англосаксонские предки.
Могущество её порождений
Заранее обусловлено её собственной красотой и силой,
Ибо они суть физическое воплощение
Абстрактной идеи е.
Английские моряки любят и знают её
Под именем “Гунтер”.
Выполнение практической работы. (форма работы: индивидуальная).
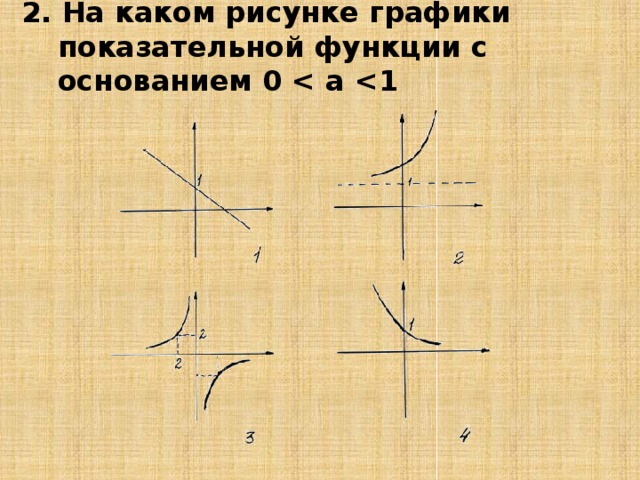
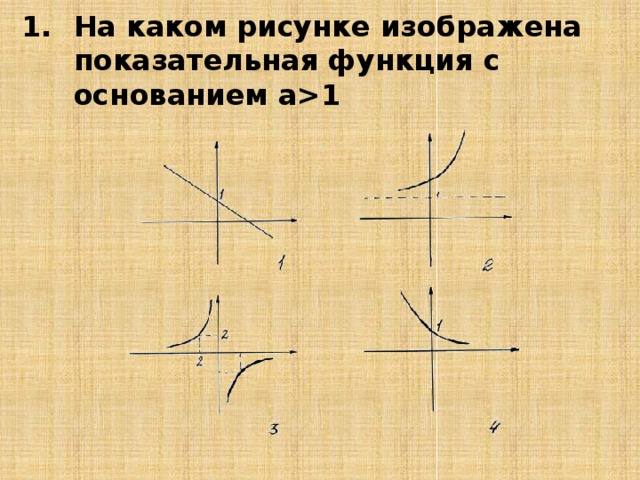
На каком рисунке показательной функции с основанием а1

2
2.
На каком рисунке графики показательной функции с основанием 0
4
2. Выберите верные утверждения (варианты ответов предложены на листках командам)
П.ф. имеет экстремумы
П.ф. принимает значение равное нулю.
П.Ф. принимает значение равное 1.
П.ф. принимает только положительное значение.
Какие из перечисленных ниже функций являются показательными:
у=2х; у=х2; у=5х; у=х -1; 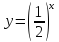 у=10-х.
у=10-х.
Какие из перечисленных показательных функций являются возрастающими, а какие убывающими:
у = (7,2)х; у=64-х; y=(1/3)x; y = -2х.
Решить уравнение:
32х + 1 – 9 = 0;
22х + 1 + 22х – 1 – 28 = 0;
Что больше 
Подведение итогов.
Значимость изучения функциональных зависимостей.
Сегодня мы проследили за функциональными зависимостями в окружающем мире. Оценили их роль в практической деятельности человека, убедились в необходимости изучения функции.
Дополнительные вопросы:
1) Если однолетнее растение дает 100 семян и из них прорастает половина, то за каждый год число растений увеличивается в 50 раз. Найти количество растений за n лет. Как изменяется время? Количество растений? (y = 50n)
2) Банк выплачивает дивиденды в размере 50 % годовых, т. е. за каждый год первоначальный капитал, равный а, увеличивается в 1,5 раза. Какую сумму вклада составит через n лет ? ( y = a · 1,5?)
3) Почему не бывает животных, какой угодно величины? Например, почему нет слонов в 3 раза большего роста, чем существует, но тех же пропорций? [20]
4







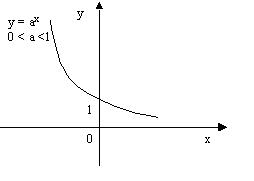

 .
.
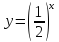 у=10-х.
у=10-х.













 0 , a ≠ 1 . при 0 при a 1" width="640"
0 , a ≠ 1 . при 0 при a 1" width="640"
 0 ? Почему a ≠ 1 ? Как ведет себя показательная функция при a 1 ? Как ведет себя показательная функция при 0 a 1 ?" width="640"
0 ? Почему a ≠ 1 ? Как ведет себя показательная функция при a 1 ? Как ведет себя показательная функция при 0 a 1 ?" width="640"

























 1" width="640"
1" width="640"