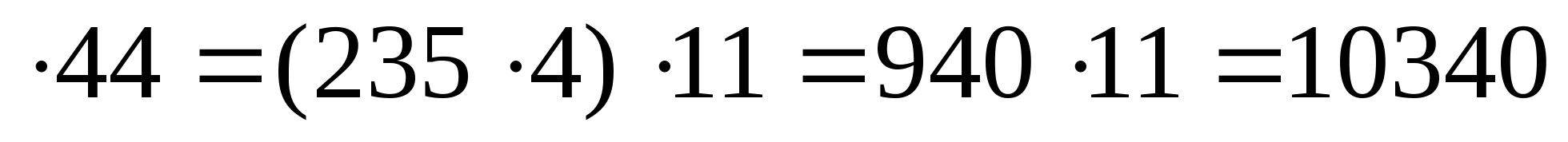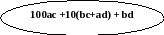Помощь выпускнику по подготовке к ЕНТ по математике

Помощь выпускнику по подготовке к ЕНТ по математике

I. Вычисляем быстро.

1. Умножение двузначных чисел (метод Ферроля).

Этот способ следует из тождества:

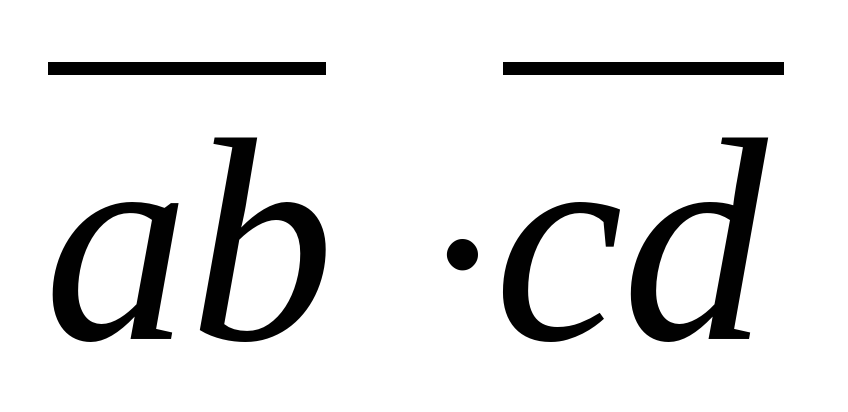=(10a+b) (10c+d) = 100ac + 10bc + 10ad + bd = 100ac +10(bc+ad) + bd

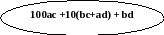
Получается алгоритм, который продемонстрируем на примере:

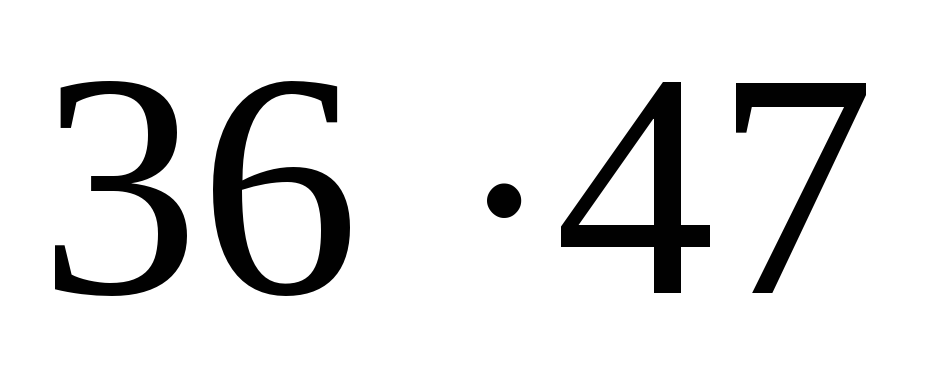
а) 6 = 42; два пишем и 4 запоминаем;

б) 6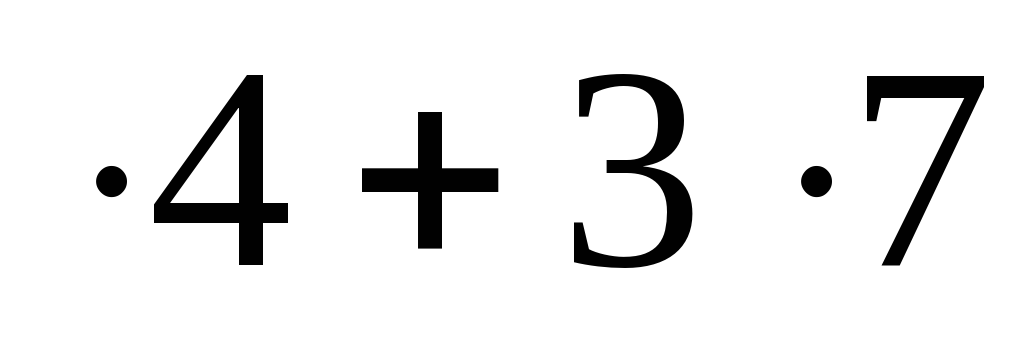 = 24 + 21 = 45, да ещё запоминали 4: 45 + 4 = 49; девять пишем и четыре запоминаем;

в) 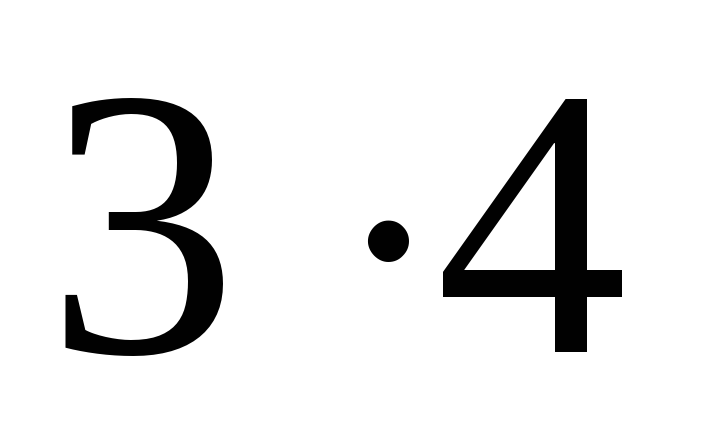= 12, да ещё запоминали 4: 12 + 4 = 16.

Таким образом, получаем 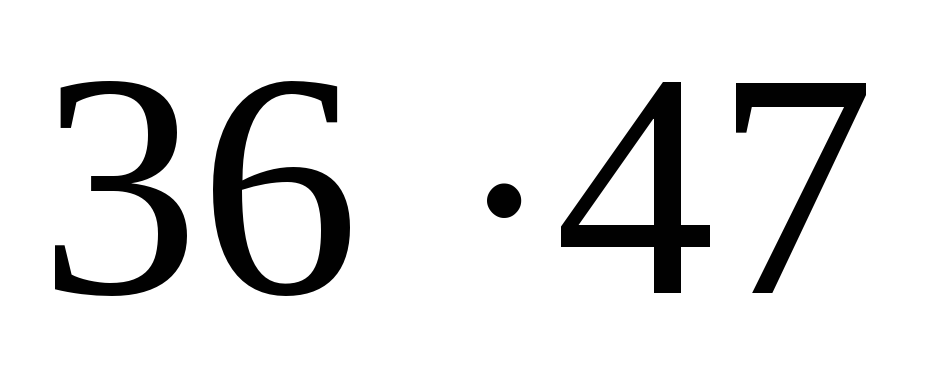= 1692.

• Методом Ферроля легко перемножать устно двузначные числа от 10 до 20.

Например, чтобы умножить 13 на 12, делаем так:

а) 3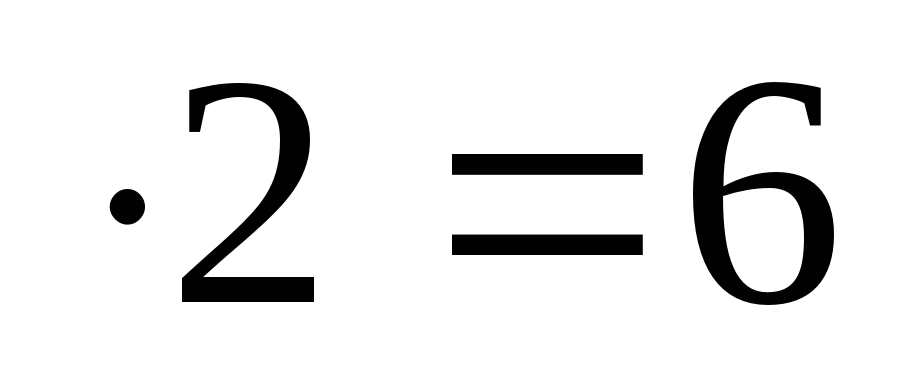 (единицы),

б) 3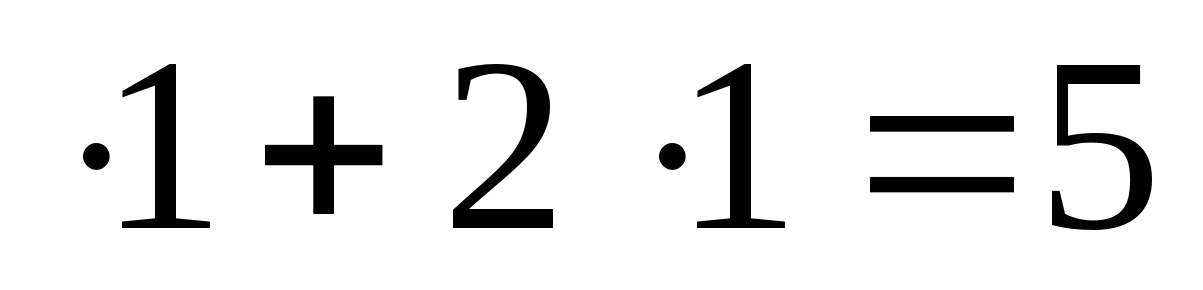 (десятки),

в) 1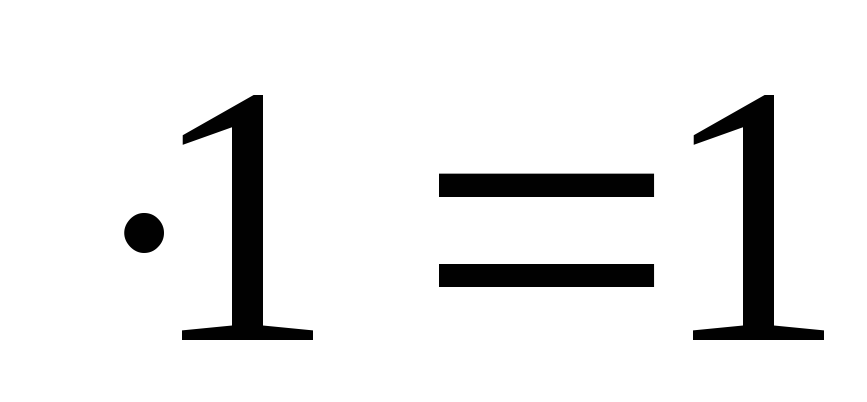 (сотни).

Получаем: .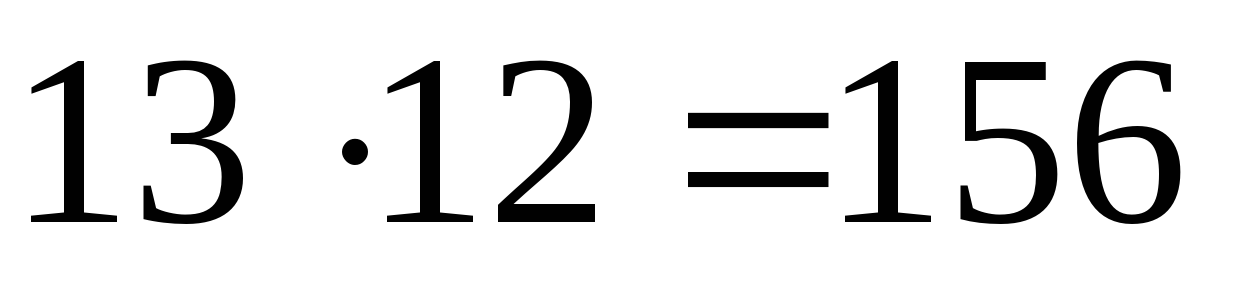

• Можно умножать и трехзначное число на двухзначное число.

Например: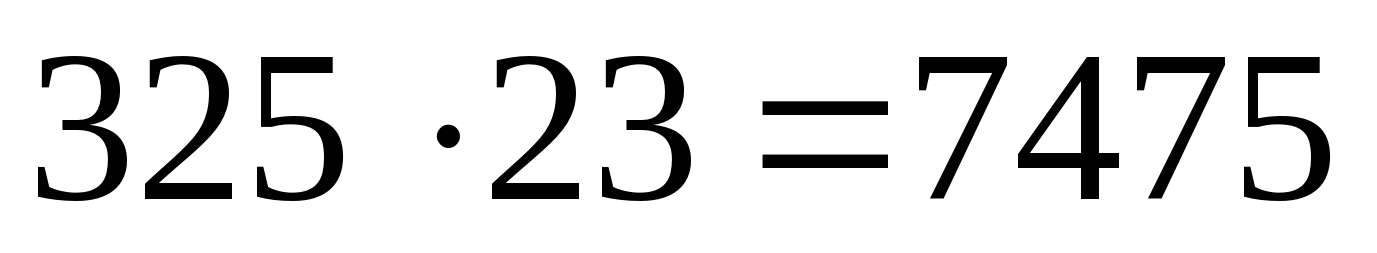

а) 5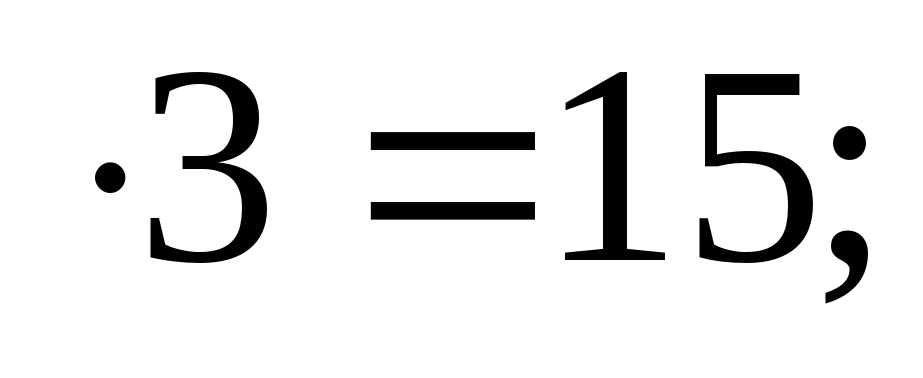 пишем пять, один запоминаем.

б) 3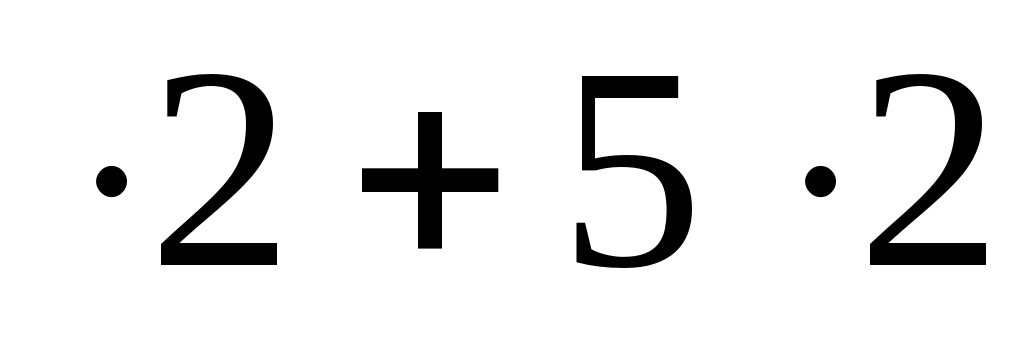 = 16; 16 + 1 = 17; пишем семь, один запоминаем.

в) 3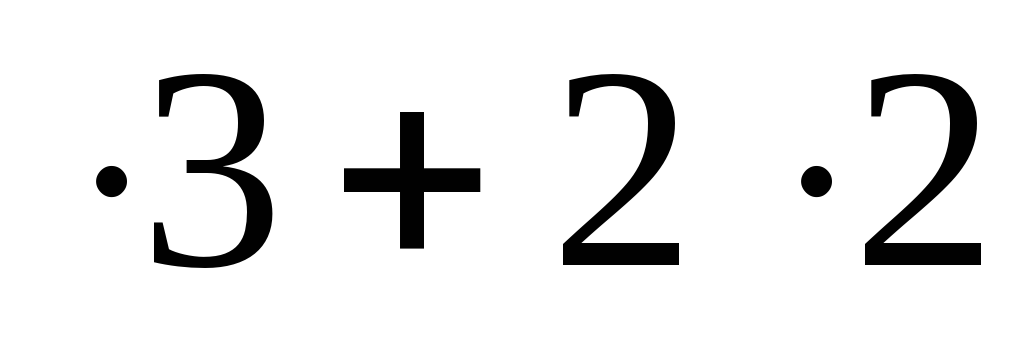 = 13; 13 + 1 =14; пишем четыре, один запоминаем.

г) 3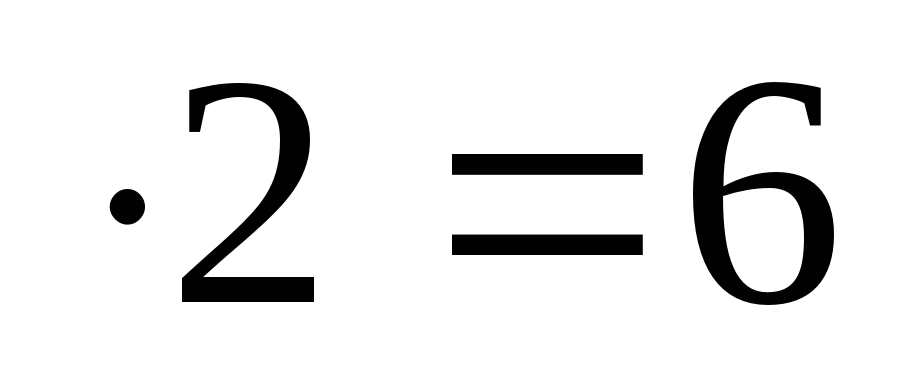; 6 + 1 = 7.

2. Рациональный метод возведения в квадрат двузначного числа.

Этот метод основывается на следующих рассуждениях:

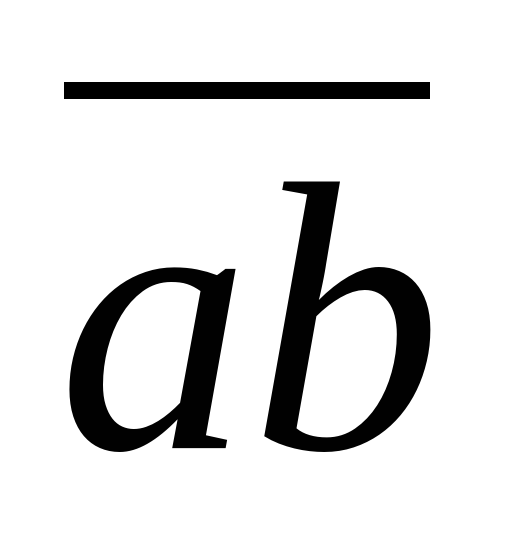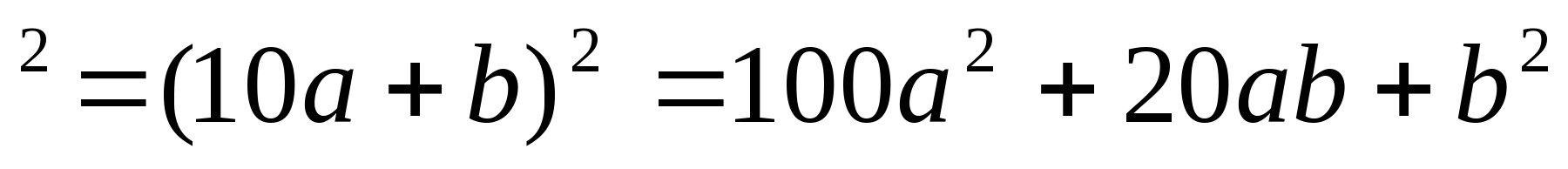()=100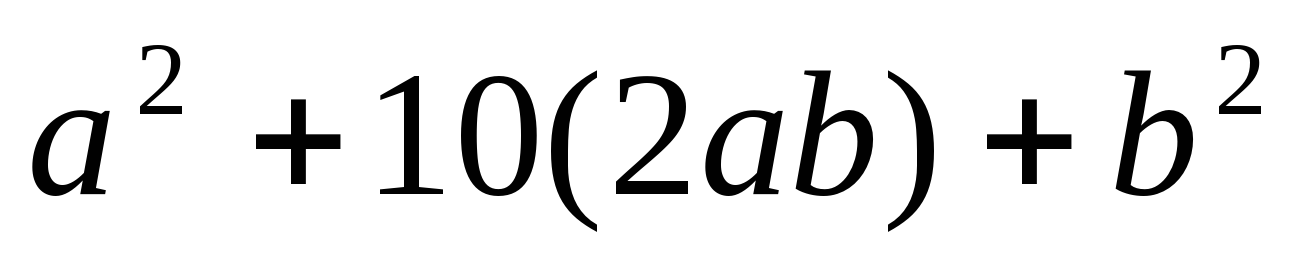

Например:

1) 53=2809.

а) 3,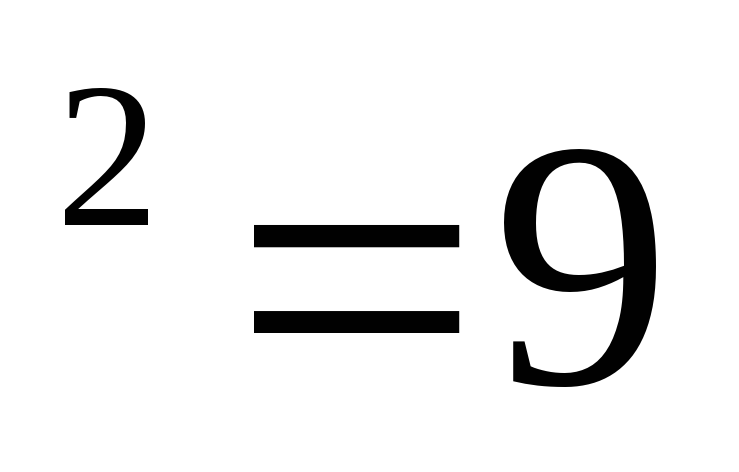

б) (5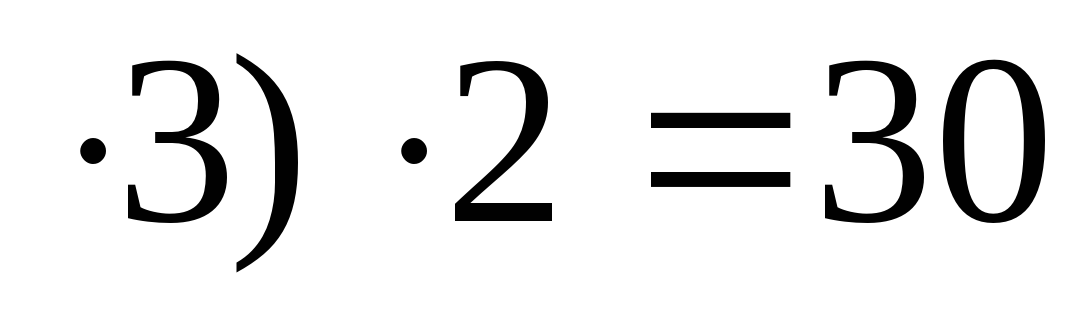; ноль пишем, три запоминаем;

в) 5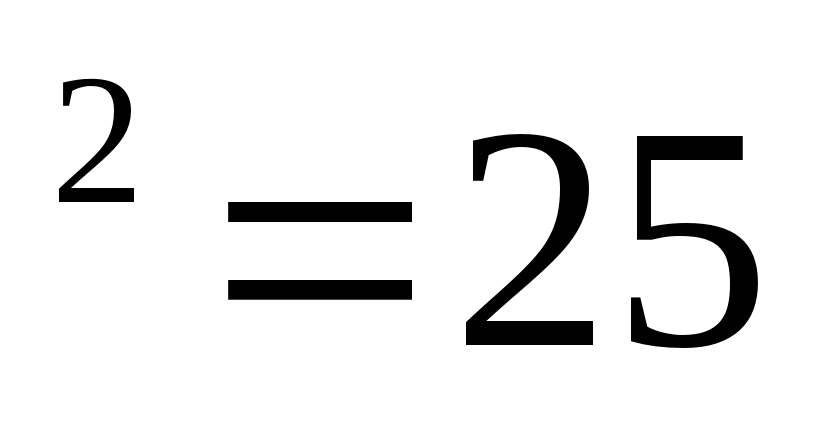; 25 + 3 = 28.

2) 64.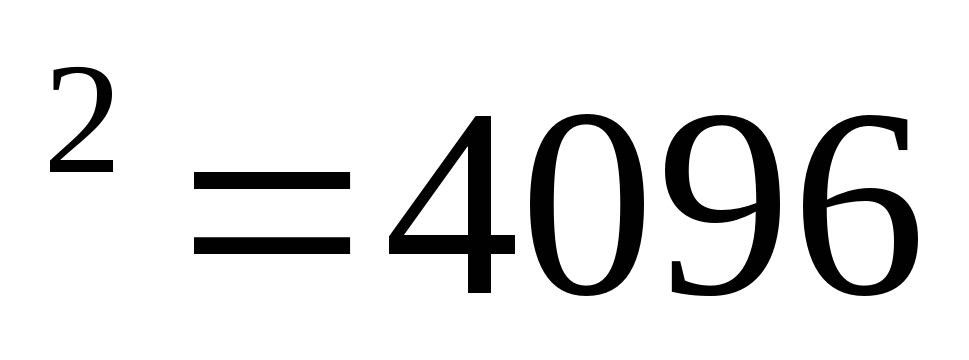

а) 4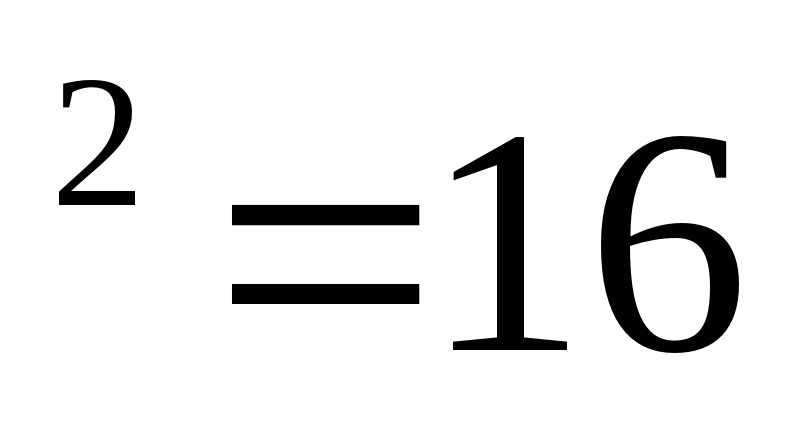; шесть пишем, один запоминаем;

б) (6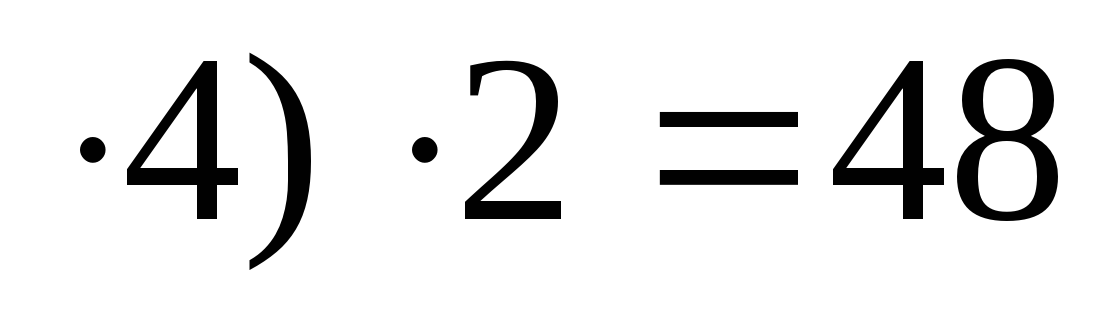; 48 + 1 = 49; девять пишем, четыре запоминаем;

в) 6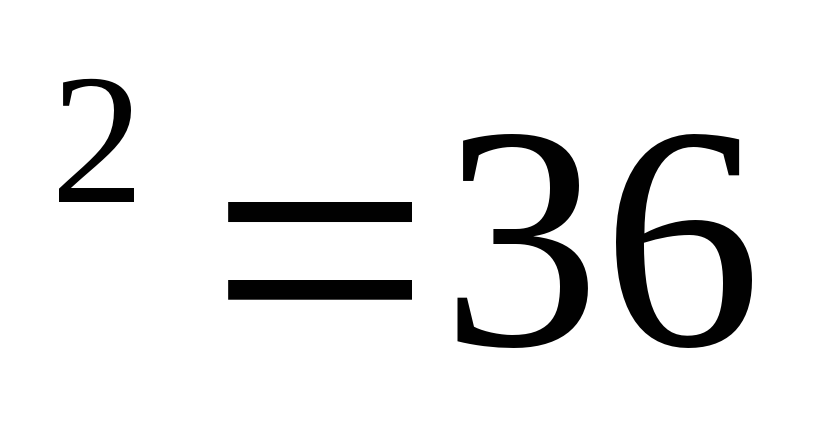; 36 + 4 = 40.

3. Возведение в квадрат двузначных чисел, оканчивающихся на 5.

(10a + 5)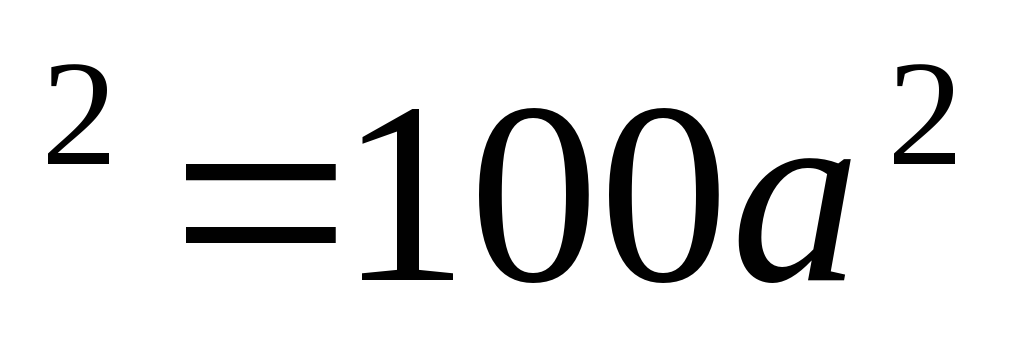+ 100a + 25 = 100a (a+1) + 25,

где a – цифра десятков, 25 – две последние цифры полученного числа:

95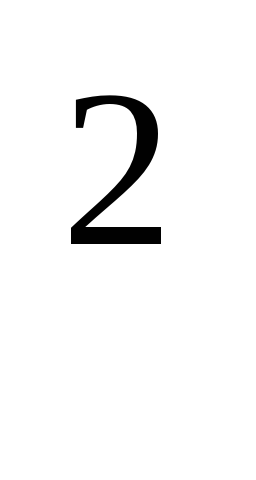= 9025 (9 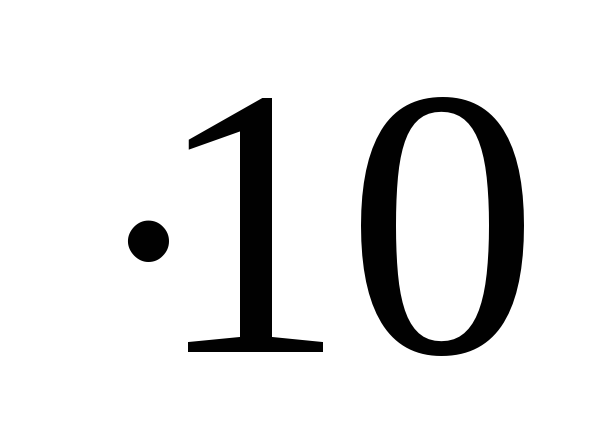= 90 и приписываем 25), т.е.

Для возведения в квадрат числа, запись которого оканчивается цифрой 5, необходимо число десятков умножить на число, увеличенное на единицу, к полученному произведению приписать справа 25.

Этот метод можно использовать для возведения в квадрат трёхзначных чисел, оканчивающихся на 5.

Например:

405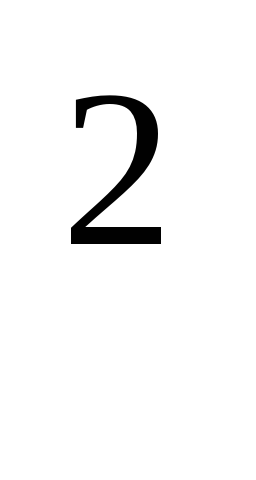= 164025 (40 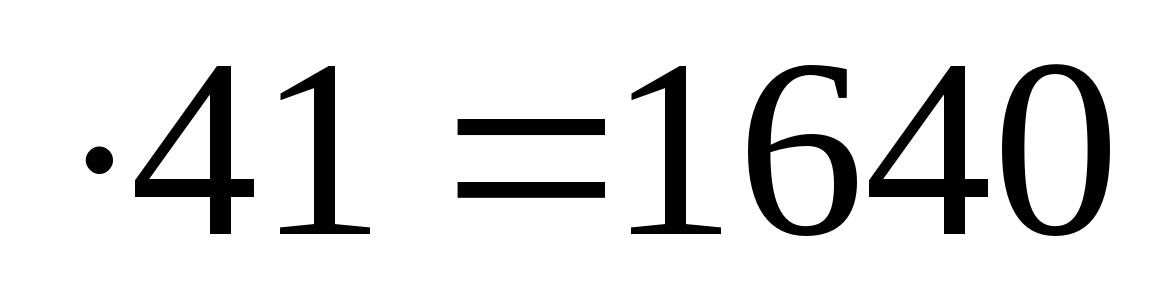и приписываем 25);

165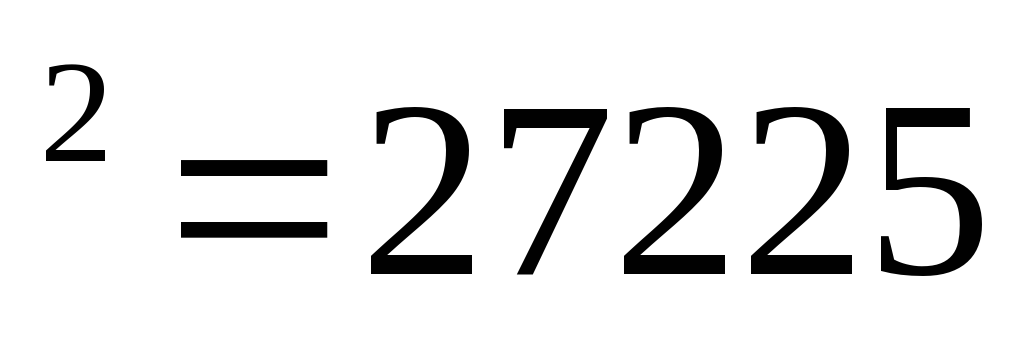 (16 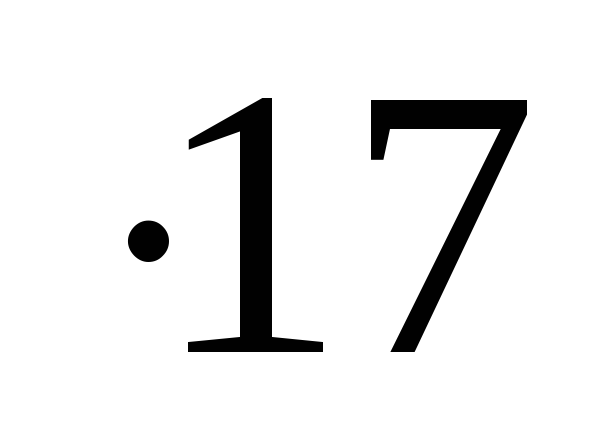- можно применить метод Ферроля).

Все эти правила можно применять при возведении в квадрат десятичных дробей.

4. Применение формулы произведения суммы двух чисел на их разность :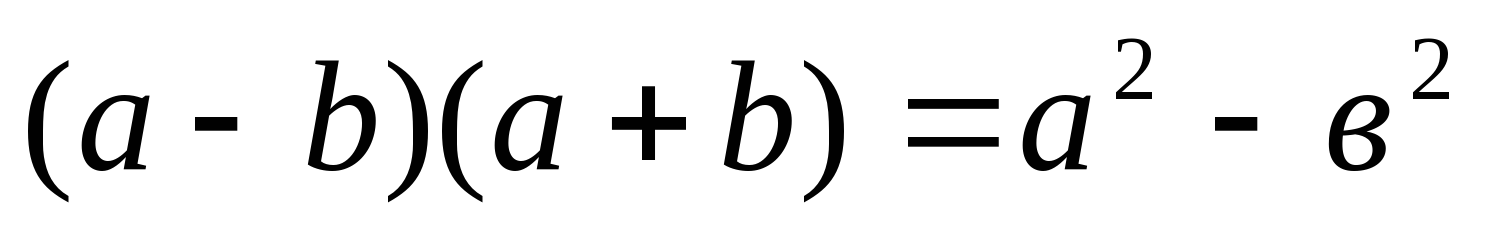

78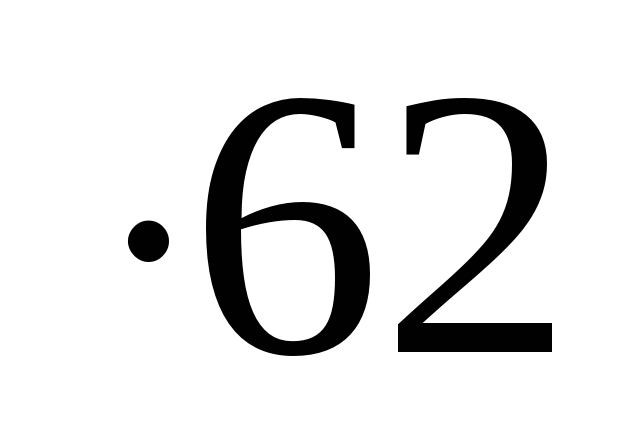= (70+8) (70-8) = 4900 – 64 = 4836;

8,3 ,7 = (8+0,3) (8-0,3) = 64 – 0,09 = 63,91.

5. Применение формулы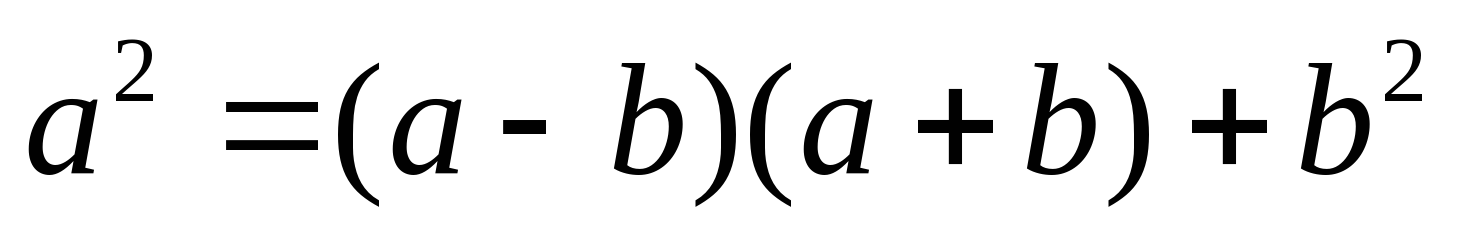

Пример 1:

Возведём в квадрат :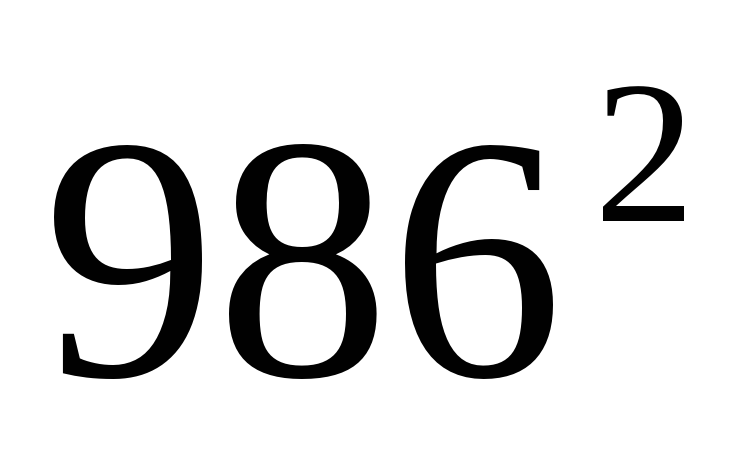

Заметим, что 986 + 14 = 1000. Пусть тогда a = 986, b = 14.

a + b = 1000, a – b = 972. Применяя формулу, получаем:

986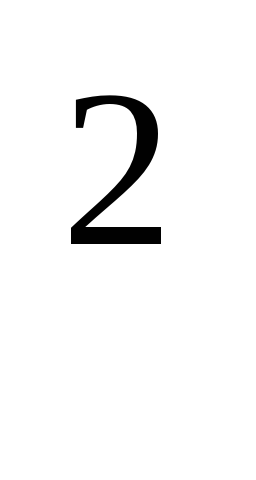= 1000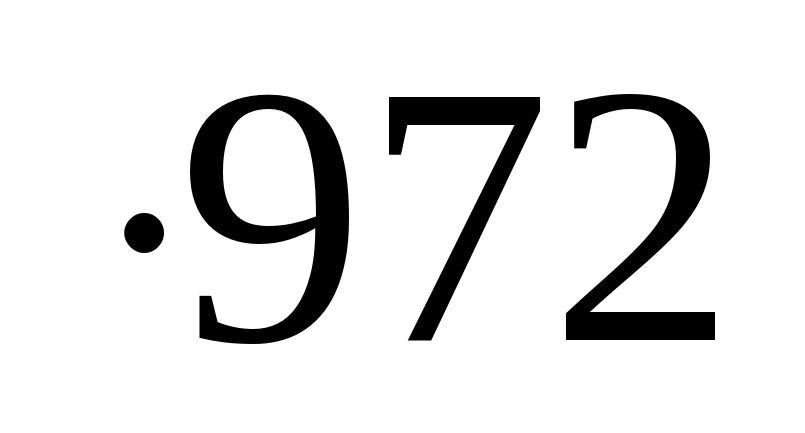+196 = 972196.

Пример 2:

Вычислим 488: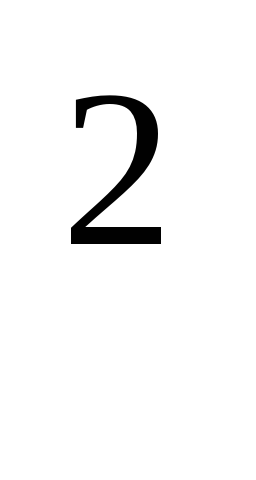

488 + 12 = 500; a = 488, b = 12; a + b = 500, a – b =476.

488= 500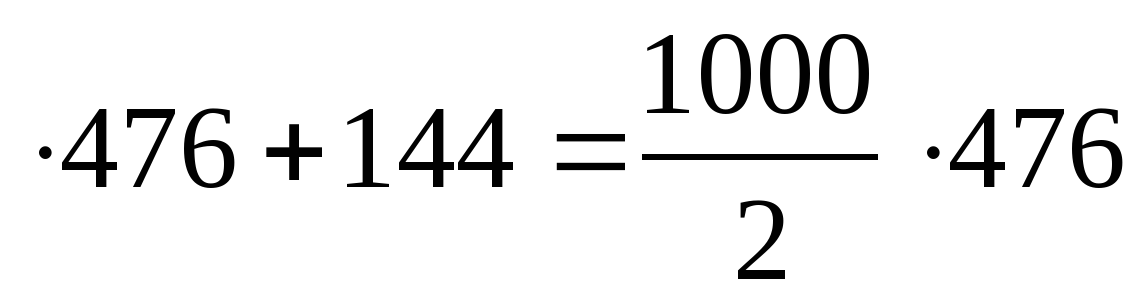+144 = 238000 + 144 = 238144.

6. Умножение чисел, у которых число десятков одинаковое, а сумма единиц равна 10.

Этот способ основан на тождестве: (10a + b) (10a + c) = 100a (a +1) + bc, где b + c =10

Например:

1) 12 · 18 = 216

• число десятков умножаем на число, которое больше на единицу, 1· 2 = 2;

• перемножаем единицы этих чисел и справа дописываем к первому результату 8 · 2 = 16.

2) 46= 2024

• 4;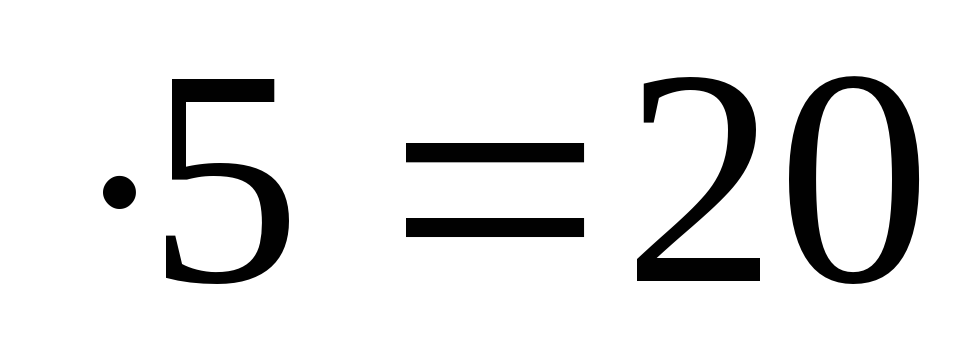

• 6.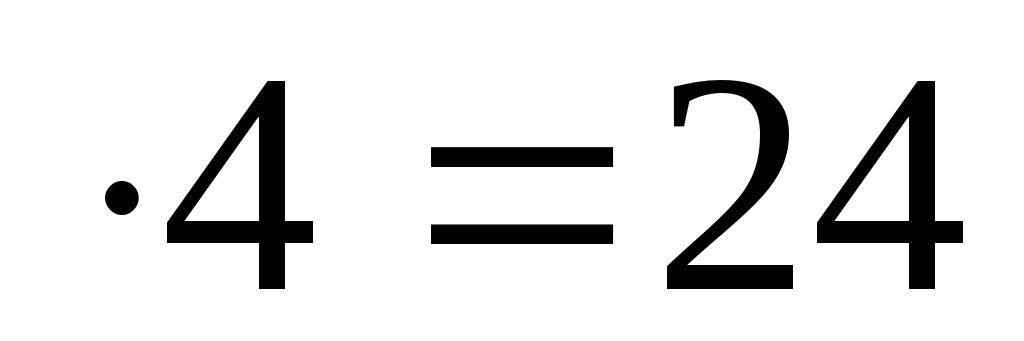

3) 317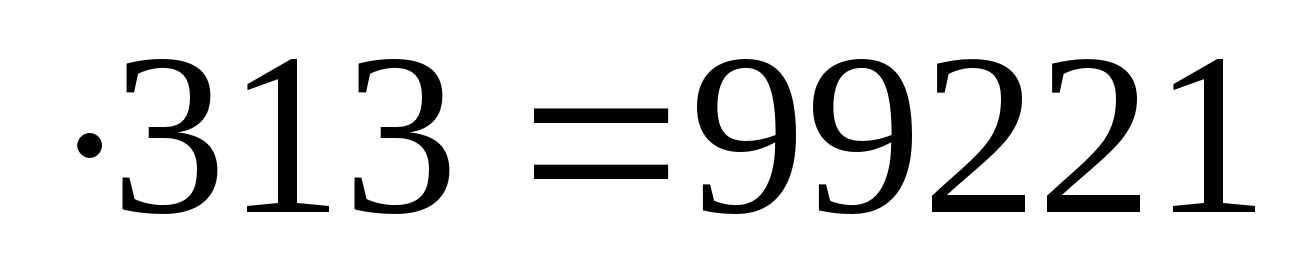

• 31(можно применить метод Ферроля);

• 7.

7. Умножение чисел на 11.

Записать последнюю цифру числа, затем последовательно, справа налево записывать суммы соседних двух цифр множимого и, наконец, первую цифру множимого.

Например:

1. 43 · 11 = 473

• пишем 3;

• 4 + 3 = 7, пишем 7;

• пишем 4.

2. 135 · 11= 1485.

• пишем 5;

• 3 + 5 = 8;

• пишем 14.

Если одна из сумм соседних цифр окажется больше 9, то в этом разряде записывают цифру единиц полученной суммы, а в следующем прибавляют 1.

Например:

1. 57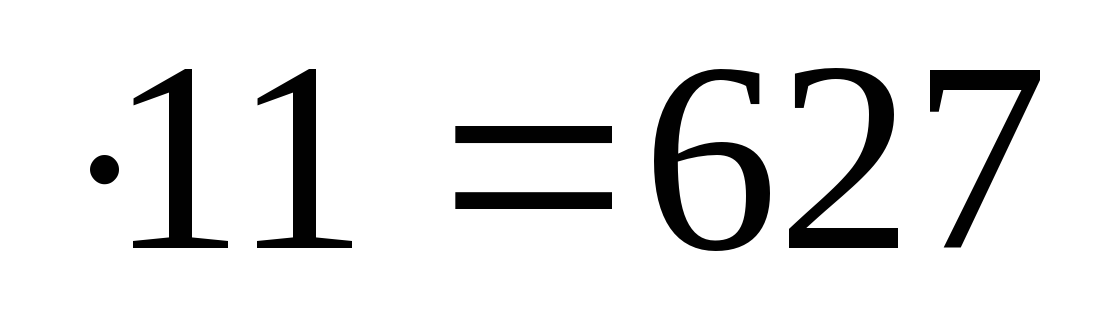

1) пишем 7,

2) 5 + 7 = 12, пишем 2 и запоминаем 1,

3) 5 + 1 = 6.

2. 389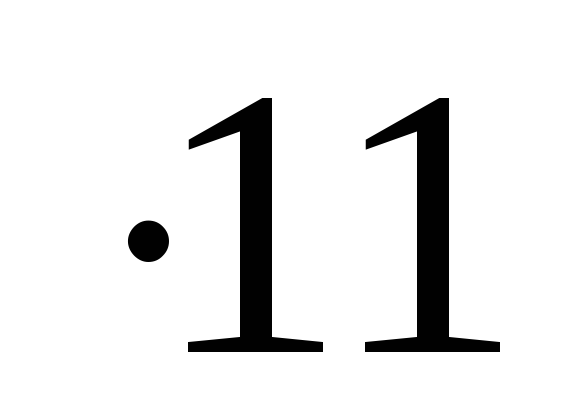= 4279

1) пишем 9,

2) 8 + 9 = 17, пишем 7 и запоминаем 1,

3) 3 + 8 = 11, 11 + 1 = 12, пишем 2, запоминаем 1,

4) 3 + 1 = 4.

8. Умножение на числа вида 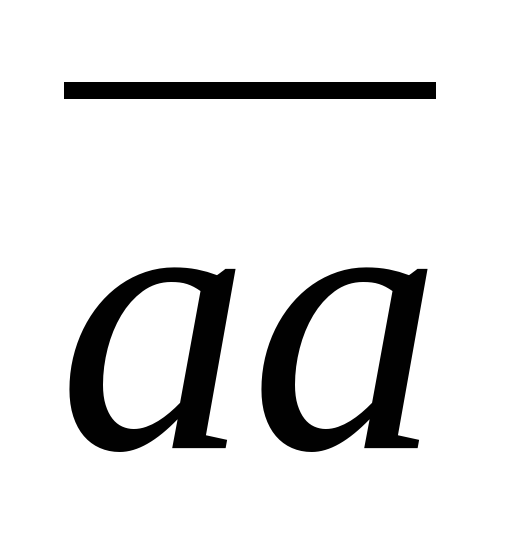: умножить данное число на a, потом на 11.

Например:

235