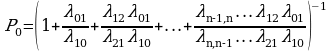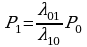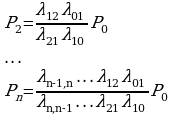Понятие системы массового обслуживания

Понятие системы массового обслуживания связано с явлением ожидания. Обычно очереди наблюдаются у билетных касс, в кафетериях, на автобусных остановках. Для образования очереди необходимо, чтобы клиенты прибывали к такому обслуживающему устройству, у которого им, возможно, придется ожидать, как, например, у кабинета врача, чтобы попасть на прием в порядке записи. Так, телеграммы классифицируются по срочности доставки, и, в свою очередь, обычным телеграммам дается преимущество перед срочными письмами.

Предмет теории массового обслуживания — построение математических моделей, связывающих заданные условия работы СМО (число каналов, их производительность, правила работы, характер потока заявок) с интересующими нас характеристиками — показателями эффективности СМО, описывающими, с той или другой точки зрения, ее способность справляться с потоком заявок. В качестве таких показателей (в зависимости от обстановки и целей исследования) могут применяться разные величины, например: среднее число заявок, обслуживаемых СМО в единицу времени; среднее число занятых каналов; среднее число заявок в очереди и среднее время ожидания обслуживания; вероятность того, что число заявок в очереди превысит какое-то значение, и т. д. Как своеобразные СМО могут рассматриваться: ЭВМ, системы сбора и обработки информации, автоматизированные производственные цеха, поточные линии, транспортные системы, системы ПВО и т.п.

В теории систем массового обслуживания (в дальнейшем CMО) обслуживаемый объект называют требованием. В общем случае под требованием обычно понимают запрос на удовлетворение некоторой потребности, например, разговор с абонентом, посадка самолета, покупка билета, получение материалов на складе.

Средства, обслуживающие требования, называются обслуживающими устройствами или каналами обслуживания. Например, к ним относятся каналы телефонной связи, посадочные полосы, мастера-ремонтники, билетные кассиры, погрузочно-разгрузочные точки на базах и складах.

Всякая СМО предназначена для обслуживания какого-то потока заявок (или «требований»), поступающих в какие-то случайные моменты времени. Обслуживание заявки продолжается какое-то, вообще говоря, случайное время, после чего канал освобождается и готов к приему следующей заявки. Случайный характер потока заявок и времен обслуживания приводит к тому, что в какие-то периоды времени на входе СМО скапливается излишне большое число заявок (они либо становятся в очередь, либо покидают СМО необслуженными); в другие же периоды СМО будет работать с недогрузкой или вообще простаивать.

В СМО происходит какой-то случайный процесс с дискретными состояниями и непрерывным временем; состояние СМО меняется скачком в моменты появления каких-то событий (или прихода новой заявки, или окончания обслуживания, или момента, когда заявка, которой надоело ждать, покидает очередь). Чтобы дать рекомендации по рациональной организации этого процесса и предъявить разумные требования к СМО, необходимо изучить случайный процесс, описать его математически. Этим и занимается теория массового обслуживания.

Основной задачей теории СМО является изучение режима функционирования обслуживающей системы и исследование явлений, возникающих в процессе обслуживания. Так, одной из характеристик обслуживающей системы является время пребывания требования в очереди. Очевидно, что это время можно сократить за счет увеличения количества обслуживающих устройств. Однако каждое дополнительное устройство требует определенных материальных затрат, при этом увеличивается время бездействия обслуживающего устройства из-за отсутствия требований на обслуживание, что также является негативным явлением. Следовательно, в теории СМО возникают задачи оптимизации: каким образом достичь определенного уровня обслуживания (максимального сокращения очереди или потерь требований) при минимальных затратах, связанных с простоем обслуживающих устройств.

Входящий поток требований

Процесс поступления в систему массового обслуживания требований является вероятностным. Это поток однородных или неоднородных событий, которые поступают через случайные промежутки времени. Поток характеризуется частотой появления событий или средним число событий, которые поступают в СМО в единицу времени. Если события следуют одно за другим через определенные равные промежутки времени - поток событий называется регулярным (к примеру, поток изделий на конвейере сборочного цеха, если он движется с постоянной скоростью) Если вероятностные характеристики потока событий не зависят от времени, то поток событий является стационарным. Поток событий называется потоком без последействия, если для любых двух непересекающихся участков времени число событий, попадающих на один из них, не зависит от числа событий, попадающих на другие. Если вероятность попадания на малый (элементарный) участок времени двух и более событий мала по сравнению с вероятностью попадания одного события, то поток событий является ординарным. То есть, поток событий ординарен, если события появляются в нем не группами, а поодиночке. Если поток событий (требований) одновременно стационарен, одинарен и не имеет последействия- то поток событий называется простейшим.

Структура системы

Для задания структуры СМО необходимо перечислить все приборы, имеющиеся в системе, и указать, заявки каких типов может обслуживать каждый прибор. При этом отдельный прибор может обслуживать заявки нескольких типов и, наоборот, заявки одного типа могут обслуживаться несколькими приборами.

В дальнейшем мы в основном ограничимся случаем, когда в СМО имеется один или несколько одинаковых приборов и каждая заявка может обслуживаться на любом из них. Системы такого типа называются одноканальными (в случае одного прибора) или многоканальными полнодоступными (при нескольких приборах). Кроме того, будем предполагать, что после окончания обслуживания заявка покидает систему и больше в нее не возвращается, т.е. система является однофазной.

Представление о методах расчета многофазных СМО, в которых заявка должна последовательно обслужиться на нескольких приборах (пройти несколько фаз обслуживания), дают сети массового обслуживания.

В этих темах обслуживания могут быть предусмотрены накопители различной емкости, или места для ожидания, которые предоставляют возможность заявкам, заставшим в момент своего поступления в систему все приборы занятыми, ожидать начала обслуживания.

Времена обслуживания заявок

Времена обслуживания заявок на приборах также представляет собой сложный объект для формализованного описания.

Вообще говоря, наряду с непрогнозируемыми случайными флуктуациями могут существовать систематические изменения времен обслуживания заявок с течением календарного времени, зависимость времен обслуживания от процессов поступления и обслуживания других заявок и т.д.

Однако обычно предполагается, что времена обслуживания всех заявок суть независимые между собой и от всех протекающих в системе процессов одинаково распределенные случайные величины. В этом случае говорят о рекуррентном обслуживании. Тогда время обслуживания любой заявки характеризуется лишь одной функцией распределения.

Если в СМО поступают заявки нескольких типов, то распределение времени обслуживания может зависеть от типа заявки.

Дисциплина обслуживания

Как уже говорилось, дисциплина обслуживания заключается в правиле постановки заявок в очередь и порядке их выбора из очереди на обслуживание, распределении приборов между заявками, в многофазных системах и между фазами обслуживания.

В основном мы будем предполагать, что в системе реализована естественная дисциплина обслуживания заявок в порядке поступления. В многоканальных системах, в которых организуется общая очередь ко всем приборам, находящаяся в очереди первой заявка поступает на любой освободившийся прибор.

Тем не менее, в СМО могут быть использованы и более сложные дисциплины обслуживания. Простейшими примерами таких дисциплин является: инверсионный порядок обслуживания, при котором первой обслуживается заявка, поступившая в систему последней, случайный выбор на обслуживание, когда при наличии в системе п заявок на прибор с вероятностью 1/n поступает любая из них, и дисциплина равномерного разделения прибора, при которой каждая п находящихся в системе заявок обслуживается с одинаковой скоростью 1/n.

Процесс гибели и размножения

В теории массового обслуживания широкое распространение имеет специальный класс случайных процессов — так называемый процесс размножения и гибели. Название этого процесса связано с рядом задач, которые описывают динамику биологических популяций. Граф состояния процесса размножения и гибели имеет вид:

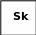
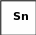
λn-1,n

λk,k+1

λk-1,k

λ23

λ12

λ01

S₁

S₀

λn,n-1

λ10

λk,k-1

λk+1, λ

λ32

λ21

Рассмотрим упорядоченное множество состояний системы S₀, S₁, S₂, …, S_k. Переходы могут осуществляться из любого состояния только в состояние с соседним номером, т.е. из состояния S_k возможны только переходы в состояние S_k-1 или S_k+1. Будем полагать, что все потоки событий простейшие, с соответствующими интенсивностями λ_k,k+1 или λ _k+1,_k. По графу состояний составим и решим алгебраические уравнения для предельных вероятностей. В соответствии с правилами составления таких уравнений получим:

S₀: λ₀₁ P₀ = λ₁₀ P₁

S₁: (λ₁₂ + λ₁₀ )P₁ = λ₀₁ P₀+ λ₂₁ P₂ = λ₁₂ P₁ = λ₂₁ P₂

Аналогично записываются уравнения для предельных вероятностей других состояний, получим следующую систему уравнений:

λ₀₁ P₀ = λ₁₀ P₁

λ₁₂ P₁ = λ₂₁ P₂

…

λ_k-1,k P_k-1 = λ_k,k+1 P_k

λ_n-1,n P_n-1 = λ_n,n+1 P_n

К которой добавляется нормированное условие:

P₀+ P₁+ P₂+…+ P_n=1

Решая данные системы получим:

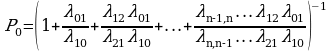
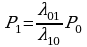
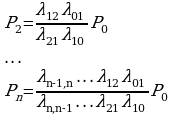
В этой формуле числители коэффициентов при P₀ представляются произведением всех интенсивностей, стоящих у стоящих у стрелок слева направо до данного состояния S_k(k=1,2,…,n), а знаменатели произведения всех интенсивностей, стоящих у стрелок , ведущих справа налево до состояния S_k.

Классификация систем массового обслуживания

Системы массового обслуживания классифицируют по разным признакам. К таким признакам относятся условия ожидания требования начала обслуживания. В соответствии с этим признаком системы подразделяются на следующие виды:

- системы массового обслуживания с потерями (отказами);

- системы массового обслуживания с ожиданием;

- системы массового обслуживания с ограниченной длиной очереди;

- системы массового обслуживания с ограниченным временем ожидания.

Системы массового обслуживания, у которых требования, поступающие в момент, когда все приборы обслуживания заняты, получают отказ и теряются, называются системами с потерями или отказами.

Системы массового обслуживания, у которых возможно появление как угодно длинной очереди требований к обслуживающему устройству, называются системами с ожиданием.

В таких системах заявка, поступившая в момент, когда все каналы заняты, становится в очередь и ожидает, пока не освободится один из каналов. Когда канал освобождается, одна из заявок, стоящих в очереди, принимается к обслуживанию.

Обслуживание (дисциплина очереди) в системе с ожиданием может быть упорядоченным (заявки обслуживаются в порядке поступления), неупорядоченным (заявки обслуживаются в случайном порядке) или стековым (первой из очереди выбирается последняя заявка). Кроме того, в некоторых СМО применяется так называемое обслуживание с приоритетом, когда некоторые заявки обслуживаются в первую очередь, предпочтительно перед другими. Здесь также различаются системы со статическими и динамическими приоритетами (в последнем случае приоритет может, например, увеличиваться с длительностью ожидания заявки).

Системы с очередью делятся на системы с неограниченным и с ограниченным ожиданием.

Системы массового обслуживания, допускающие очередь, но с ограниченным сроком пребывания каждого требования в ней, называются системами с ограниченным временем ожидания.

В системах с неограниченным ожиданием каждая заявка, поступившая в момент, когда нет свободных каналов, становится в очередь и «терпеливо» ждет освобождения канала, который примет ее к обслуживанию. Любая заявка, поступившая в СМО, рано или поздно будет обслужена.

Системы массового обслуживания, допускающие очередь, но с ограниченным числом мест в ней, называются системами с ограниченной длиной очереди.

В системах с ограниченным ожиданием на пребывание заявки в очереди накладываются те или другие ограничения. Эти ограничения могут касаться как длины очереди (числа заявок, одновременно находящихся в очереди — система с ограниченной длиной очереди), так и времени пребывания заявки в очереди (после какого-то срока пребывания в очереди заявка покидает очередь и уходит — система с ограниченным временем ожидания), либо общего времени пребывания заявки в СМО и т. д.

В зависимости от типа СМО при оценке ее эффективности могут применяться те или другие величины (показатели эффективности). Например, для СМО с отказами одной из важнейших характеристик ее продуктивности является так называемая абсолютная пропускная способность — среднее число заявок, которое может обслужить система за единицу времени.

Наряду с абсолютной часто рассматривается относительная пропускная способность СМО — средняя доля поступивших заявок, обслуживаемая системой (отношение среднего числа заявок, обслуживаемых системой в единицу времени, к среднему числу поступающих за это время заявок).

Помимо абсолютной и относительной пропускной способностей при анализе СМО с отказами нас могут, в зависимости от задачи исследования, интересовать и другие характеристики, например:

- среднее число занятых каналов;

- среднее относительное время простоя системы в целом и отдельного канала и т. д.

СМО с ожиданием имеют несколько другие характеристики. Очевидно, для СМО с неограниченным ожиданием как абсолютная, так и относительная пропускная способность теряют смысл, так как каждая поступившая заявка рано или поздно будет обслужена. Зато для такой СМО весьма важными характеристиками являются:

- среднее число заявок в очереди;

- среднее число заявок в системе (в очереди и под обслуживанием);

- среднее время ожидания заявки в очереди;

- среднее время пребывания заявки в системе (в очереди и под обслуживанием);

и другие характеристики ожидания.

Для СМО с ограниченным ожиданием интерес представляют обе группы характеристик: как абсолютная и относительная пропускная способности, так и характеристики ожидания.

Для анализа процесса, протекающего в СМО, существенно знать основные параметры системы: число каналов n, интенсивность потока заявок λ, производительность каждого канала (среднее число заявок μ, обслуживаемое каналом в единицу времени), условия образования.[2]

По числу каналов или приборов системы делятся на одноканальные и многоканальные.

Кроме этих признаков, СМО делятся на два класса: «открытые» и «замкнутые». В открытой СМО характеристики потока заявок не зависят от того, в каком состоянии сама СМО (сколько каналов занято). В замкнутой СМО — зависят. Например, если один рабочий обслуживает группу станков, время от времени требующих наладки, то интенсивность потока «требований» со стороны станков зависит от того, сколько их уже неисправно и ждет наладки. Это — пример замкнутой СMO.

В зависимости от типа СМО при оценке её эффективности могут применяться те или иные величины (показатели эффективности). Например, для СМО с отказами одной из важнейших характеристик её продуктивности является так называемая абсолютная пропускная способность – среднее число заявок, которое может обслужить система за единицу времени. Наряду с абсолютной, часто рассматривается относительная пропускная способность – средняя доля поступивших заявок, обслуживаемая системой (отношение среднего числа обслуживаемых в единицу времени заявок к среднему числу поступающих заявок за это время). Помимо этого при анализе СМО с отказами могут интересовать ещё среднее число занятых каналов, среднее относительное время простоя системы в целом и отдельного канала и т.д.

Характеристики СМО с ожиданиями. Для СМО с неограниченным ожиданием абсолютные и относительные пропускные способности теряют смысл. Зато важными являются: среднее число заявок в очереди, среднее число заявок в системе (в очереди и под обслуживанием), среднее время ожидания заявки в очереди, среднее время пребывания заявки в системе и другие. Для СМО с ограниченным ожиданием интерес представляют обе группы характеристик.

Для анализа процесса, протекающего в СМО, существенно знать основные параметры системы: число каналов n, интенсивность потока заявок λ, производительность каждого канала (среднее число заявок μ, обслуживаемых непрерывно занятым каналом в единицу времени), условия образования очереди (ограничения, если они есть).

Условимся все потоки событий, переводящие СМО из состояния в состояние, считать пуассоновскими.

Показатели эффективности СМО

К показателям эффективности СМО относят:

- распределение вероятности для числа требований n в системе;

- среднее число требований в очереди или в системе;

- распределение времени ожидания в очереди или времени пребывания требования в системе;

- среднее и дисперсия времени ожидания;

- средняя длительность интервала занятости системы;

- среднее число обслуживаемых за единицу времени требований;

- распределение вероятности для числа занятых каналов системы;

- стоимости: каналов обслуживания, потерь от несвоевременного обслуживания (очередей), стоимости диспетчеризации (управление, перенаправление) потоков требований и др.

Все показатели качества обслуживания систем можно условно разделить на три вида: вероятностные, моментные, экономические, которые тесно связаны между собой. Из вероятностных характеристик широко применяются такие как:

P(k = n), или, сокращенно Р(n) - вероятность того, что в системе находится n требований;

P(knmax) - вероятность потери текущего требования, и др.

В установившемся состоянии работы СМО, если такое существует, выходной поток равняется входному: λвх = λвых = λс. Если, кроме того, входные требования не зависят от выходных (разомкнутая система), то предыдущие уравнения приводятся к виду:

интенсивность потока требований × средняя длительность пребывания требования в системе = среднее число требований в очереди.

Очевидно, что чем меньшее значение таких показателей, как n, k, тем выше эффективность системы с точки зрения источника требований (клиента). Однако, уменьшение значений этих показателей связано с повышением экономических расходов исполнителя.

В состав обобщенного критерия эффективности СМО включают стоимость ожидания требований в очереди и стоимость простоя каналов. Первая составляющая - потери клиента, вторая – расходы исполнителя. Будет ли исполнитель учитывать первую составляющую? - В условиях конкуренции и, если он планирует бизнес надолго, - будет обязательно.