| Организационная структура урока |
| Этап урока | Содержание деятельности учителя | Содержание деятельности обучающегося
(осуществляемые действия) | Формируемые способы
деятельности |
| I. Организационный момент | Приветствие. Проверка готовности обучающихся к уроку. Создание в классе атмосферы психологического комфорта.
| Настраиваются на учебную деятельность. Концентрируют внимание на работе на уроке.
| Формирование навыков самоорганизации |
| II. Актуализация опорных знаний и жизненного опыта. Постановка учебной задачи | Предлагает обучающимся рассказать, что им известно о понятии «последовательность». В 9 классе на уроках алгебры мы уже встречались с понятием числовой последовательности. Рассматривали свойства некоторых последовательностей, способы их задания. Арифметическая и геометрическая прогрессии нами были изучены более подробно. Мы познакомились с формулами n-го члена прогрессии, суммы n первых членов прогрессии. Настало время вспомнить и обобщить изученный материал, систематизировать его и применить к более сложным понятиям.
| Отвечают на вопросы учителя. – Я знаю… – Я помню… – Нам рассказывали… – Я выполнял… Осознают важность решения поставленной учебной задачи | Развитие навыков целеполагания |
| III. Сообщение темы. Постановка цели и задач урока | На доске записанонесколько последовательностей чисел, ученики словесно формулирубт название каждоц из нихСообщает тему урока. Организует совместное с учащимися формулирование цели и задач урока.
| | Пример последовательности | Название последовательности (формулируют ученики) | | 1, 2, 3, 4, 5, … | Последовательность натуральных чисел | | 2, 4, 6, 8, 10, … | Последовательность четных чисел | | 0,3; 0,33; 0,333; … | Последовательность десятичных приближений дроби 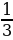 | | 19, 38, 57, 76, 95 | Последовательность двузначных чисел, кратных 19 | | –1, –2, –3, –4, –5, … | Последовательность отрицательных целых чисел |
Записывают в тетрадь тему урока. Участвуют в формулировании целей и задач урока:
| Умение принимать и сохранять учебную задачу |
| IV. Мотивирование к учебной деятельности | Способствует обсуждению мотивационных вопросов. – Есть ли у меня желание узнавать что-то новое? – Что меня заинтересовало в теме урока? – При каких условиях урок будет для меня полезным? – Какова моя цель на данный урок? | Отвечают на мотивационные вопросы. Создают условия для успешной учебной деятельности. | Умение выражать свои мысли, демонстрировать самомотивацию |
| V. Создание ситуации затруднения. Работа над темой урока | Организует обсуждение проблемного вопроса: – С какими объектами удобней работать, если они пронумерованы? Будем рассуждать более строго. Пронумеруем все члены последовательности по порядку: 1, 2, 3, …, n, …
Существует некий закон (некое правило), по которому каждому из этих натуральных чисел ставится в соответствие определенное число (соответствующий член последовательности). В примере (2) это соответствие выглядит так: | Член посл | 2 | 4 | 6 | 8 | | Номер посл | 1 | 2 | 3 | 4 |
В общем виде указанное соответствие можно изобразить так: У1 у2 у3 у4 у5….уn
1 2 3 4 5 … n …
Число есть n-ый член последовательности. Всю последовательность обычно обозначают (yn) или (an) . Определение числовой последовательности можно дать – как функции, заданной на множестве натуральных чисел.
Последовательности можно задавать словесно, как в начале урока, а можно с помощью формул, например эту можно задать У п = 2*n
Например, формула 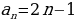 задает последовательность натуральных нечетных чисел: задает последовательность натуральных нечетных чисел: 1, 3, 5, 7, 9, … . Определение: Функцию у= f(x) где х €N называют последовательностью и обозначают (уn) Свойства последовательности: Последовательность (уn) называется неубывающей, если 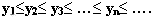 . . Последовательность (уn) называется невозрастающей, если 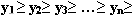 Неубывающие и невозрастающие последовательности объединяют под названием монотонных последовательностей. Последовательность 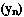 называется ограниченной, если можно указать такие два числа А и В, между которыми лежат все члены последовательности. называется ограниченной, если можно указать такие два числа А и В, между которыми лежат все члены последовательности. 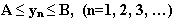
| Принимают участие в обсуждении решения задачи. Осуществляют поисково-исследовательскую деятельность. Работают с разными источниками информации. Анализируют примеры числовых последовательностей. Делают записи в тетради. Задают вопросы учителю. Анализируют информацию. Анализируют предложенное решение задания. Формулируют вопросы учителю для уточнения логики решения задания.
| Умение выражать свои мысли в соответствии с задачей.
Умение анализировать информацию
|
| VI. Закрепление изученного материала | Организует решение заданий по вопросам
| Приводят примеры неубывающей (возрастающей), ограниченной последовательностей | Умение осуществлять актуализацию полученных на уроке знаний и умений |
| VII. Решение заданий | Организует решение заданий по учебнику | Решают задания | Умение осу-ществлять акту-ализацию полу-ченных на уроке знаний и умений |
| VIII. Подведение итогов урока. Рефлексия | Организует подведение итогов урока обучающимися. Способствует размышлению учащихся над вопросами. – Можно ли сказать, что я понимаю, что собой представляет числовая последовательность? – Есть ли у меня желание рассказать о числовых последовательностях своим друзьям? – Доволен ли я своей работой на уроке? – Получил ли я удовольствие от процесса познания нового? | Подводят итоги своей работы на уроке. Проводят самооценку, рефлексию. | Умение отслеживать цель учебной деятельности |
| IХ. Домашнее задание | Помогает учащимся выбрать задания из учебника. Обращает внимание на возможности и способности обучающихся | Выбирают задания, которые будут решать дома. Записывают домашнее задание. | Формирование навыков самоорганизации |







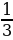
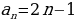 задает последовательность натуральных нечетных чисел:
задает последовательность натуральных нечетных чисел:









