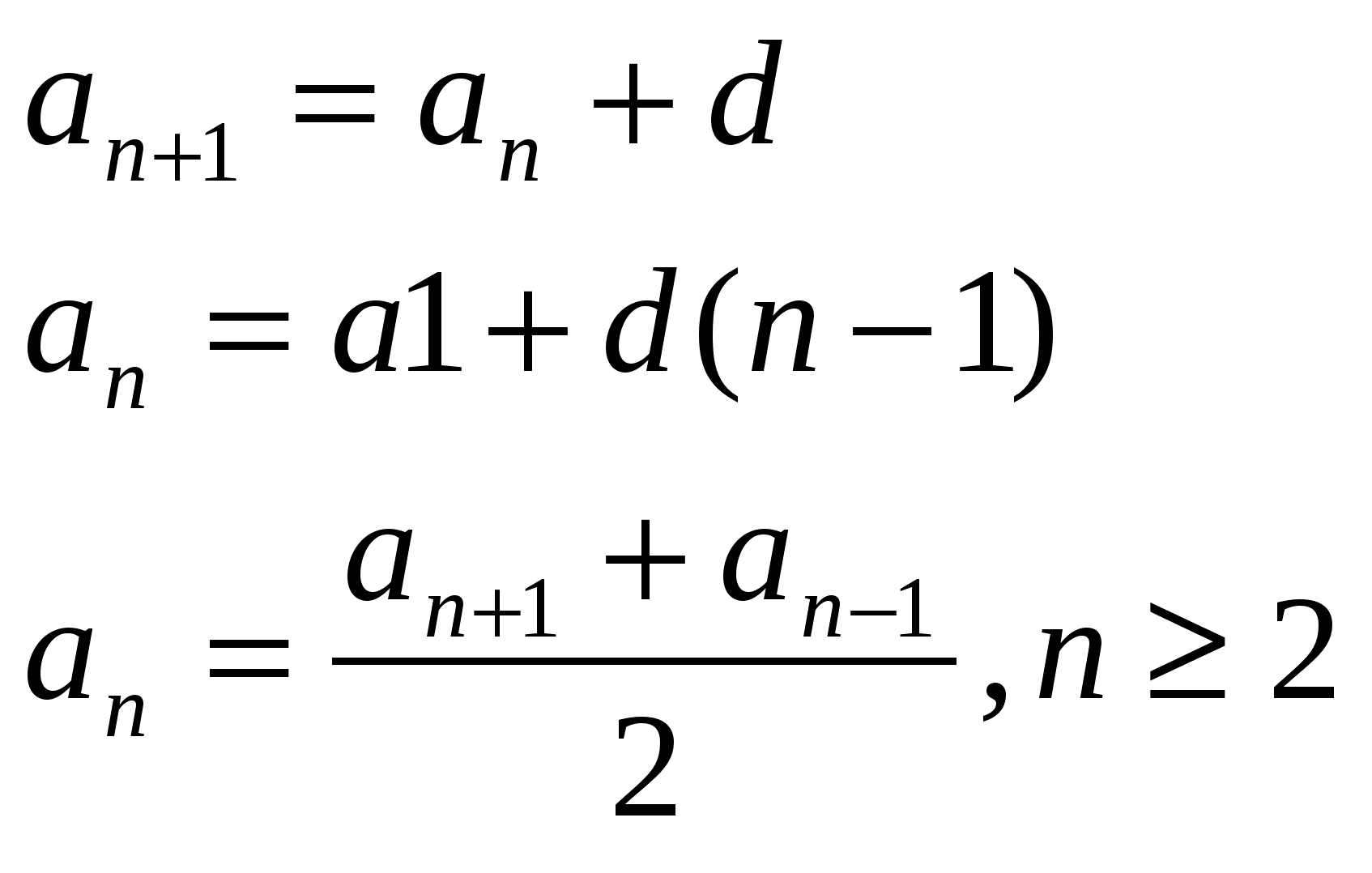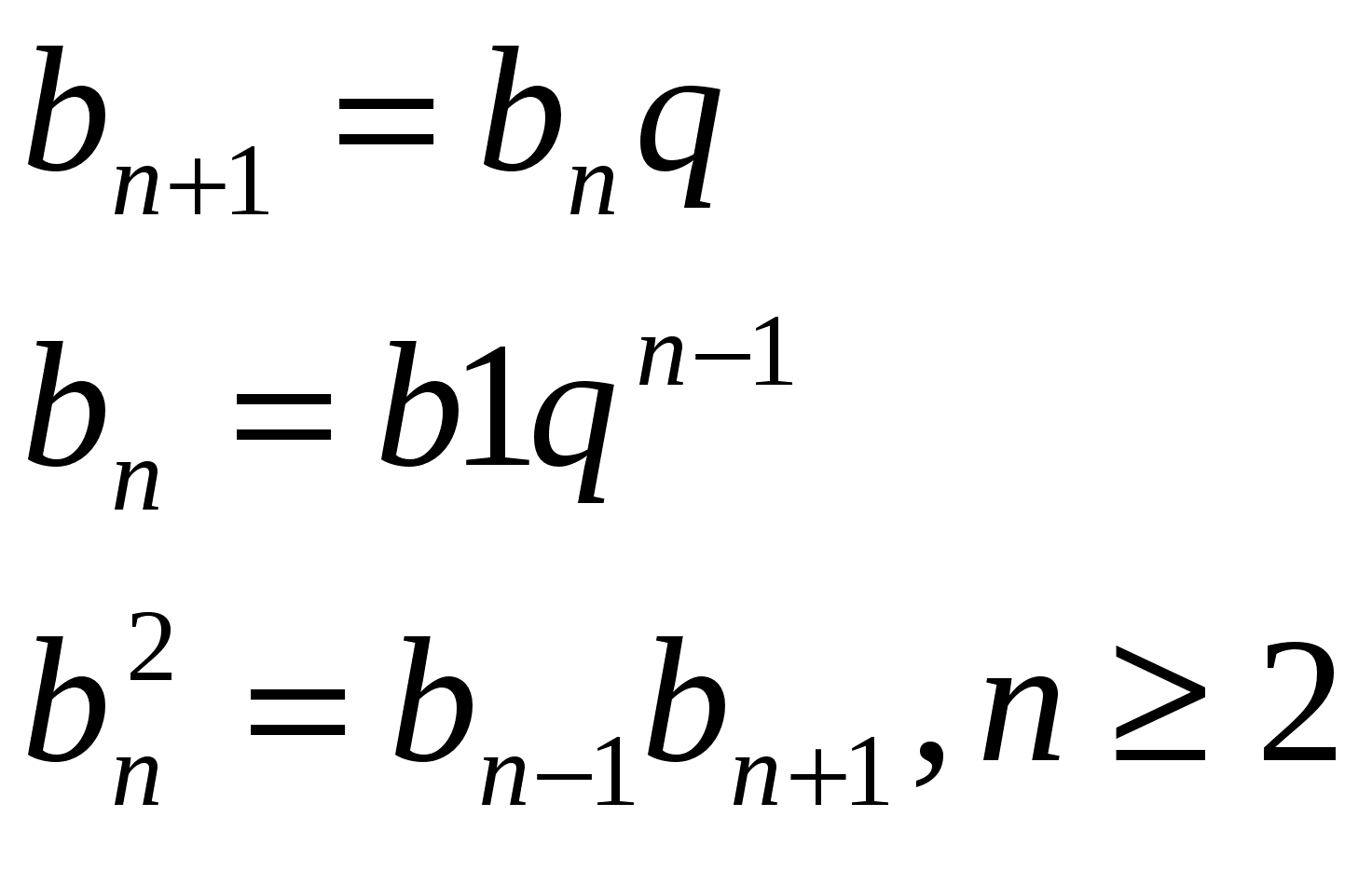Последовательности и прогрессии

Учебно- исследовательская конференция учащихся

«Спектр»

Секция математики

Последовательности и прогрессии в нашей жизни

Исследовательская работа

Выполнил:

Ученик 9 «А» класса

МБОУ «Центр образования №32»

Строганов Никита Сергеевич

Научный руководитель –

учитель математики

МБОУ «Центр образования №32»

Елисеева Ольга Григорьевна

Череповец, 2016 год

Учебно-исследовательская конференция

«Спектр»

Секция математики

Последовательности и прогрессии в нашей жизни

Исследовательская работа

Выполнил:

Ученик 9 «А» класса

Череповец, 2016 год

Оглавление

Введение…………………………………………………3-7

Формулы………………………………………..……….…8

История прогрессий………………………..………….......9

Прогрессии в природе………………………………....10-13

Прогрессии в химии...……...………………………….14-15

Прогрессии в физике…….……………...…………..…16-17

Прогрессии в литературе…….………………………….. 18

Прогрессии в экономике………………………………….19

Интересные факты………………………………..........20-23

Анкетирование…………………………………………….24

Вывод……………...……………………………………….25

Литература………………………………………………....26

Источники………………………………………………….27

Введение

Актуальность:

В 9 классе мы изучаем прогрессии, даем определения, учимся находить по формулам любой член прогрессии, сумму первых членов прогрессии. Найдя ответы на вопросы: имеют ли прогрессии какое-либо практическое применение, как давно люди знают последовательности и как возникло это понятие, мы подтвердим или опровергнем суждение о том, что математика возникла очень давно из практических нужд человека, что она является важной частью общечеловеческой культуры.

Цель:

Установить картину возникновения понятия прогрессии, выявить примеры их применения в нашей жизни и экспериментально доказать присутствии прогрессий в различных природных явлениях.

Задачи:

1.Дать определение прогрессиям.

2.Установить факты широкого применения прогрессии во всех областях науки.

3.Выяснить: когда появилось понятие последовательности, в частности прогрессии.

4.Найти примеры прогрессий в нашей жизни.

5.Выявить интересные факты о прогрессиях.

6. Провести анкетирование на знание применения последовательностей среди учащихся 9-ых классов.

Объект исследования:

Арифметическая и геометрическая прогрессии.

Предмет исследования:

Практическое применение прогрессий.

Гипотеза исследования:

Математика – древняя наука, возникшая из жизненно необходимых нужд человека. Значит, прогрессии тоже имеют определённое практическое значение.

Методы исследования:

1.Анализ справочной литературы и материала из Интернета по заявленной теме;

2.Экспериментальный путь доказательства существования прогрессий в том или ином явлении;

3.Поиск прогрессий в окружающем мире.

Практическая значимость работы состоит в том, что задачи на арифметическую и геометрическую прогрессию часто встречаются на экзаменах по математике

Формулы

Прогрессии бывают двух видов:

1. Арифметическая прогрессия — числовая последовательность, в которой каждое число, начиная со второго, получается из предыдущего добавлением к нему постоянного числа (шага, или разности прогрессии).

2. Геометрическая прогрессия — последовательность чисел, в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число (знаменатель прогрессии).

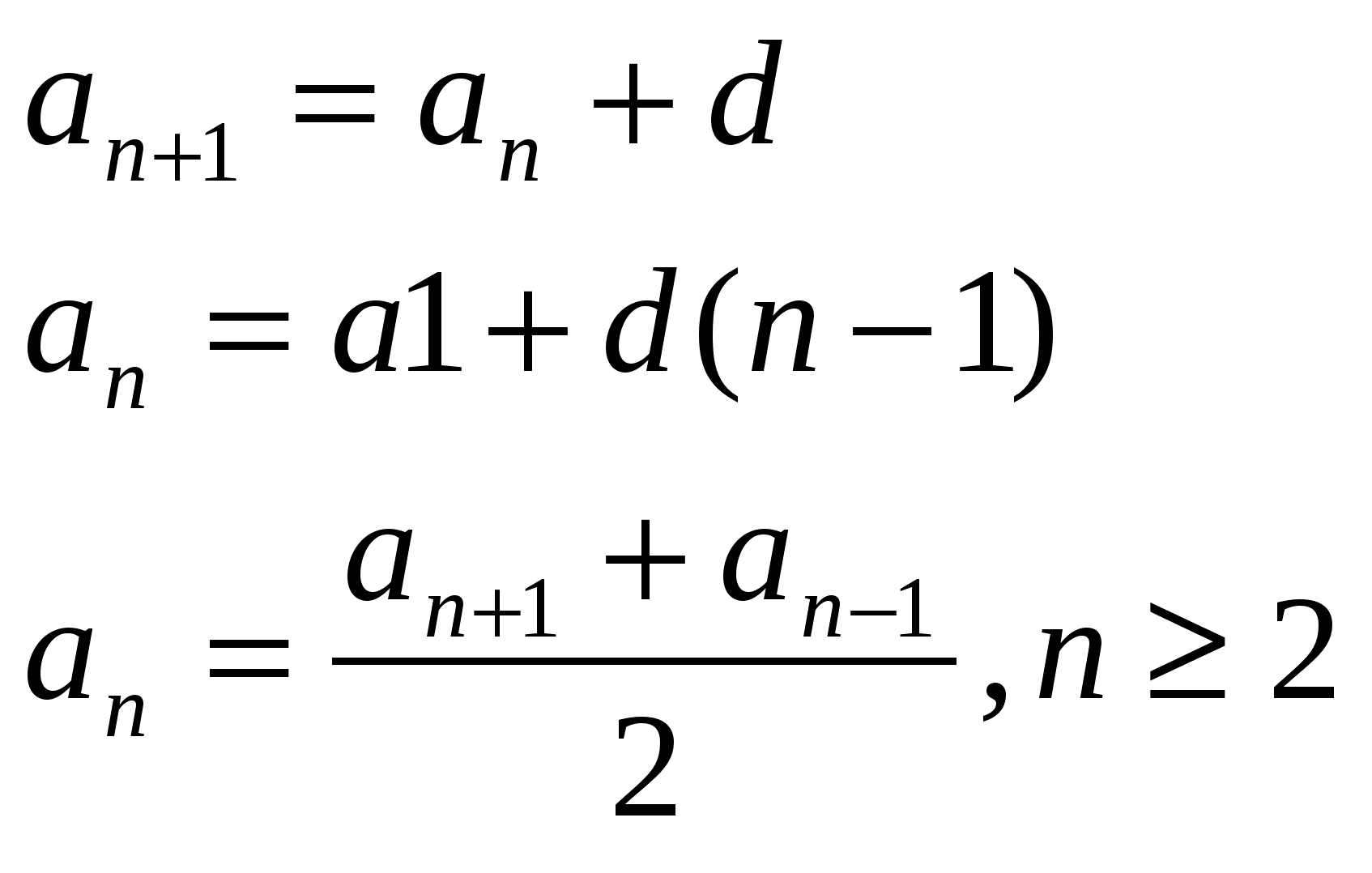
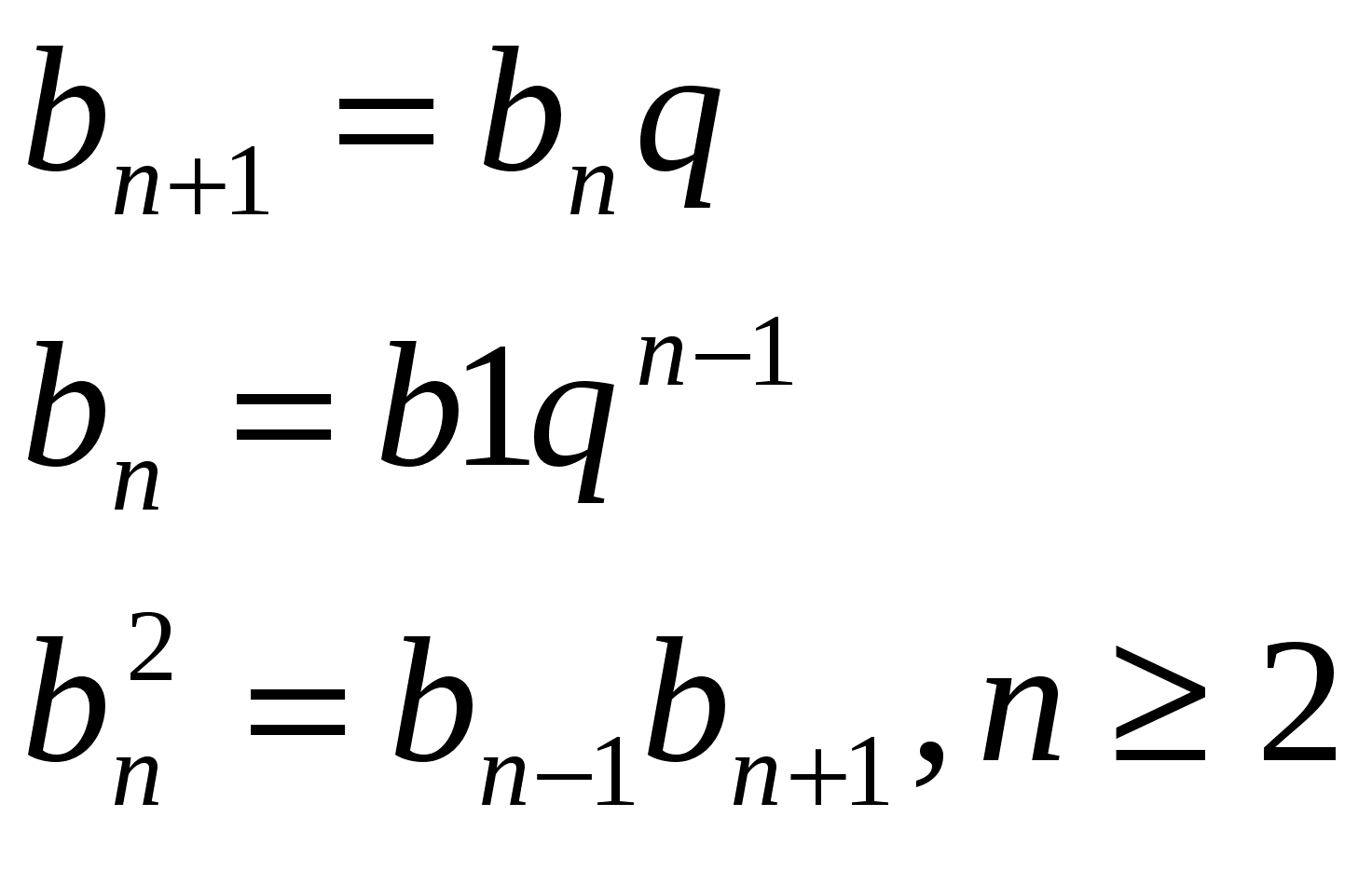
История термина

Термин «прогрессия» был введен римским автором Боэцием в VI веке н.э. и означал «движение вперед». Этим термином в математике прежде называли всякую последовательность чисел, построенную по такому принципу, который позволяет неограниченно продолжать эту последовательность в одном направлении.

Сами по себе прогрессии известны очень давно, поэтому историки не называют конкретного человека, открывшего их.

Прогрессии в природе

Известно что один одуванчик ежегодно приносит около ста семян. Если бы все семена прорастали, мы имели бы в первый год 1 растение, во второй – 100, в третий 100^2 растений, в четвертый – 100^3 и т. д., в девятый – 100^8. Но это число в 70 раз больше, чем имеется квадратных метров на всей суше! Следовательно, на девятом году материки земного шара были бы покрыты одуванчиками по 70 на каждом квадратном метре, если бы огромное большинство семян не погибало бы, не давая ростков.

Известно, что бактерии размножаются делением: одна бактерия делится на две; каждая из этих двух в свою очередь тоже делится на две и т. д. Способность к размножению у бактерий настолько велика, что если бы они не гибли от разных причин, а беспрерывно размножались, то за трое суток общая масса потомства одной только бактерии могла бы составить 7500 тонн!

Интенсивность размножения бактерий активно используют в пищевой промышленности, медицине, сельском и коммунальном хозяйстве, охране природы.

Потомство пары воробьёв при продолжительности жизни в четыре года может покрыть весь земной шар за 35 лет!

Девятое поколение одной пары мух наполнило бы куб, сторона которого равна 140 км, или же составило бы нить, которой можно опоясать земной шар 40 миллиардов раз!

Всего за пять поколений, то есть за 1 – 1,5 летних месяцев, одна единственная тля может оставить более 300 млн. потомков.

В основе раковины улитки лежит интересная математическая кривая, которая называется логарифмическая спираль. Если измерить длины отрезков по оси ОХ, которые получаются, когда спираль пересекает ось, то они образуют геометрическую прогрессию.

Прогрессии в химии

При повышении температуры в арифметической прогрессии, скорость химической реакции вырастает в геометрической прогрессии.

Я решил это проверить и обратился к учителю химии. Проведя ряд опытов, я убедился, что при увеличении температуры в арифметической прогрессии, скорость реакции возрастает в геометрической.

Прогрессии в физике

Деление ядер урана происходит с помощью нейтронов. Нейтрон, ударяя по ядру урана раскалывает его на две части. Получается два нейтрона. Затем два нейтрона, ударяя по двум ядрам, раскалывают их еще на 4 части и т.д. — это геометрическая прогрессия.

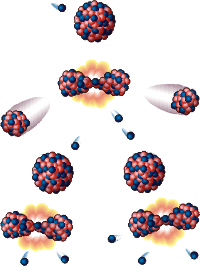
Равноускоренное движение — арифметическая прогрессия, т.к. за каждые равные промежутки времени тело увеличивает скорость в одинаковое число раз.

Прогрессии в литературе

Известный стихотворный размер – ямб обладает свойством: ударение ставится на 2,4, 6,8…слоги. В то же время для хорея ударные 1,3,5, 7… слоги – арифметическая прогрессия.

Пример стихотворения с хореем: «Буря мглою небо кроет…»

Прогрессии в экономике

Денежные вклады под проценты — это пример геометрической последовательности. Зная формулы суммы членов геометрической последовательности, можно подсчитывать сумму на вкладе.

Интересные факты

Игра в шахматы была изобретена в Индии. Царь Ширам был восхищен игрой и приказал наградить изобретателя по-царски. Изобретатель был человеком бедным и когда царь заявил, что выполнит любое его желание, он сказал:

- Хорошо, государь. Прикажи выдать мне за первую шахматную клетку 1 зернышко, за вторую – 2, за третью – 4, за четвертую – 8, за пятую – 16, за шестую – 32 …

Царь только рассмеялся. А мудрецы тем временем взялись за расчёты. И вечером в ужасе предстали пред царём. Оказалось, что бедняк попросил 18 446 744 073 709 551 615 зерен, что равняется 1200 миллиардам тонн.

Английский математик Абрахам де Муавр в престарелом возрасте однажды обнаружил, что продолжительность его сна растёт на 15 минут в день. Составив арифметическую прогрессию, он определил дату, когда она достигла бы 24 часов — 27 ноября 1754 года. В этот день он и умер.

Существует большое количество интересных прогрессий. Вот одна из них: Рассмотрим арифметическую прогрессию из трех членов 1487, 4817, 8147 с шагом 3330. Все числа в ней простые. Но она обладает еще одним интересным свойством - каждое число тройки может быть составлено из цифр другого.

Вписанные друг в друга правильные треугольники — это геометрическая прогрессия.

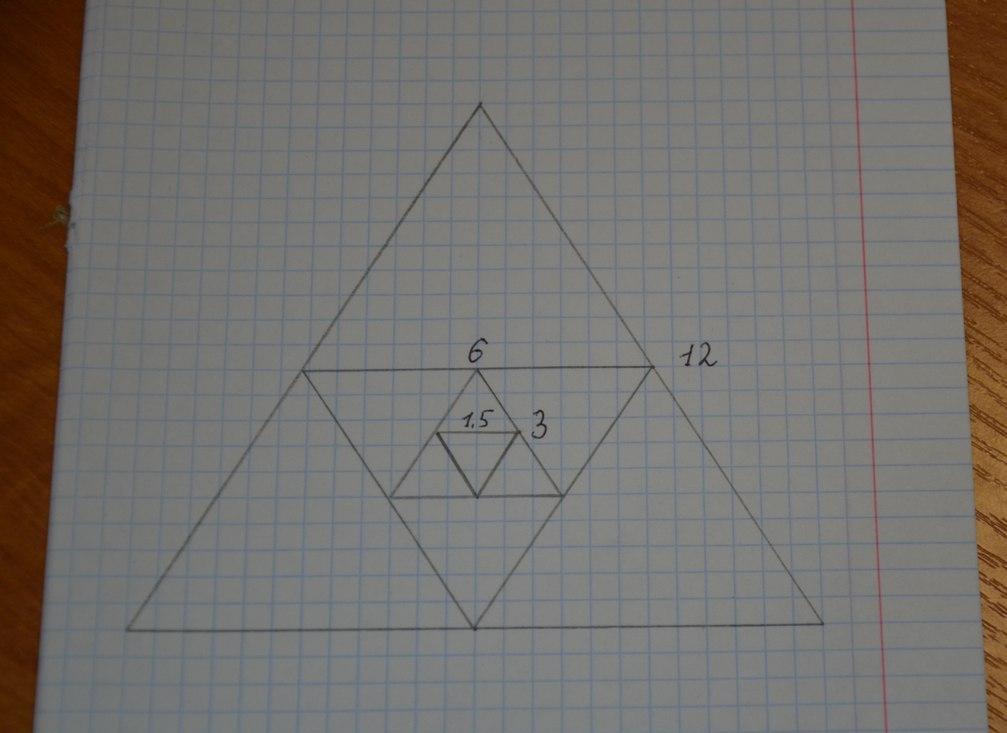
Мне показалось, что треугольники можно вписать по-другому, так, чтобы их стороны не образовывали прогрессии. Однако попробовав начертить их, я убедился в том, что положение фигур относительно друг друга поменять нельзя, а их стороны образуют прогрессию с знаменателем 2.

Анкетирование

Я провел анкетирование среди учащихся 9-ых классов на знание применения прогрессий.

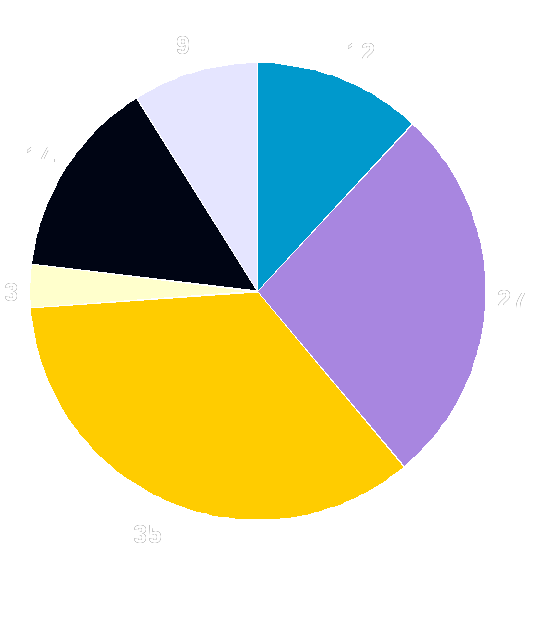
Были опрошены около ста школьников, среди них ничего не знают о прогрессиях – 12%. Остальные дали такие ответы: 27% - рассказали о применении последовательностей в экономике, банковском деле; 35% - привели в пример размножение бактерий; 14% - вспомнили равноускоренное движение; 3% - сказали о связи температуры и скорости протекания химических реакции; 9% - дали другие ответы.

По результатам опроса, больше всего участников приводили в пример размножение бактерий, что говорит о наибольшем распространении данной прогрессии в природе.

Вывод

В ходе исследования, экспериментальным и аналитическим путями я установил:

1. Присутствие прогрессий в природе;

1. Высокую осведомленность школьников о применениях прогрессий;

1. Важность прогрессий в:

1. Физике;

2. Химии;

3. Экономике;

4. Литературе;

1. Имя человека, который дал название прогрессии.

Литература

1. Алгебра А.Г.Мордкович 9 класс, 2011

2. Алгебра Ю.Н. Макарычев 9 класс, 2010

3. Алгебра Ш.А. Алимов 9 класс, 2011

4. Прогрессии, дирекции и ректификация Зиппора Добинс, 1994

5. Вторичные Прогрессии Н.Э. Хастингс, 1998

Источники

1. http://ru.wikipedia.org

2. http://festival.1september.ru

3. http://myshared.ru

4. http://yandex.ru

5. http://project.1september.ru