
ПОСТРОЕНИе ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ

Заполните пропуски в решении
- Выделите полный квадрат двучлена:
а) x² + 2x 7 = x² + 2х + - 8 = (х + ) 2 – 8;
1
1
3
3
х 2
б) x² 6x + 11 = – 2· х + 9 + 2 = (х - ) 2 + 2.
2) Построить график функции y = x² + 4x – 5
вверх
1) Ветви параболы направлены .
2) а) Абсцисса вершины параболы: х 0 = -b/ ; х 0 = /2 = ;
2a
-4
-2
б) Ордината вершины параболы: y 0 = (-2) 2 + 4 - 5 = .
-9
(-2)
Вершина параболы имеет координаты: ( ; – 9 ) .
-2
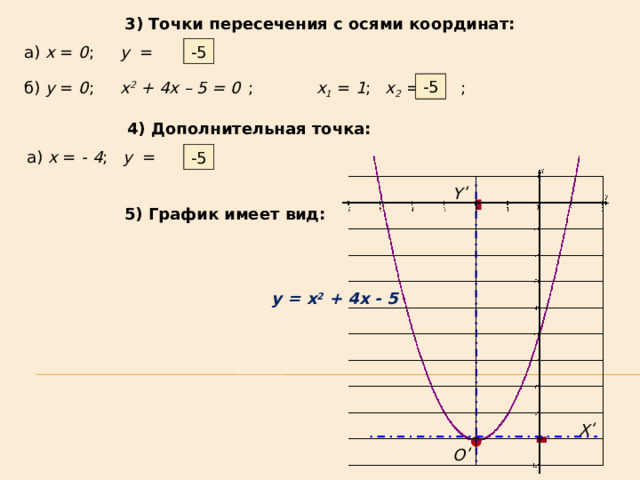
3) Точки пересечения с осями координат:
-5
а) х = 0 ; y = ;
-5
x 1 = 1 ; x 2 = ;
б) y = 0 ; x 2 + 4x – 5 = 0 ;
4) Дополнительная точка:
а) х = - 4 ; y = ;
-5
Yʹ
5) График имеет вид:
y = x 2 + 4x - 5
Xʹ
Oʹ
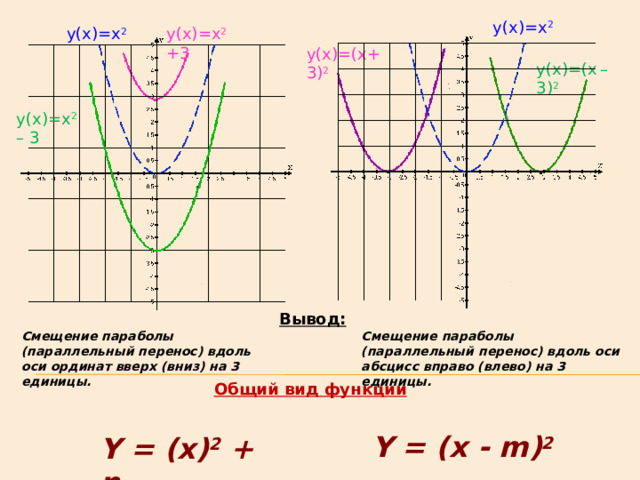
y(x)=x 2
y(x)=x 2
y(x)=x 2 +3
y(x)=(x+3) 2
y(x)=(x – 3) 2
y(x)=x 2 – 3
Вывод:
Смещение параболы (параллельный перенос) вдоль оси ординат вверх (вниз) на 3 единицы.
Смещение параболы (параллельный перенос) вдоль оси абсцисс вправо (влево) на 3 единицы.
Общий вид функции
Y = (x - m) 2
Y = (x) 2 + n
 1, то растяжение по OY Y = (kx) 2 если |k| если |k|1, то сжатие по OX " width="640"
1, то растяжение по OY Y = (kx) 2 если |k| если |k|1, то сжатие по OX " width="640"
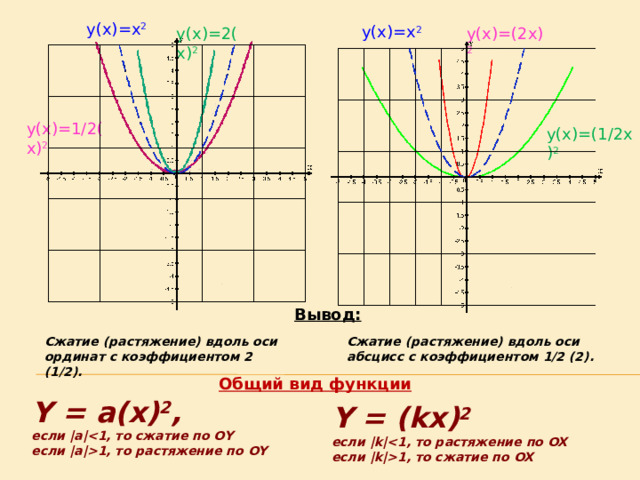
y(x)=x 2
y(x)=x 2
y(x)=(2x) 2
y(x)=2(x) 2
y(x)=1/2(x) 2
y(x)=(1/2x) 2
Вывод:
Сжатие (растяжение) вдоль оси ординат с коэффициентом 2 (1/2).
Сжатие (растяжение) вдоль оси абсцисс с коэффициентом 1/2 (2).
Общий вид функции
Y = a(x) 2 ,
если |а|
если |а|1, то растяжение по OY
Y = (kx) 2
если |k|
если |k|1, то сжатие по OX
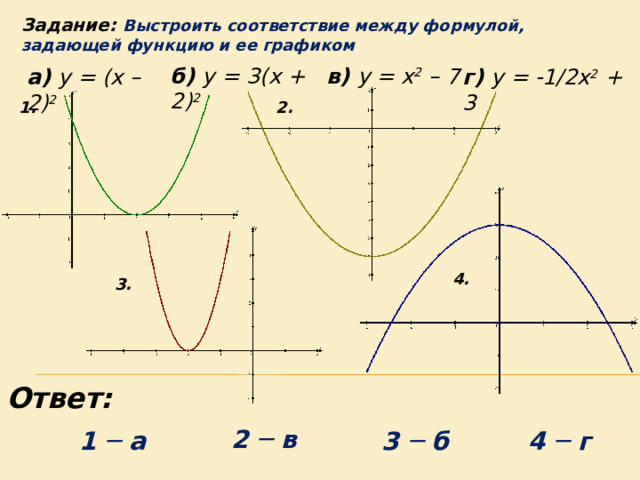
Задание: Выстроить соответствие между формулой, задающей функцию и ее графиком
в) y = x 2 – 7
б) y = 3(x + 2) 2
а) y = (x – 2) 2
г) y = -1/2x 2 + 3
2.
1.
4.
3.
Ответ:
2 ─ в
1 ─ а
3 ─ б
4 ─ г
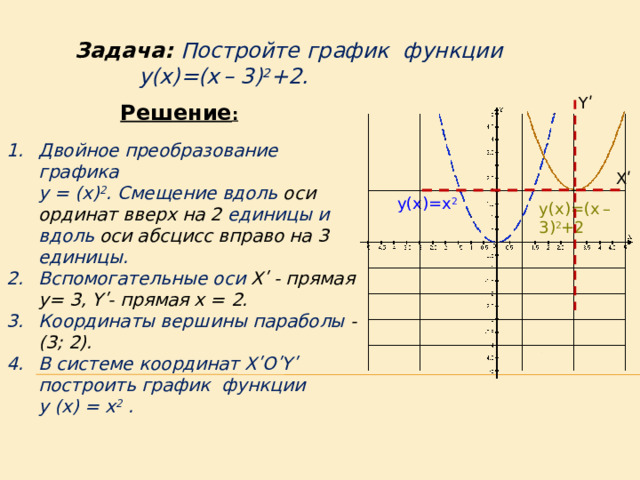
Задача: Постройте график функции y(x)=(x – 3) 2 +2.
Y ʹ
Решение :
- Двойное преобразование графика
y = (x) 2 . Смещение вдоль оси ординат вверх на 2 единицы и вдоль оси абсцисс вправо на 3 единицы.
- Вспомогательные оси X ʹ - прямая y= 3, Y ʹ- прямая x = 2.
- Координаты вершины параболы -(3; 2).
- В системе координат X ʹ O ʹ Y ʹ построить график функции
y (x) = x 2 .
X ʹ
y(x)=x 2
y(x)=(x – 3) 2 +2

Задача:
Постройте график функции y = x 2 + 4x – 5
с помощью преобразований графика y (x) = x ² .
Решение:
1. Выделить полный квадрат двучлена:
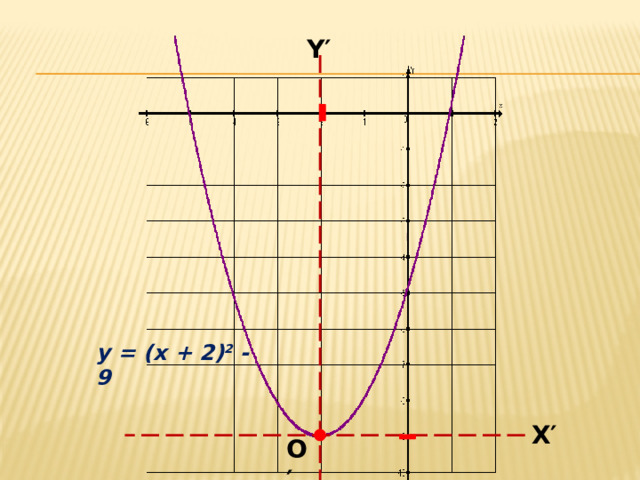
x 2 + 4x – 5 = x 2 + 4x + 4 – 9 = (x+2) 2 – 9.
2. Определить характер смещения графика функции y = (x) 2 : сдвиг вдоль оси абсцисс влево на 2 единицы, вдоль оси ординат – вниз на 9 единиц.
Вывод:
Вершина параболы y = (x) 2 имеет координаты : O΄(-2; -9) .
3. Построить вспомогательную систему координат
X΄O΄Y΄ , где X ʹ- прямая y = -2, Y ʹ- прямая y = -9, O΄(-2; -9) .
4. В новой системе координат X΄O΄Y΄ построить график функции y = (x) 2 .
Y′
y = (x + 2) 2 - 9
X′
О′

Алгоритм построения графика квадратичной функции путем преобразований.
1 . Применить к трехчлену y(x) = ax 2 + bx + c метод выделения полного квадрат двучлена;
2. По формуле y(x)= a(x – m) 2 + n определить характер преобразования графика;
3. Перейти к вспомогательной системе координат X΄O΄Y΄, где Xʹ - прямая y = m, Yʹ - прямая x = n, O΄(m; n);
4. К новой системе координат «привязать» график функции y(x) = ax 2 .

Выберите вариант самостоятельной
работы соответствующий вашим ощущениям.
А: все понятно,
буду смело применять
3 вариант
В: есть некоторые сомнения
2 вариант
С: пока еще много вопросов
1 вариант

Самостоятельная работа с раздаточным Материалом
2 вариант .
3 вариант.
1 вариант.
1. График, какой функции получится, если параболу
функции получится, если
y = (x)² перенести
получится, если параболу
a) на 2 единицы масштаба вправо;
параболу
y = (x)² перенести
y = (x)² перенести
b) на 3 единицы масштаба вниз и на 1 – влево;
a) на 3 единицы масштаба вправо;
c) на 0,5 единицы масштаба вправо и на 2,5 – вверх?
b) на 4 единицы масштаба вниз.
c) на 2 единицы масштаба влево и на 1,5 – вверх?
2. Найдите координаты вершины параболы.
масштаба влево;
a) y = (x + 17)²
2. Найдите координаты вершины параболы.
b) на 3 единицы
b) y = (2x)² – 21
a) y = (x + 7)²
масштаба вверх;
c) на 2,5 единицы масштаба вправо и
c) y = 1/2 (x – 12)² + 9
b) y = (x)² – 11
3. Постройте график функции.
на 1 – вниз?
c) y = 3(x – 12)² + 19
2. Найдите координаты
3. Постройте график функции.
a) y = –3(x + 2,5)² – 4
a) y = – (x – 2)² + 4
вершины параболы.
b) y = x² – 8x + 15
b) y = x² – 4x + 1
a) y = (x – 7)²
b) y = (x)² + 11
c) y = (x + 12)² - 19
3. Постройте график функции.
a) y = (x + 2)² - 4
b) y = x² + 6x + 9
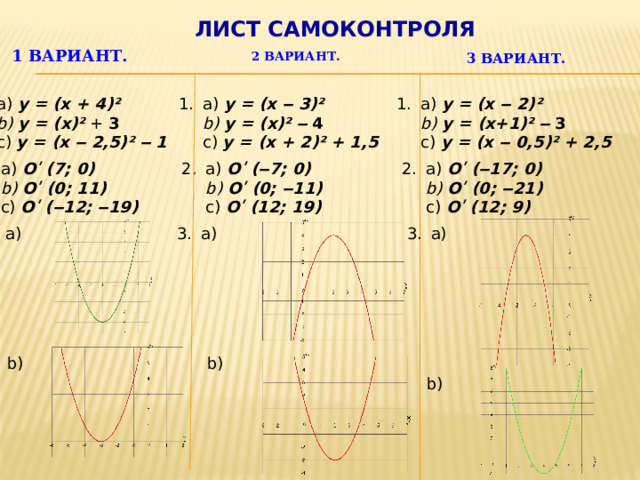
Лист самоконтроля
1 вариант.
3 вариант.
2 вариант.
b) y = (x)² + 3
b) y = (x+1)² ‒ 3
b) y = (x)² ‒ 4
c) y = (x ‒ 2,5)² ‒ 1
c) y = (x ‒ 0,5)² + 2,5
c) y = (x + 2)² + 1,5
2. a) O ʹ (7; 0)
2. a) O ʹ (‒7; 0)
2. a) O ʹ (‒17; 0)
b) O ʹ (0; ‒21)
b) O ʹ (0; ‒11)
b) O ʹ (0; 11)
c) O ʹ (12; 19)
c) O ʹ (‒12; ‒19)
c) O ʹ (12; 9)
3. a)
3. a)
3. a)
b)
b)
b)

Итог урока:
1. Дискуссия на тему: «Преимущества и недостатки изученного метода построения графиков функций».
2. Воспроизведите этапы алгоритма построения графика квадратичной функции методом преобразований.
3. Выберите смайлик соответствующий вашим ощущениям.
А: все понятно,
С: пока еще много вопросов
В: есть некоторые сомнения
буду смело применять

Домашнее задание:
.
Постройте график функции
у(x)=|x ‒ 3| + 4 и найти наименьшее значение функции.











 1, то растяжение по OY Y = (kx) 2 если |k| если |k|1, то сжатие по OX " width="640"
1, то растяжение по OY Y = (kx) 2 если |k| если |k|1, то сжатие по OX " width="640"





























