"Построение сечений многоугольников." в 10-11классах.

«О методах построения сечений.» в10-11классах.

МБОУ «Мирновская средняя школа г. Евпатории Республики Крым» Учитель Елаш Т.П.

Сечение куба

Задача 1

β

α

2

2

Определение сечения.

• Секущей плоскостью многогранника назовем любую плоскость, по обе стороны от которой имеются точки данного многогранника.

• Секущая плоскость пересекает грани многогранника по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника .

Секущая плоскость

А

N

M

α

K

D

В

С

A

сечение

Секущая плоскость

N

M

α

K

D

B

C

На каких рисунках сечение построено не верно?

D

D

D

M

M

А

А

C

C

C

А

M

B

B

B

D

D

P

P

N

N

Q

Q

А

C

C

А

S

M

M

B

B

Построить сечение тетраэдра плоскостью, заданной тремя точками. Задача 2 и 3

D

D

M

N

M

P

L

А

С

А

С

P

N

В

В

Построение:

Построение:

• Построение:

1. Отрезок MN

1. Отрезок MP

• 1. Отрезок MP

2. Луч NP;

луч NP пересекает АС в точке L

2. Отрезок PN

• 2. Отрезок PN

3. Отрезок MN

• 3. Отрезок MN

3. Отрезок ML

MPN – искомое сечение

• MPN – искомое сечение

MNL –искомое сечение

Построить сечение тетраэдра плоскостью, заданной тремя точками. Задача 4

D

Построение:

• Построение:

1. Отрезок NQ

• 1. Отрезок NQ

P

2. Отрезок NP

• 2. Отрезок NP

Прямая NP пересекает АС в точке Е

• Прямая NP пересекает АС в точке Е

3. Прямая EQ

• 3. Прямая EQ

EQ пересекает BC в точке R

• EQ пересекает BC в точке R

NQRP – искомое сечение

• NQRP – искомое сечение

N

С

А

E

R

Q

В

Построить сечение тетраэдра плоскостью, заданной тремя точками. Задача 5

D

Построение:

1. MN; отрезок МК

2. MN пересекает АВ в точке Х

3. ХР; отрезок SL

MKLS – искомое сечение

M

N

S

А

C

P

K

L

B

X

Аксиоматический метод

Метод следов

• Метод следов

Суть метода заключается в построении вспомогательной прямой, являющейся изображением линии пересечения секущей плоскости с плоскостью какой-либо грани фигуры . Удобнее всего строить изображение линии пересечения секущей плоскости с плоскостью нижнего основания. Эту линию называют следом секущей плоскости. Используя след, легко построить изображения точек секущей плоскости, находящихся на боковых ребрах или гранях фигуры .    

Постройте сечение пирамиды плоскостью, проходящей через три точки M,N,P. Задача 6

F

M

P

D

А

Y

N

S

C

B

XY – след секущей плоскости

на плоскости основания

Z

X

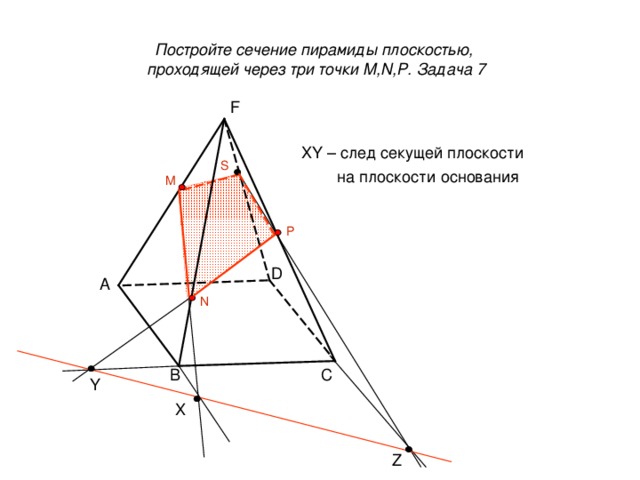
Постройте сечение пирамиды плоскостью, проходящей через три точки M,N,P. Задача 7

F

XY – след секущей плоскости

на плоскости основания

S

M

P

D

А

N

B

C

Y

X

Z

Геометрические понятия

• Плоскость – грань
• Прямая – ребро
• Точка – вершина

вершина

грань

ребро

Многогранники

• Тетраэдр

• Параллелепипед

15

15

Геометрические утверждения

• Если две точки одной прямой лежат в плоскости, то и

вся прямая лежит в этой плоскости.

16

16

Геометрические утверждения

• Если две параллельные плоскости пересечены третьей, то

линии их пересечения параллельны.

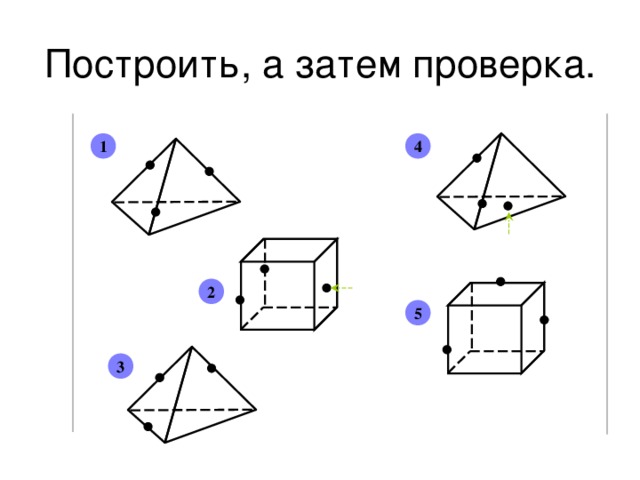
Построить, а затем проверка.

1

4

2

5

3

18

18

Решение. Задача 8

1

19

19

Решение. Задача 9

2

Решение. Задача 10

3

Решение. Задача 11

4

Решение. Задача12

5

Задача №13

1

Решение задачи №13

1

Задача №14

2

Решение задачи №14

2

Спасибо за внимание