Урок 12.
Площадь криволинейной трапеции.
Цели урока: знать правила нахождении первообразных, понятие криволинейной трапеции, формулу для нахождения площади криволинейной трапеции. Уметь вычислять площадь фигуры, ограниченной линиями.
Ход урока.
1. Организационный момент.
2. Индивидуальный опрос и фронтальная работа с классом.
На доске начерчена таблица, вызвать одного ученика для ее заполнения.
| № | Функция | Первообразная |
| 1 | 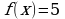
| 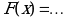
|
| 2 | 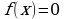
| 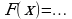
|
| 3 | 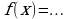
| 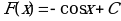
|
| 4 | 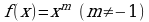
| 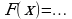
|
| 5 | 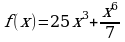
| 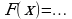
|
| 6 | 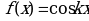
| 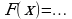
|
| 7 | 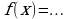
| 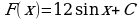
|
| 8 | 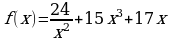
| 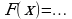
|
| 9 | 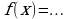
| 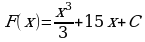
|
| 10 | 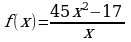
| 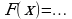
|
Остальные учащиеся следующее задания:
1) Повторить сведения о преобразованиях графиков
2) Являются ли первообразными для одной и той же функции следующие функции:
а) 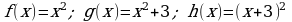
б) 
в) 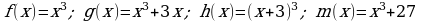
г) 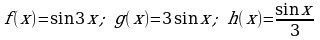
3. Объяснение нового материала.
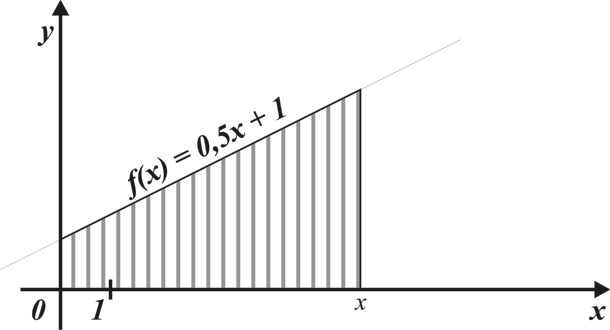
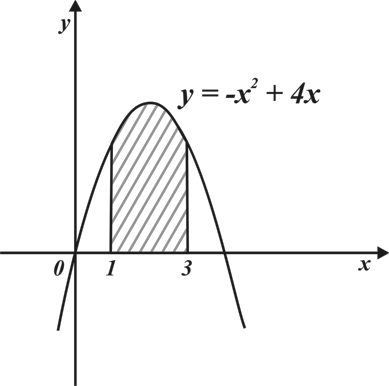
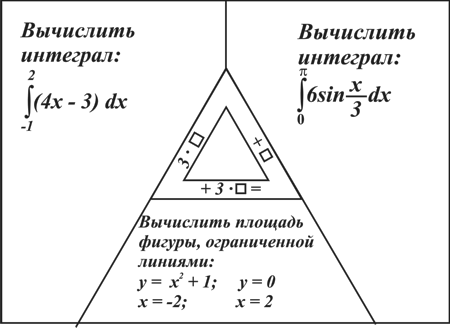
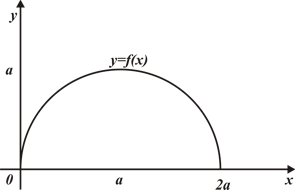
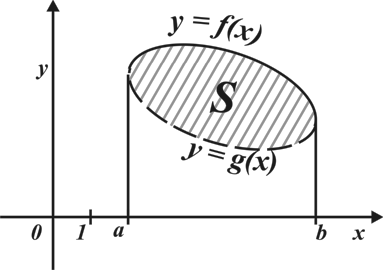
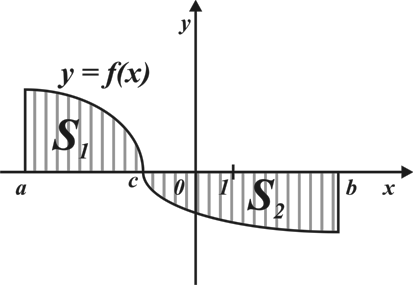
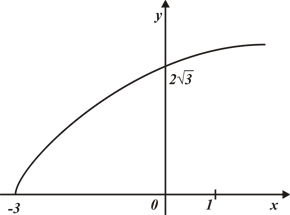
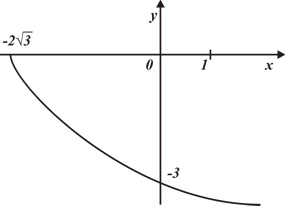
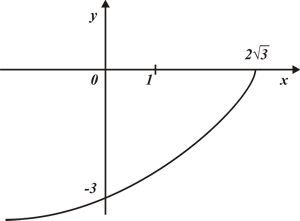
Материал параграфа дается на наглядно-интуитивном уровне, поэтому учителю не следует требовать от учащихся воспроизведения доказательства теоремы о площади. Это доказательство можно прочесть на уроке, после рассмотрения понятия криволинейной трапеции. Представление о криволинейной трапеции учащиеся должны получить, изучая рис. 119 (стр. 185), а - д. Можно перенести их на кодопленку или таблицу. Рассматривая рисунки, выделять график функции на отрезке [a; b], прямые (а затем точки с абсциссами) 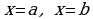 , ось OX, учащиеся выявят особенности фигуры, которая называется криволинейной трапецией. Рассмотреть пример. Вычислить площадь криволинейной трапеции, ограниченной графиком функции
, ось OX, учащиеся выявят особенности фигуры, которая называется криволинейной трапецией. Рассмотреть пример. Вычислить площадь криволинейной трапеции, ограниченной графиком функции 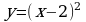 , прямыми
, прямыми 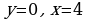 и
и 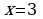 . Решая это простое задание напомнить учащимся, что данную параболу можно строить двумя способами:
. Решая это простое задание напомнить учащимся, что данную параболу можно строить двумя способами:
1) преобразовывая график функции 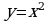 , смещая его вдоль оси OX на две единицы вправо.
, смещая его вдоль оси OX на две единицы вправо.
2) вычисляя вершину параболы 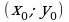 по формуле , затем находя несколько контрольных точек.
по формуле , затем находя несколько контрольных точек.
Для функции 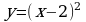 одной из первообразных является функция
одной из первообразных является функция 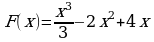 .
.
Значит , 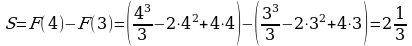 .
.
Ответ: 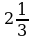
4. Закрепление нового материала.
Решить №353(в, г), 354(в, г).
5. Задание из ЕГЭ.
Задание 1В:
Найдите значение выражения 2S, если S – площадь фигуры ограниченной линиями 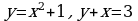 .
.
Ответ: 9
6. Итоги урока.
7. Домашнее задание.
Прочитать и разобрать §29.
Решить следующие задачи №353(а, б), 354(а, б).
Урок 13.
Площадь криволинейной трапеции.
Цели урока: знать понятие криволинейной трапеции, правила нахождения первообразных, формулу для вычисления площади криволинейной трапеции. Уметь вычислять площадь фигуры, ограниченной линиями, строить графики в координатной плоскости, выполняя их преобразования.
Ход урока.
1. Организационный момент.
2. Индивидуально задание по карточкам.
Раздаются в начале урока на 8-10 минут.
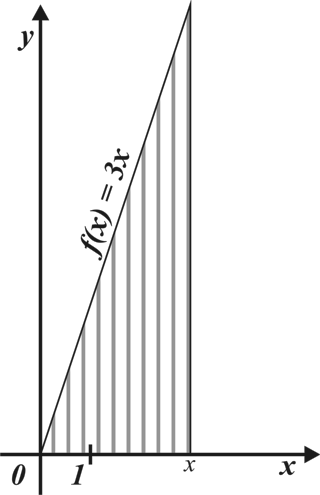
| 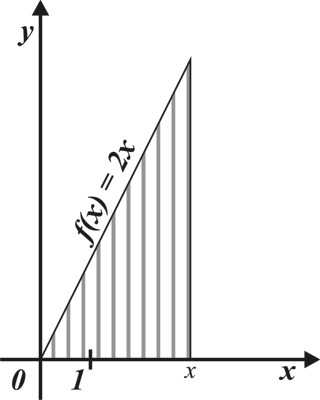
| Запишите формулу, выражающую площадь S(x) фигуры, заштрихованной на рисунке, как функцию от х. Вычислив производную, покажите, что 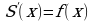
|
| 
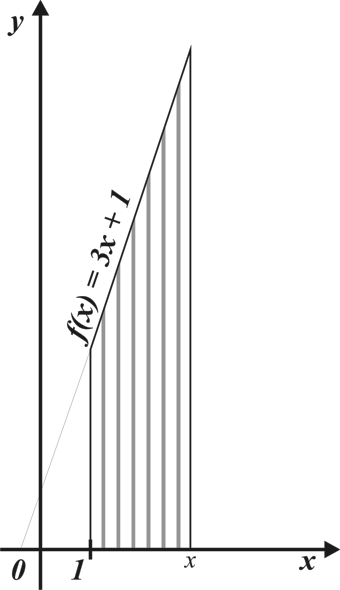
| Запишите формулу, выражающую площадь S(x) фигуры, заштрихованной на рисунке, как функцию от х. Вычислив производную, покажите, что 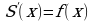
|
| 
| Запишите формулу, выражающую площадь S(x) фигуры, заштрихованной на рисунке, как функцию от х. Вычислив производную, покажите, что 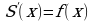
|
| 
| Запишите формулу, выражающую площадь S(x) фигуры, заштрихованной на рисунке, как функцию от х. Вычислив производную, покажите, что 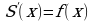
|
Вычислите площадь фигуры, ограниченной линиями 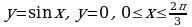 , используя формулу
, используя формулу 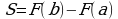 .
.
Вычислите площадь фигуры, ограниченной линиями 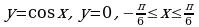 , используя формулу
, используя формулу 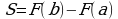 .
.
Вычислите площадь фигуры, ограниченной линиями 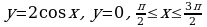 , используя формулу
, используя формулу 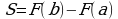 .
.
Вычислите площадь фигуры, ограниченной линиями 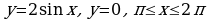 , используя формулу
, используя формулу 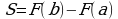 .
.
3. Устная работа.
Остальные учащиеся выполняют следующие задания.
Определить функцию, которую можно записать вместо многоточия.
а) 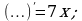 б)
б) 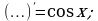 в)
в) 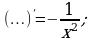
г) 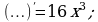 д)
д) 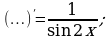 е)
е) 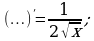
ж) 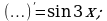 з)
з) 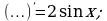 и)
и) 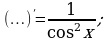
Найти площадь заштрихованной фигуры.
| а) | 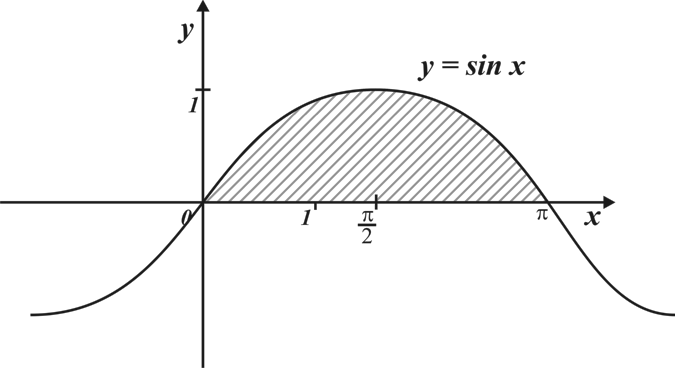
|
| б) | 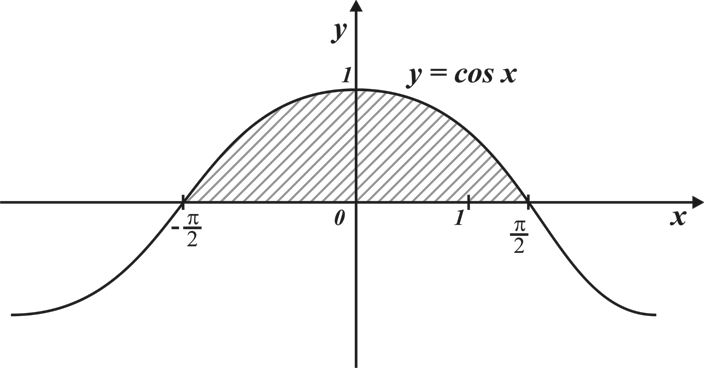
|
4. Решение задач.
Разобрать №355(в, г), 356(а, б).
5. Самостоятельная работа.
Вариант I.
Найти площадь фигуры, ограниченной линиями
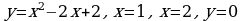
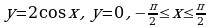
Вариант II.
Найти площадь фигуры, ограниченной линиями
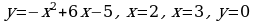
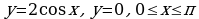
6. Задание из ЕГЭ.
Задание 1С:
Найдите множество значений функции 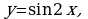 если
если 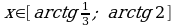
Решение:
Наша задача эквивалентна следующему заданию. Найти 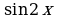 для значений на концах отрезка области определения.
для значений на концах отрезка области определения.
Если 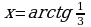 , то
, то 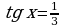 ,
, 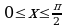 , т.е.
, т.е.
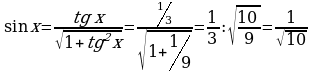
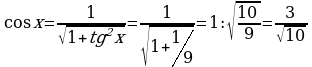
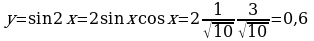
Если 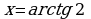 , то
, то 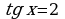 ,
, 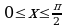 , т.е.
, т.е.
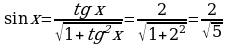
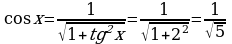
 .
.
Известно, что 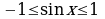 . Максимум функции
. Максимум функции 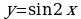 принадлежит данному отрезку
принадлежит данному отрезку 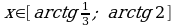 , значит наибольшее значение функции на этом отрезке равно 1. Следовательно, множество значений функции на данном отрезке [0,6; 1].
, значит наибольшее значение функции на этом отрезке равно 1. Следовательно, множество значений функции на данном отрезке [0,6; 1].
Ответ: [0,6; 1]
7. Итоги урока.
8. Домашнее задание.
Прочитать и разобрать §29.
Решить следующие задачи №355(а, б), 356(в, г).
Урок 14.
Интеграл. Формула Ньютона-Лейбница.
Цели урока: знать понятие криволинейной трапеции, понятие интеграла, формулу Ньютона-Лейбница, правила нахождения первообразных. Уметь вычислять интегралы.
Ход урока.
1. Организационный момент.
2. Устная работа.
1) Найти все первообразные функции.
а) 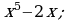 б)
б) 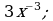 в)
в) 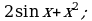
г) 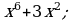 д)
д) 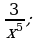 е)
е) 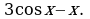
2) Найти площадь фигуры, ограниченной линиями.
а) 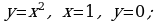
б) 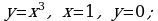
в) 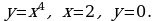
Это задание следует сопроводить готовыми чертежами.
3. Объяснение нового материала.
Новая тема дается согласно материалам учебника (стр. 188-190) в виде лекции. Рисунки 122, 123 заготовить заранее на доске или на плакате. Формула Ньютона-Лейбница вводится на одном уроке с термином «интеграл». Учащиеся рассматривают интеграл как разность значений первообразных, преподаватель подробно объясняет обозначение и чтение, затем переходит к записи формулы нахождения площади через интеграл. Не следует усиливать трудность знакомства со столь сложным понятием и здесь же говорить об интеграле сумм: этот материал не является обязательным для всех учащихся. В курсе математике средней школы нет понятия неопределенного интеграла, поэтому определенный интеграл называют просто интегралом. Интегральная сумма рассматривается в общем виде и предназначена только для ознакомлением с понятием интеграла. Желательно если учащиеся (если учитель счел возможным ознакомить их с этим материалом) поняли, что об интегральной сумме функции на отрезке, а затем и интеграле можно говорить и в том случае, когда функция не только непрерывна и положительна, но и принимает на этом отрезке любые значения, в том числе и отрицательные, и нуль.
Записать итоговую формулу:
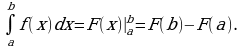
4. Закрепление нового материала.
Разобрать следующие примеры:
1) 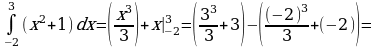
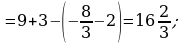
2) 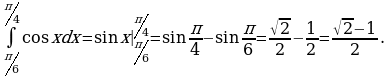
Далее разобрать №357(в, г), 358(в, г), 359(в, г), 362(в, г).
5. Итоги урока.
6. Домашнее задание.
Прочитать и разобрать §30.
Решить следующие задачи №358(а, б), 359(а, б).
Урок 15.
Интеграл. Формула Ньютона-Лейбница.
Цели урока: знать понятие криволинейной трапеции, понятие интеграла, формулу Ньютона-Лейбница. Уметь вычислять интегралы, находить площади фигур, ограниченной линиями с помощью интеграла.
Ход урока.
1. Организационный момент.
2. Проверочная работа.
Вычислить интегралы.
| Вариант 1. | Вариант 2. |
| 1) 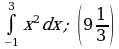 | 1) 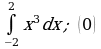 |
| 2) 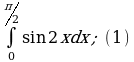 | 2) 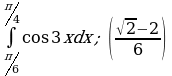 |
| 3) 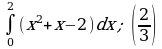 | 3) 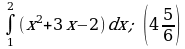 |
| 4) 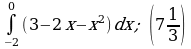 | 4) 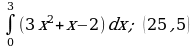 |
| 5) 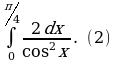 | 5) 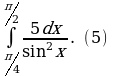 |
В скобках даны ответы. Эту работу следует проверить сразу же на уроке при помощи кодоскопа.
3. Решение задач.
Решить: №360, 361(в, г), 364(а, б).
4. Задание из ЕГЭ.
Задание В:
Вычислить площадь фигуры, ограниченной прямой 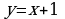 и параболой
и параболой 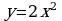 .
.
Решение:
Найдем абсциссы точек пересечения графиков.
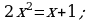
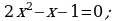
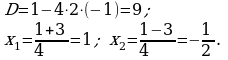
Построим в одной системе координат графики двух функций.
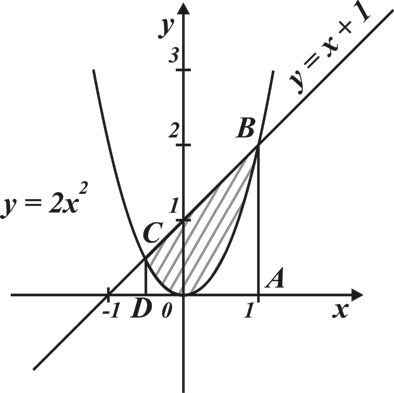
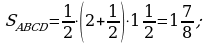
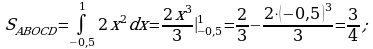
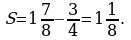
Ответ: 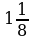 .
.
5. Итоги урока.
6. Домашнее задание.
Прочитать и разобрать §30.
Решить следующие задачи №364(в, г).
Урок 16.
Интеграл. Формула Ньютона-Лейбница.
Цели урока: знать понятие криволинейной трапеции, понятие интеграла, формулу Ньютона-Лейбница. Уметь вычислять интегралы, находить площади фигур, ограниченной линиями с помощью интеграла.
Ход урока.
1. Организационный момент.
2. Устная работа.
Повторить понятие криволинейной трапеции, формулу Ньютона-Лейбница, формулы площади следующих фигур: прямоугольника, треугольника и трапеции.
3. Объяснение нового материала.
Записать в тетрадях и на доске основные формулы для работы с интегралом.
1) 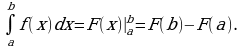
2) 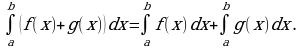
(Линейность интеграла.)
3) 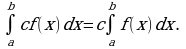
4) 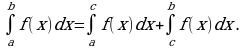
(Аддитивность интеграла.)
Последние три случая лучше поместить на плакате.
4. Закрепление нового материала.
Решить: № 365(а, б), 366(а), 367.
5. Задание из ЕГЭ.
Задание 1С:
Из множества значений функции
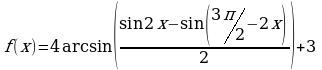
удалить все целые числа. Сколько получится промежутков?
Решение:
Используя формулу 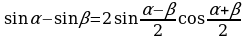 , получим
, получим 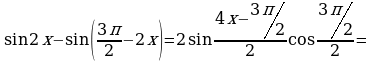
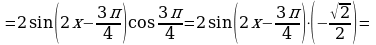
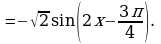
Значит, 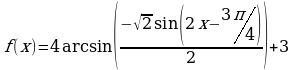 . Множество значений функции
. Множество значений функции 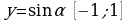 . Используем запись двойного неравенства для записи множества значений.
. Используем запись двойного неравенства для записи множества значений.
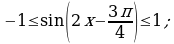
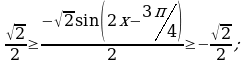
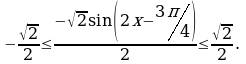
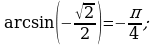
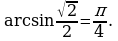
Значит 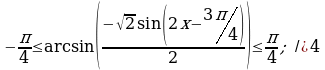
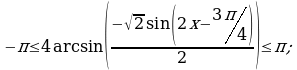
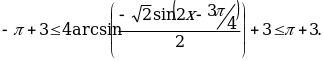
Следовательно, 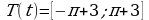 . Удалим целые числа из множества значений и посчитаем количество числовых промежутков, используем для этого координатную прямую.
. Удалим целые числа из множества значений и посчитаем количество числовых промежутков, используем для этого координатную прямую.
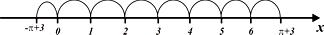
Наглядно видно, что числовых промежутков 8.
Ответ: 8.
6. Итоги урока.
7. Домашнее задание.
Прочитать и разобрать §30.
Решить следующие задачи №365(в, г).
Урок 17.
Интеграл. Формула Ньютона-Лейбница.
Цели урока: знать понятие криволинейной трапеции, понятие интеграла, формулу Ньютона-Лейбница. Уметь вычислять интегралы, находить площади фигур, ограниченной линиями с помощью интеграла.
Ход урока.
1. Организационный момент.
2. Решение задач.
Разобрать задачи: № 366(б), 368.
3. Самостоятельная работа.
Вычислить (предварительно сделав рисунок) площадь фигуры, ограниченной линиями.
| Вариант 1. | Вариант 2. |
| 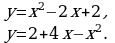
| 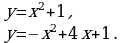
|
| Ответ: 9. | Ответ: 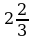 . . |
4. Задание из ЕГЭ.
Задание 1В:
Вычислите площадь фигуры, ограниченной линиями 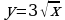 и
и 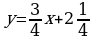 .
.
Решение:
Найдем абсциссы точек пересечения графиков.
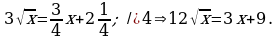
Пусть 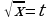 , тогда
, тогда 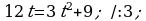
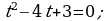
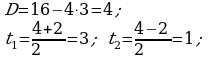
Если 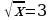 , то
, то 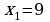 .
.
Если 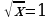 , то
, то 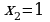 .
.
Построим в одной системе координат графики двух функций.
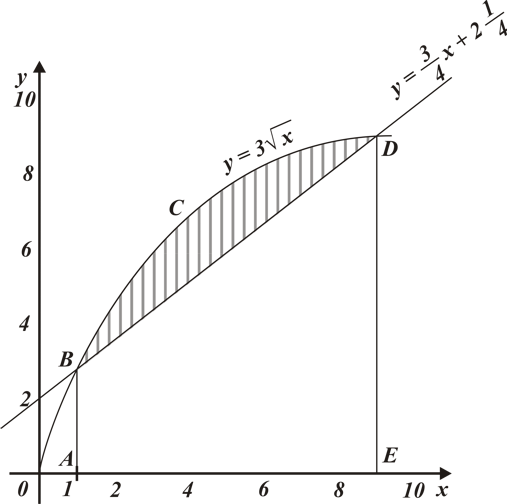
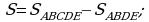
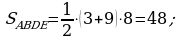
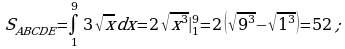
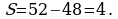
Ответ:4.
5. Итоги урока.
6. Домашнее задание.
Прочитать и разобрать §30.
Решить следующие задачи №366(в, г).
Урок в 11 классе.
Применение интеграла.
Цели урока: знать сферы применения интеграла, правила вычисления производных и первообразных. Уметь вычислять интегралы и решать прикладные задачи с интегралами.
Ход урока.
1. Организационный момент.
2. Объяснение нового материала.
При знакомстве с интегралом мы выделили три его характеристики.
Интеграл от функции f есть площадь ее под графиком (с учетом знака).
Интеграл есть придел интегральных сумм.
Интеграл от функции f есть приращение первообразной.
Любая из этих характеристик интеграла может служить основой для его приложений. Вычисление площади самое простое применение интеграла, так как интеграл по определению тесно связан с площадью. Вычисление некоторых физических величин с помощью интеграла потребует дополнительных рассуждений. К величинам, которые вычисляются с помощью интеграла, относятся: перемещение и работа, масса и электрический заряд, площадь и объем. Последние величины обладают общими свойствами:
Величины можно рассматривать как функции отрезков.
Для вычисления этих величин с помощью интеграла нужно знать скорость изменения этих величин.
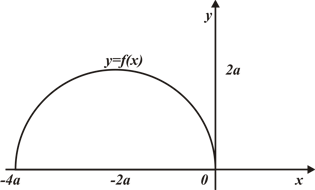
Рассмотрим самую распространенную задачу из приложений интеграла: вычисление объемов тел. Материал учебника можно дополнить следующими рассуждениями.
Пусть дано тело объемом V, причем имеется такая прямая, что для любой плоскости (рис. 125 стр. 194), перпендикулярной данной прямой, известна площадь сечения S тела этой плоскостью. Но плоскость перпендикулярная оси ОХ, пересекает ее в некоторой точке x. Следовательно, каждому числу x 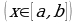 поставлено в соответствии единственное число
поставлено в соответствии единственное число 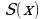 - площадь сечения тела этой плоскостью. Имеется функция
- площадь сечения тела этой плоскостью. Имеется функция 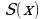 , заданная на отрезке
, заданная на отрезке 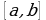 .
.
Если функция непрерывна на отрезке 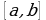 , то справедлива формула
, то справедлива формула 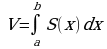 .
.
Тело, полученное вращением криволинейной трапеции, ограниченной графиком непрерывной и неотрицательной на отрезке 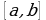 функцией, отрезками прямых
функцией, отрезками прямых 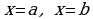 и отрезком
и отрезком 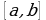 оси ОХ, имеем объем, выражающийся по формуле:
оси ОХ, имеем объем, выражающийся по формуле:
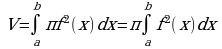 .
.
Д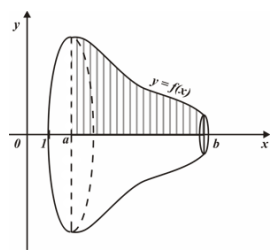 ействительно, каждая плоскость, перпендикулярная оси ОХ и пересекающая отрезок
ействительно, каждая плоскость, перпендикулярная оси ОХ и пересекающая отрезок 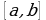 этой оси в точке x, дает в сечении круг радиуса f(x). Соответственно, площадь сечения равна площади круга радиуса f(x):
этой оси в точке x, дает в сечении круг радиуса f(x). Соответственно, площадь сечения равна площади круга радиуса f(x): 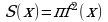 .
.
На рисунке показан объем тела, полученного вращением криволинейной трапеции.
Для всех остальных применений интеграл в физических задачах удобно составить следующую таблицу.
| Величины | Вычисление производной | Вычисление интеграла |
| A – работа; F – сила; N – мощность; x – перемещение; t – время. | 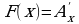
| 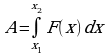
|
| m – масса тонкого стержня; 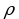 - линейная плотность; - линейная плотность;
x - перемещение. | 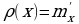
| 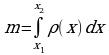
|
| q – электрический заряд; I – сила тока; t – время. | 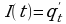
| 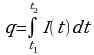
|
| S – перемещение; U – скорость; t – время. | 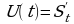
| 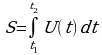
|
| Q – количество теплоты; C – теплоемкость; t – время. | 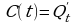
| 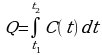
|
Задача на нахождение центра масс рассмотрена в учебнике (стр. 197-198).
3. Закрепление нового материала.
Решить: № 370(а, б), 373, 377.
4. Задание из ЕГЭ.
Задание 1В:
Вычислите площадь фигуры, ограниченной линиями 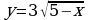 и
и 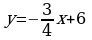 .
.
Решение:
Н айдем абсциссы точек пересечения графиков.
айдем абсциссы точек пересечения графиков.
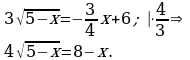
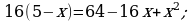
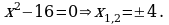
Построим в одной системе координат графики двух функций.
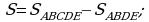
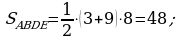
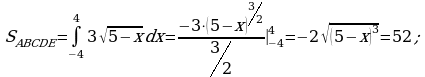
Ответ:4.
5. Итоги урока.
6. Домашнее задание.
Прочитать и разобрать §31.
Решить следующие задачи №370(в, г), 376.
Урок в 11 классе.
Применение интеграла.
Цели урока: подготовиться к контрольной работе по теме «Первообразная и интеграл».
Ход урока.
1. Организационный момент.
2. Устная работа.
Повторить определение первообразной, основное свойство первообразной, правила нахождения первообразных, понятие интеграла, формулу Ньютона-Лейбница.
Решить следующие задания.
Найдите общий вид первообразных для функций.
а) 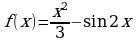 на промежутке
на промежутке  .
.
1) 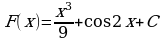 ; 2)
; 2) 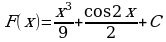 ;
;
3)  ; 4)
; 4) 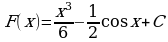 .
.
б) 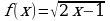 на промежутке
на промежутке 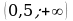 .
.
1) 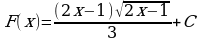 ;
;
2) 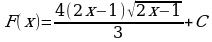 ;
;
3) 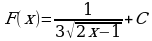 ;
;
4) 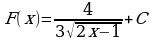 .
.
Найдите производную функции:
а) 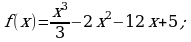 б)
б) 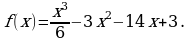
Дана функция 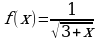 . Укажите график функции
. Укажите график функции 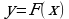 , если
, если 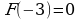 .
.
3. Решение задач.
1) Для функции 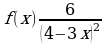 найдите ее первообразную, если
найдите ее первообразную, если 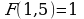 .
.
Ответ: 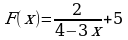 .
.
2) Известно что 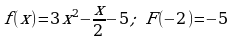 , найдите
, найдите 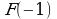 .
.
Ответ: 7,75.
3) Найдите площадь фигуры, заключенной между дугами линий 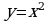 и
и 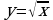 .
.
Ответ: 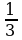 .
.
4. Задание из ЕГЭ.
Задание 1В:
При каком натуральном значении параметра 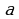 . уравнение
. уравнение 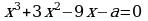 имеет ровно два корня?
имеет ровно два корня?
Решение:
Запишем уравнение в виде 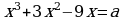 . Найдем решение графическим способом. Построим в одной системе координат графики функций
. Найдем решение графическим способом. Построим в одной системе координат графики функций 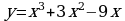 и
и 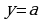 .
.
1) 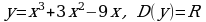
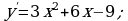
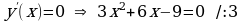
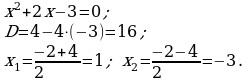
Критические точки: 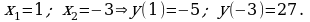
Определим знаки производной.

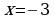 - точка максимума.
- точка максимума.
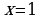 - точка минимума.
- точка минимума.
Изобразим схематично график функций.
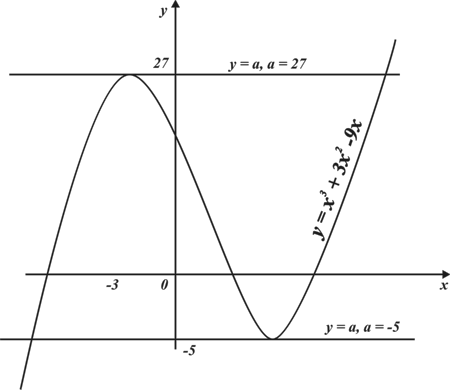
2) 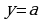 - прямая параллельная оси ОХ, проходящая через точку
- прямая параллельная оси ОХ, проходящая через точку 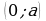 .
.
Два данных графика будут иметь две общие точки, если 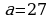 или
или 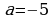 .
.
Натуральное значение параметра 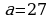 .
.
Ответ: 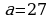 .
.
5. Итоги урока.
6. Домашнее задание.
Решить следующие задачи: стр. 205 №1(2), 2(3).
Урок в 11 классе.
Контрольная работа №1.
Цели урока: проконтролировать знания учащихся.
Ход урока.
1. Организационный момент.
2. Контрольная работа.
Вариант 1.
1) Докажите, что функция 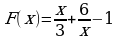 есть первообразная для функции
есть первообразная для функции 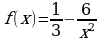 на промежутке
на промежутке 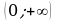 .
.
2) Известно, что функция 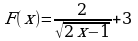 есть первообразная для функции f(x) на промежутке
есть первообразная для функции f(x) на промежутке 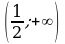 . Найти f(x).
. Найти f(x).
3) Для функции 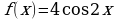 найдите:
найдите:
а) общий вид первообразных;
б) первообразную график, которой проходит через точку 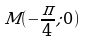 .
.
4) Вычислите площадь фигуры, ограниченной линиями 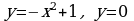 .
.
5) Найдите все первообразные функции 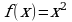 , графики которых имеют ровно две общие точки с графиком функции
, графики которых имеют ровно две общие точки с графиком функции 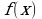 .
.
Вариант 2.
1) Докажите, что функция 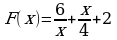 есть первообразная для функции
есть первообразная для функции 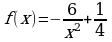 на промежутке
на промежутке 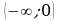 .
.
2) Известно, что функция 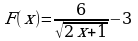 есть первообразная для функции f(x) на промежутке
есть первообразная для функции f(x) на промежутке 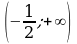 . Найти f(x).
. Найти f(x).
3) Для функции 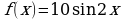 найдите:
найдите:
а) общий вид первообразных;
б) первообразную график, которой проходит через точку 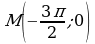 .
.
4) Вычислите площадь фигуры, ограниченной линиями 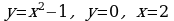 .
.
5) Найдите все первообразные функции 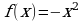 , графики которых имеют ровно две общие точки с графиком функции
, графики которых имеют ровно две общие точки с графиком функции 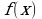 .
.
РЕШЕНИЕ:
Вариант 1.
1) 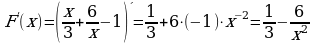 , то есть
, то есть 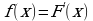 . Значит,
. Значит, 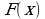 - первообразная для функции
- первообразная для функции 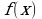 .
.
2) 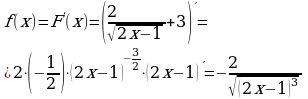
3) 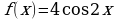
а) 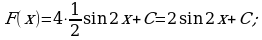
б) 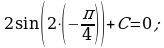
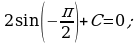
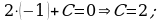
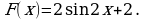
4)
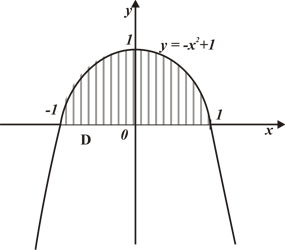
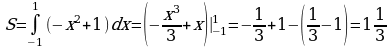
Ответ: 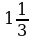 .
.
5) Общий вид первообразных 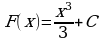 . Задача сводится к нахождению параметра С, когда уравнение
. Задача сводится к нахождению параметра С, когда уравнение 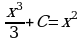 имеет два корня.
имеет два корня. 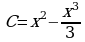
Рассмотрим функции 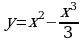 и
и 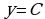 .
.
1) 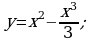
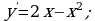
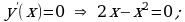
Критические точки: 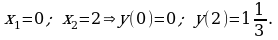
Определим знаки производной.

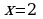 - точка максимума.
- точка максимума.
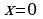 - точка минимума.
- точка минимума.
2) 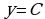 - прямая параллельная оси ОХ, проходящая через точку
- прямая параллельная оси ОХ, проходящая через точку 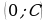 .
.
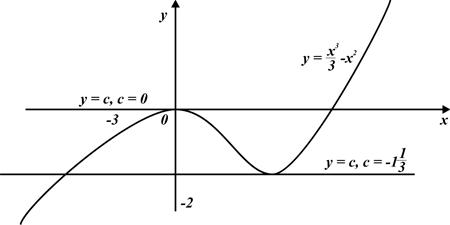
Изобразим схематично графики функций в одной координатной плоскости.
Н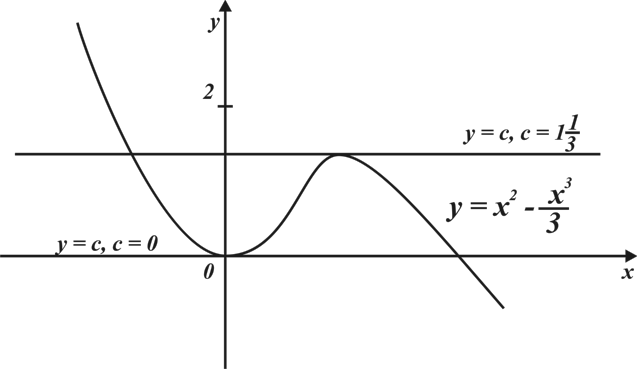 аглядно видно, что графики имеют две общие точки, если
аглядно видно, что графики имеют две общие точки, если 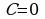 и
и 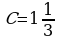 . Значит, графики первообразных
. Значит, графики первообразных 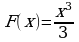 и
и 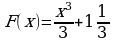 имеют ровно две общие точки с графиком функции
имеют ровно две общие точки с графиком функции 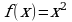 .
.
Ответ: 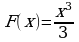 и
и 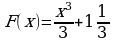 .
.
Вариант 2.
1) 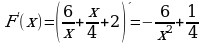 , то есть
, то есть 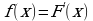 . Значит,
. Значит, 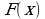 - первообразная для функции
- первообразная для функции 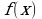 .
.
2) 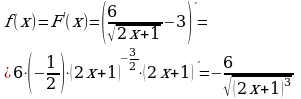
3) 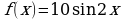
а) 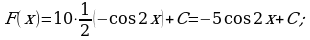
б) 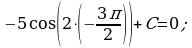
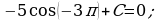
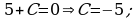
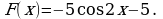
4)
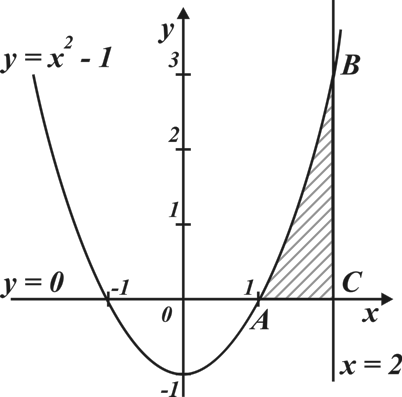
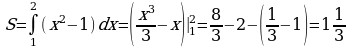
Ответ: 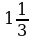 .
.
5) Общий вид первообразных 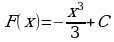 . Задача сводится к нахождению параметра С, когда уравнение
. Задача сводится к нахождению параметра С, когда уравнение 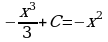 имеет два корня.
имеет два корня. 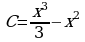
Рассмотрим функции 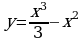 и
и 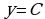 .
.
1) 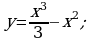
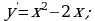
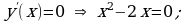
Критические точки: 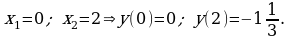
Определим знаки производной.
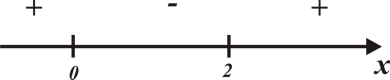
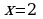 - точка минимума.
- точка минимума.
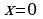 - точка максимума.
- точка максимума.
2) 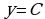 - прямая параллельная оси ОХ, проходящая через точку
- прямая параллельная оси ОХ, проходящая через точку 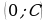 .
.
Изобразим схематично графики функций в одной координатной плоскости.
Наглядно видно, что графики имеют две общие точки, если 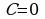 и
и 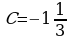 . Значит, графики первообразных
. Значит, графики первообразных 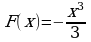 и
и 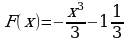 имеют ровно две общие точки с графиком функции
имеют ровно две общие точки с графиком функции 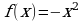 .
.
Ответ: 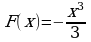 и
и 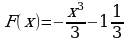 .
.
3. Итоги урока.
4. Домашнее задание.
Решить следующие задачи: стр. 205 №5(2).
Урок 21-22.
Зачет по теме «Первообразная и интеграл».
Цели урока: проверить уровень овладения учащимися изученного материала по данной теме, способствовать реализации полученных знаний при выполнении заданий различного уровня сложности, формировать у учащихся таких черт личности, как чувство взаимоответственности и самоутверждения, самоанализа и самооценки.
Основа урока взята из Интернета (урок учителя СШ№36 города Владимира Исаевой Ирины Михайловны).
Ход урока.
1. Организационный момент.
Урок – зачет проводится в форме игры. Класс делится на четыре команды, Выбирается капитан (до начала занятия). Команды садятся за свои столы. На столе каждой команды лежит «Лист учета знаний», где капитан напротив каждой фамилии ставит (в случае правильного ответа) знак «+».
По итогам каждого тура подсчитываются знаки «+» и в строке «всего» ставится их количество за команду. в строке напротив фамилии суммируются знаки «+» и можно выставить оценку каждому за работу на уроке.
Лист учета знаний.
| № | Фамилия Имя | Туры | Сумма плюсов | Оценка за урок. |
| 1 | 2 | 3 | 4 | 5 |
|
|
| 1 |
|
|
|
|
|
|
|
|
| 2 |
|
|
|
|
|
|
|
|
| 3 |
|
|
|
|
|
|
|
|
| 4 |
|
|
|
|
|
|
|
|
| 5 |
|
|
|
|
|
|
|
|
| 6 |
|
|
|
|
|
|
|
|
| 7 |
|
|
|
|
|
|
|
|
|
| Всего |
|
|
|
|
|
|
|
1 Тур «Разминка».
Отгадывание кроссворда. Здесь учащиеся должны показать свои теоретические знания на минимальном уровне. Кроссворд пишется на отдельных листах и выдается каждой команде. За каждое правильно угаданное слово команда получает 1 балл. Это задание на скорость, и команда, которая первая отгадала кроссворд, получает дополнительно 4 балла.
Максимальное количество баллов, которое может получить команда, равно 16.
Время выполнения задания 10 минут.
В листе учета знаний ставится в строке «Всего» число баллов, заработанных командой. Этот результат заносится в табло на доске.
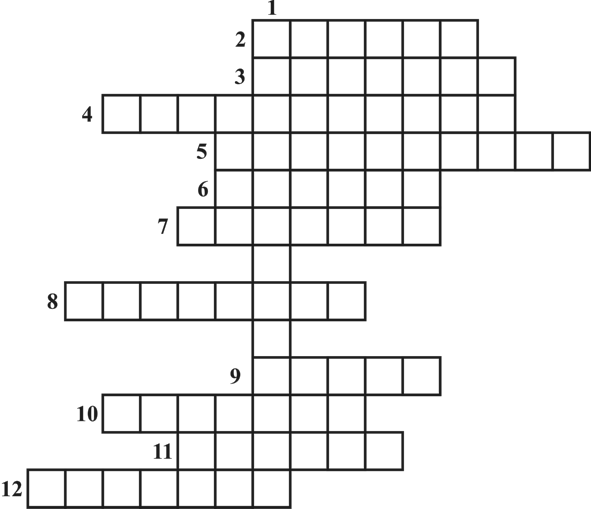
Как называется функция 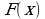 ?
?
Что является графиком функции 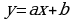 ?
?
Самая низкая школьная отметка?
Какой урок обычно проходит перед зачетом?
Синоним слова дюжина?
Есть в каждом слове, у растения и может быть у уравнения?
Что можно вычислить при помощи интеграла?
Одно из важнейших понятий математики.
Форма урока, на котором проводится проверка знаний.
Немецкий ученый, в честь которого названа формула, связывающая площадь криволинейной трапеции и интеграл.
Множество точек плоскости с координатами 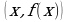 , где
, где 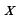 пробегает область определения функции
пробегает область определения функции 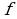 .
.
Соответствие между множествами 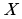 и
и 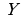 , при котором каждому значению множества
, при котором каждому значению множества  поставлено в соответствие единственное значение из множества
поставлено в соответствие единственное значение из множества  , носит название...
, носит название...
ОТВЕТЫ: 1. Первообразная. 2. Прямая. 3. Единица. 4. Контрольная. 5. Двенадцать. 6. Корень. 7. Площадь. 8. Интеграл. 9. Зачет. 10. Лейбниц. 11. График. 12. Функция.
2 Тур «Дальше, дальше…»
Этот гейм индивидуальный, то есть каждый учащийся пишет ответы в своей тетради. Время выполнения задания 15 минут. По окончании этого времени учитель зачитывает ответы. Учащиеся у себя в тетрадях обводят правильный ответ в кружок и подсчитывают количество кружков (столько плюсов ставят капитаны команд в «Лист учета знаний»), и каждый получает оценку за этот этап. Капитаны команд подсчитывают средний балл и сообщают преподавателю, который ставит эти данные в табло.
Что называется первообразной?
Как читается основное правило первообразной?
Как можно вычислить площадь криволинейной трапеции при помощи интеграла?
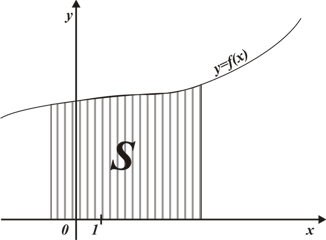
Запишите с помощью интеграл площадь фигуры изображенной на рисунке:
Найти первообразные для функций: а)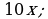 б)
б)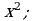 в)
в)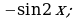 г)
г)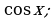 д)
д) 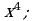 е)
е) 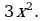
Истины ли равенства:
а) 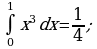 б)
б) 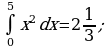 в)
в) 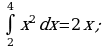
г) 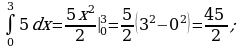
д) 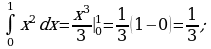
е) 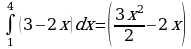 ?
?
ОТВЕТЫ:
1) Функция 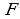 называется первообразной для функции
называется первообразной для функции 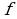 на заданном промежутке, если для всех
на заданном промежутке, если для всех 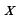 из этого промежутка
из этого промежутка 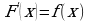 .
.
2) Любая первообразная для функции 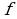 на промежутке может быть записана в виде
на промежутке может быть записана в виде 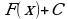 , где
, где 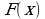 - одна из первообразных для функции
- одна из первообразных для функции 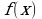 на заданном промежутке, а
на заданном промежутке, а 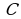 - произвольная постоянная.
- произвольная постоянная.
3) 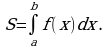
4) 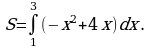
5) а) 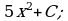 б)
б) 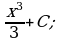 в)
в) 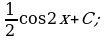 г)
г)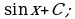 д)
д)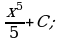 е)
е)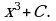
6) а) истинно; б) ложно; в) ложно; г) ложно; д) истинно; е) ложно.
3 Тур «Спешите видеть».
Каждая команда получает карточку с заданием. Первая и третья команды получают одинаковые карточки, вторая и четвертая тоже. Это задание на скорость и оно выполняется на отдельных листах. Время выполнения 10 минут. Команда, первая выполнившая задание, получает 1 дополнительный балл. За правильное выполнение задания команда получает 1 балл. В задании требуется изобразить криволинейную трапецию, ограниченную:
а) графиком функции 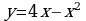 и прямой
и прямой 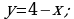
б) графиком функции 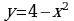 , осью ОХ и прямой
, осью ОХ и прямой 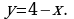
ОТВЕТЫ:
| а) | 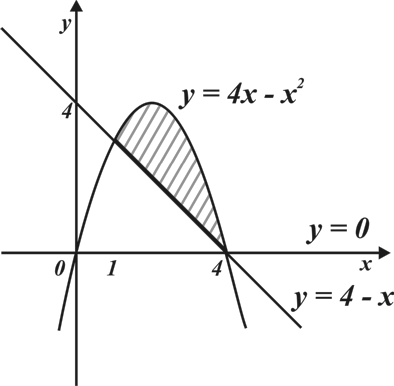
| б) | 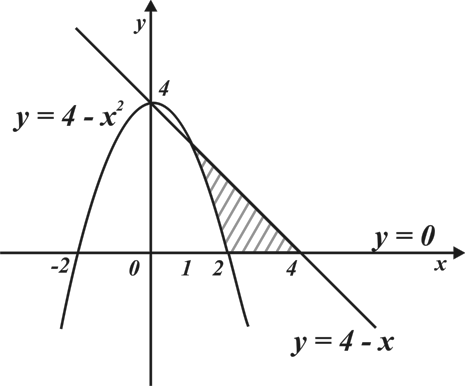
|
4 Тур «Составьте фразу».
Каждой команде выдается 7 карточек, на каждой из которых написано по 4 интеграл. Задача команды вычислить все 28 интегралов; найти на доске правильный ответ, под которым записана буква. Сопоставив результат вычисления интеграла и букву, учащиеся должны получить фразу. Команда, которая первая отгадает фразу, получает дополнительный балл. Балы начисляются команде за каждую правильно найденную букву. Время выполнения задания 20 минут.
Вычислить интегралы.
1) 
2) 
3) 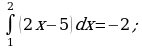
4) 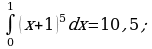
5) 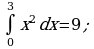
6) 
7) 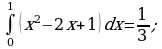
8) 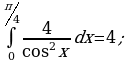
9) 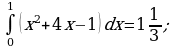
10) 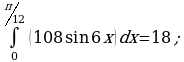
11) 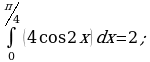
12) 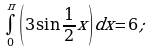
13) 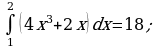
14) 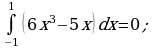
15) 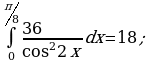
16) 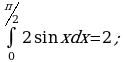
17) 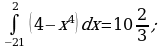
18) 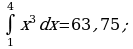
19) 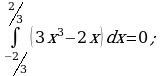
20) 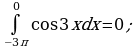
21) 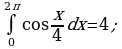
22) 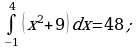
23) 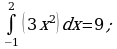
24) 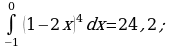
25) 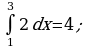
26) 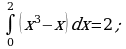
27) 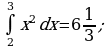
28) 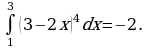
ОТВЕТЫ:
| В – 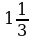 | А – 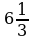 | Я – 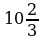 | Д – 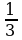 |
| Р – 2 | О – 4 | И – 6 | Ж – 6,2 |
| Т – 0 | З – (- 2) | Ь – 9 | Н – 10,5 |
| Е – 18 | К – 24,2 | Л – 48 | Ю – 63,75 |
В результате должно получиться:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| ж | и | з | н | ь | и | д | о | в | е | р | и | е | т |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| е | р | я | ю | т | т | о | л | ь | к | о | р | а | з |
5 Тур «Гонка за лидером».
Каждая команда получает карточку. Первая и третья команды получают карточку 1, вторая и четвертая команды получают карточку 2. В каждой карточке по два задания: одно в форме теста, другое – своеобразный кроссворд.
За первое правильно решенное задание команда получает 1 балл, за второе – 3 балла. Время выполнения задания 20 минут.
Карточка 1.
Задание 1.
Для функции 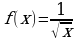 найти первообразную, график которой проходит через точку М(4; 5).
найти первообразную, график которой проходит через точку М(4; 5).
А)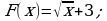 Б)
Б)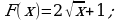
В)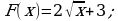 Г)
Г)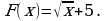
ОТВЕТ: Б.
Задание 2.
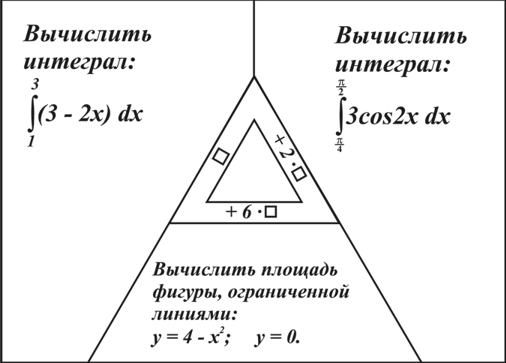
ОТВЕТ: 65.
Карточка 2.
Задание 1.
Для функции 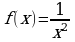 найти первообразную, график которой проходит через точку М(1; 3).
найти первообразную, график которой проходит через точку М(1; 3).
А)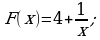 Б)
Б) 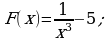
В) 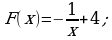 Г)
Г)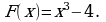
ОТВЕТ: В.
Задание 2.
ОТВЕТ: 28.
Подведение итогов
На табло подсчитываются баллы, полученные каждой командой, и распределяются места. Каждый участник команды занявшей 1 место получает оценку «5». Кроме этого, все учащиеся получают оценку за индивидуальное задание и за работу в коллективе.
Каждая команда должна ответить на следующие вопросы:
1. Что вам понравилось в зачете такого рода?
2. Какие цели были достигнуты на этом уроке?
3. Что вам не понравилось и что бы вы изменили?
Вместо урока – зачета можно провести тест по вариантам.
Вариант 1.
Вычислите 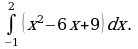
а) 27; б) 24; в) 18; г) 21.
Найдите 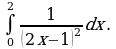
а) 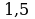 ; б)
; б) 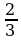 ; в)
; в) 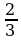 ; г) интеграл не существует.
; г) интеграл не существует.
Вычислите 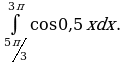
а) - 2; б) 2; в) - 3; г) 3.
Вычислите 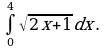
а) 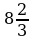 ; б)
; б) 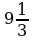 ; в)
; в) 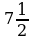 ; г)
; г) 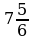 .
.
При каком значении 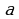 выполняется равенство
выполняется равенство 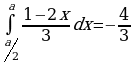 ?
?
а) 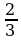 ; б)
; б) 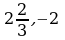 ; в)
; в) 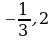 ; г)
; г) 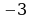 .
.
Вычислите площадь фигуры, ограниченной графиком функции 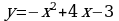 и прямой
и прямой 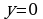
а) 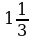 ; б)
; б) 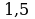 ; в)
; в) 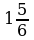 ; г)
; г) 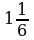 .
.
Вычислите площадь фигуры, ограниченной графиком функции 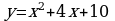 , касательной к параболе в точке
, касательной к параболе в точке 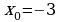 и прямой
и прямой 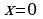
а) 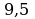 ; б)
; б) 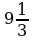 ; в)
; в) 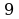 ; г)
; г) 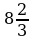 .
.
Вычислите площадь фигуры, ограниченной графиками функций 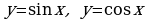 и прямыми
и прямыми 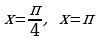 .
.
а) 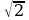 ; б)
; б) 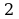 ; в)
; в) 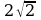 ; г)
; г) 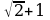 .
.
Найдите 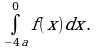
а) 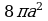 ; б)
; б) 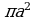 ; в)
; в) 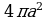 ; г)
; г) 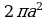 .
.
График функции 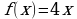 пересекает график своей первообразной
пересекает график своей первообразной 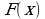 в двух точках, одна из которых (-1;-4). Найдите площадь фигуры, ограниченной графиками
в двух точках, одна из которых (-1;-4). Найдите площадь фигуры, ограниченной графиками 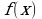 и
и 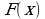 .
.
а) 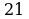 ; б)
; б) 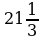 ; в)
; в) 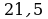 ; г)
; г) 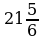 .
.
Вариант 2.
Вычислите 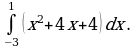
а) 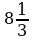 ; б)
; б) 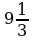 ; в)
; в) 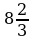 ; г)
; г) 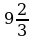 .
.
Найдите 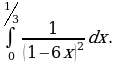
а) 0; б) -12; в) интеграл не существует; г) 12.
Вычислите 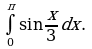
а) – 3,5; б) 4,5; в) – 4,5; г) 3,5.
Вычислите 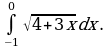
а) 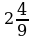 ; б)
; б) 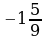 ; в)
; в) 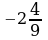 ; г)
; г) 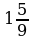 .
.
При каком значении 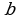 выполняется равенство
выполняется равенство 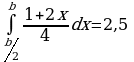 ?
?
а) 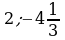 ; б)
; б) 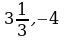 ; в)
; в) 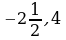 ; г)
; г) 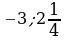 .
.
Вычислите площадь фигуры, ограниченной графиком функции 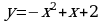 и прямой
и прямой 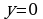
а) 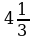 ; б)
; б) 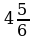 ; в)
; в) 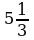 ; г)
; г) 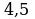 .
.
Вычислите площадь фигуры, ограниченной графиком функции 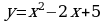 , касательной к параболе в точке
, касательной к параболе в точке 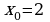 и прямой
и прямой 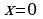
а) 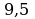 ; б)
; б) 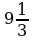 ; в)
; в) 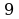 ; г)
; г) 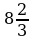 .
.
Вычислите площадь фигуры, ограниченной графиками функций 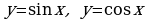 и прямыми
и прямыми 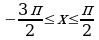 .
.
а) 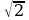 ; б)
; б) 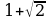 ; в)
; в) 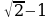 ; г)
; г) 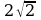 .
.
Найдите 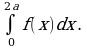
а) 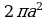 ; б)
; б) 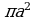 ; в)
; в) 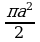 ; г)
; г) 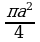 .
.
График функции 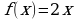 пересекает график своей первообразной
пересекает график своей первообразной 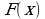 в двух точках, одна из которых (3;6). Найдите площадь фигуры, ограниченной графиками
в двух точках, одна из которых (3;6). Найдите площадь фигуры, ограниченной графиками 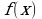 и
и 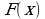 .
.
а) 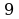 ; б)
; б) 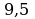 ; в)
; в) 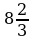 ; г)
; г) 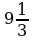 .
.
ОТВЕТЫ:
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | Г | Г | В | А | Б | А | В | Г | Г | Б |
| 2 | Б | В | В | Г | Б | Г | А | Б | В | А |







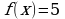
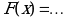
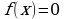
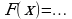
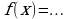
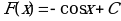
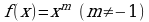
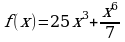
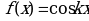
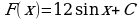
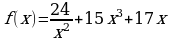
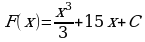
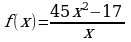
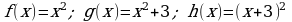

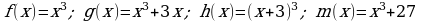
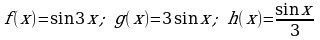
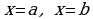 , ось OX, учащиеся выявят особенности фигуры, которая называется криволинейной трапецией. Рассмотреть пример. Вычислить площадь криволинейной трапеции, ограниченной графиком функции
, ось OX, учащиеся выявят особенности фигуры, которая называется криволинейной трапецией. Рассмотреть пример. Вычислить площадь криволинейной трапеции, ограниченной графиком функции 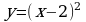 , прямыми
, прямыми 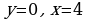 и
и 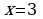 . Решая это простое задание напомнить учащимся, что данную параболу можно строить двумя способами:
. Решая это простое задание напомнить учащимся, что данную параболу можно строить двумя способами: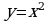 , смещая его вдоль оси OX на две единицы вправо.
, смещая его вдоль оси OX на две единицы вправо.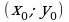 по формуле , затем находя несколько контрольных точек.
по формуле , затем находя несколько контрольных точек.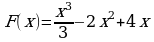 .
. 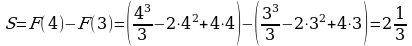 .
.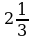
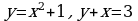 .
.
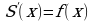



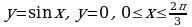 , используя формулу
, используя формулу 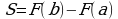 .
.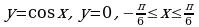 , используя формулу
, используя формулу 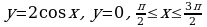 , используя формулу
, используя формулу 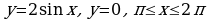 , используя формулу
, используя формулу 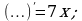 б)
б) 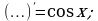 в)
в) 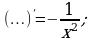
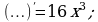 д)
д) 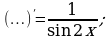 е)
е) 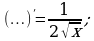
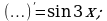 з)
з) 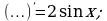 и)
и) 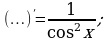


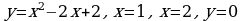
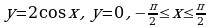
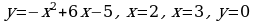
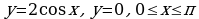
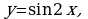 если
если 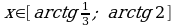
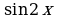 для значений на концах отрезка области определения.
для значений на концах отрезка области определения.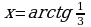 , то
, то 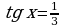 ,
, 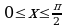 , т.е.
, т.е.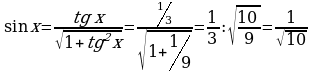
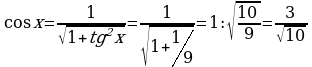
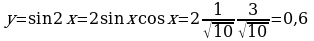
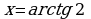 , то
, то 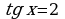 ,
, 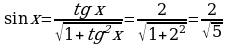
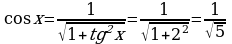
 .
.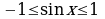 . Максимум функции
. Максимум функции 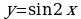 принадлежит данному отрезку
принадлежит данному отрезку 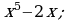 б)
б) 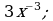 в)
в) 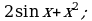
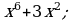 д)
д) 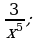 е)
е) 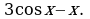
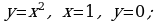
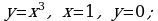
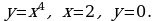
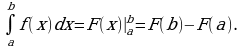
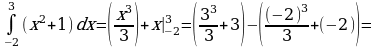
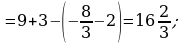
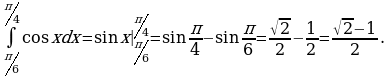
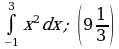
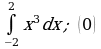
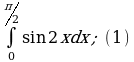
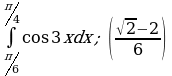
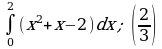
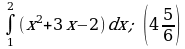
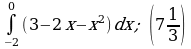
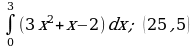
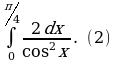
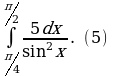
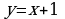 и параболой
и параболой 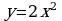 .
.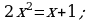
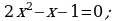
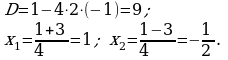

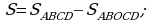
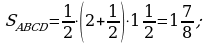
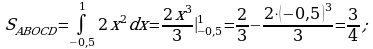
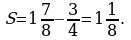
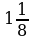 .
.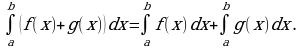
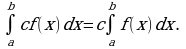
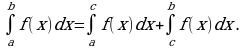
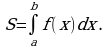
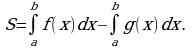
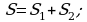
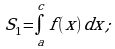
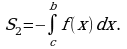
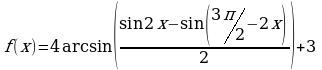
 , получим
, получим 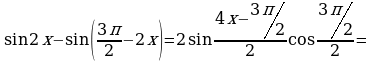
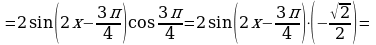
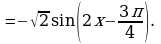
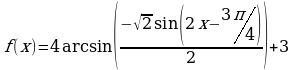 . Множество значений функции
. Множество значений функции 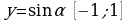 . Используем запись двойного неравенства для записи множества значений.
. Используем запись двойного неравенства для записи множества значений.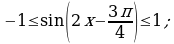
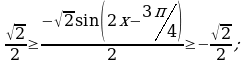
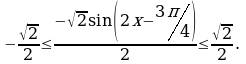
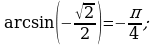
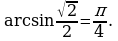
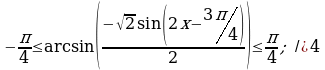
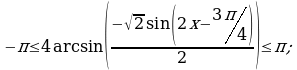
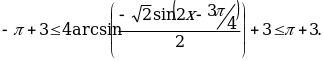
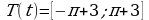 . Удалим целые числа из множества значений и посчитаем количество числовых промежутков, используем для этого координатную прямую.
. Удалим целые числа из множества значений и посчитаем количество числовых промежутков, используем для этого координатную прямую.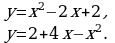
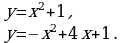
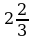 .
.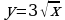 и
и 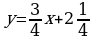 .
.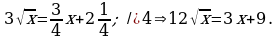
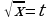 , тогда
, тогда 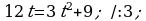
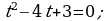
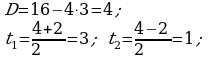
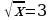 , то
, то 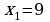 .
.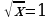 , то
, то 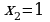 .
.
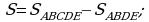
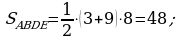
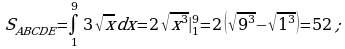
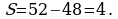
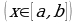 поставлено в соответствии единственное число
поставлено в соответствии единственное число 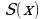 - площадь сечения тела этой плоскостью. Имеется функция
- площадь сечения тела этой плоскостью. Имеется функция 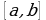 .
.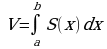 .
.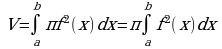 .
. ействительно, каждая плоскость, перпендикулярная оси ОХ и пересекающая отрезок
ействительно, каждая плоскость, перпендикулярная оси ОХ и пересекающая отрезок 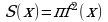 .
.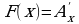
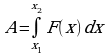
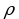 - линейная плотность;
- линейная плотность;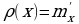
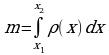
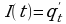
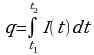
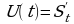
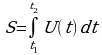
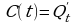
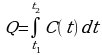
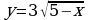 и
и 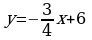 .
. айдем абсциссы точек пересечения графиков.
айдем абсциссы точек пересечения графиков.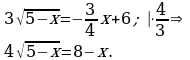
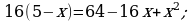
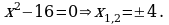
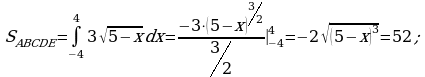
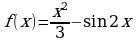 на промежутке
на промежутке 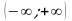 .
.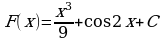 ; 2)
; 2) 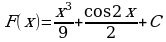 ;
;  ; 4)
; 4) 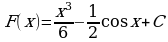 .
.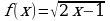 на промежутке
на промежутке 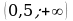 .
.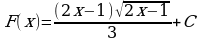 ;
; 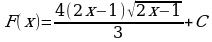 ;
; 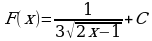 ;
; 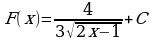 .
.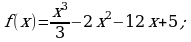 б)
б) 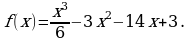
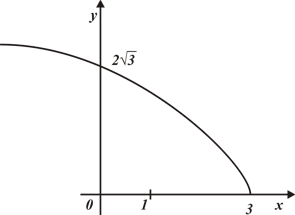
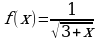 . Укажите график функции
. Укажите график функции 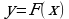 , если
, если 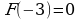 .
.
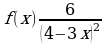 найдите ее первообразную, если
найдите ее первообразную, если 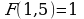 .
.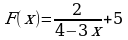 .
.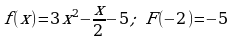 , найдите
, найдите 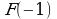 .
.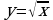 .
.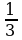 .
.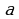 . уравнение
. уравнение 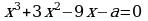 имеет ровно два корня?
имеет ровно два корня?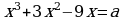 . Найдем решение графическим способом. Построим в одной системе координат графики функций
. Найдем решение графическим способом. Построим в одной системе координат графики функций 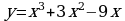 и
и 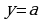 .
.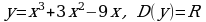
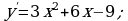
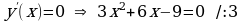
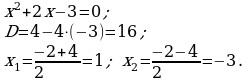
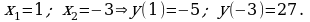
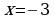 - точка максимума.
- точка максимума.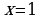 - точка минимума.
- точка минимума.
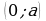 .
.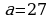 или
или 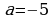 .
.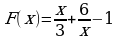 есть первообразная для функции
есть первообразная для функции 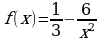 на промежутке
на промежутке 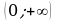 .
.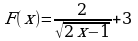 есть первообразная для функции f(x) на промежутке
есть первообразная для функции f(x) на промежутке 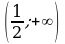 . Найти f(x).
. Найти f(x).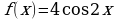 найдите:
найдите: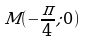 .
.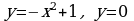 .
.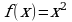 , графики которых имеют ровно две общие точки с графиком функции
, графики которых имеют ровно две общие точки с графиком функции 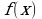 .
.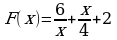 есть первообразная для функции
есть первообразная для функции 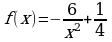 на промежутке
на промежутке 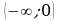 .
.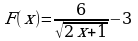 есть первообразная для функции f(x) на промежутке
есть первообразная для функции f(x) на промежутке 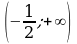 . Найти f(x).
. Найти f(x).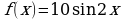 найдите:
найдите: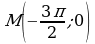 .
.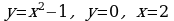 .
.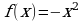 , графики которых имеют ровно две общие точки с графиком функции
, графики которых имеют ровно две общие точки с графиком функции 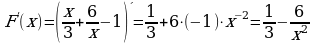 , то есть
, то есть 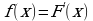 . Значит,
. Значит, 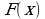 - первообразная для функции
- первообразная для функции 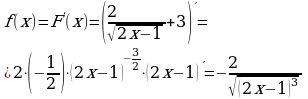
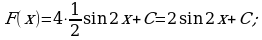
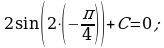
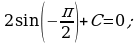
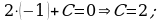
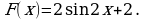

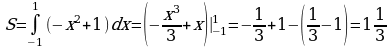
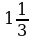 .
.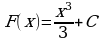 . Задача сводится к нахождению параметра С, когда уравнение
. Задача сводится к нахождению параметра С, когда уравнение 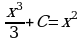 имеет два корня.
имеет два корня. 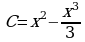
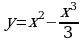 и
и 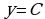 .
.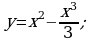
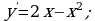
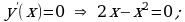
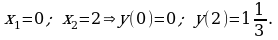
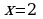 - точка максимума.
- точка максимума.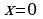 - точка минимума.
- точка минимума.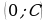 .
. аглядно видно, что графики имеют две общие точки, если
аглядно видно, что графики имеют две общие точки, если 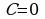 и
и 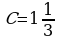 . Значит, графики первообразных
. Значит, графики первообразных 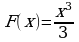 и
и 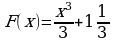 имеют ровно две общие точки с графиком функции
имеют ровно две общие точки с графиком функции 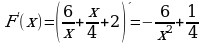 , то есть
, то есть 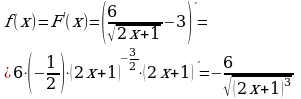
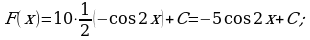
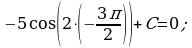
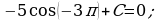
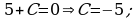
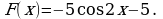

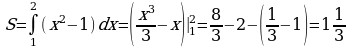
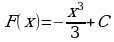 . Задача сводится к нахождению параметра С, когда уравнение
. Задача сводится к нахождению параметра С, когда уравнение 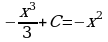 имеет два корня.
имеет два корня. 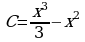
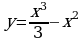 и
и 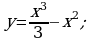
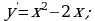
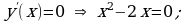
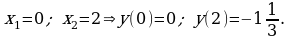

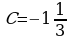 . Значит, графики первообразных
. Значит, графики первообразных 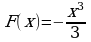 и
и 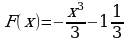 имеют ровно две общие точки с графиком функции
имеют ровно две общие точки с графиком функции 
 ?
? , где
, где 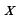 пробегает область определения функции
пробегает область определения функции 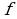 .
.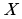 и
и 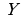 , при котором каждому значению множества
, при котором каждому значению множества 
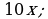 б)
б)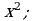 в)
в)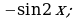 г)
г)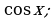 д)
д) 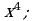 е)
е) 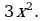
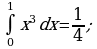 б)
б) 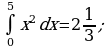 в)
в) 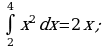
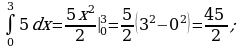
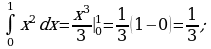
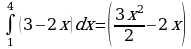 ?
?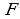 называется первообразной для функции
называется первообразной для функции 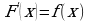 .
.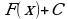 , где
, где 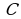 - произвольная постоянная.
- произвольная постоянная.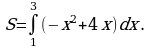
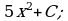 б)
б) 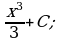 в)
в) 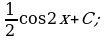 г)
г)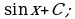 д)
д)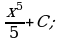 е)
е)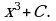
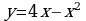 и прямой
и прямой 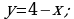
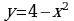 , осью ОХ и прямой
, осью ОХ и прямой 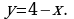


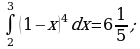
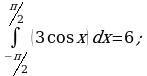
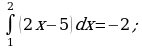
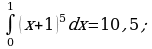
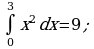

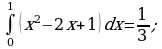
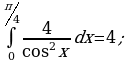
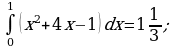
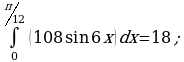
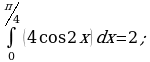
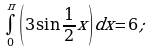
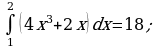
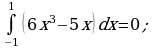
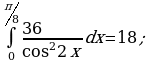
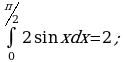
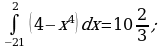
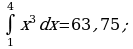
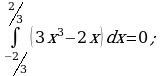
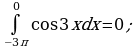
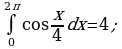
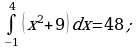
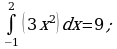
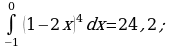
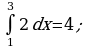
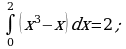
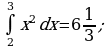
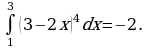
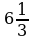
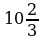
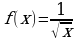 найти первообразную, график которой проходит через точку М(4; 5).
найти первообразную, график которой проходит через точку М(4; 5).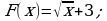 Б)
Б)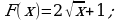
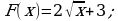 Г)
Г)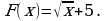

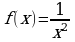 найти первообразную, график которой проходит через точку М(1; 3).
найти первообразную, график которой проходит через точку М(1; 3).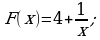 Б)
Б) 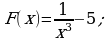
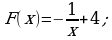 Г)
Г)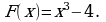

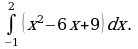
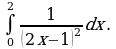
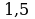 ; б)
; б) 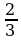 ; в)
; в) 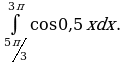
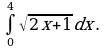
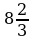 ; б)
; б) 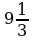 ; в)
; в) 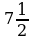 ; г)
; г) 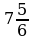 .
.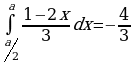 ?
?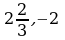 ; в)
; в) 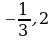 ; г)
; г) 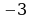 .
.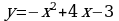 и прямой
и прямой 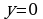
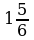 ; г)
; г) 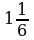 .
.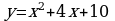 , касательной к параболе в точке
, касательной к параболе в точке 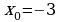 и прямой
и прямой 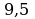 ; б)
; б) 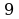 ; г)
; г) 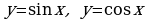 и прямыми
и прямыми 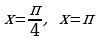 .
.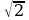 ; б)
; б) 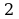 ; в)
; в) 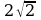 ; г)
; г) 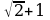 .
.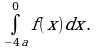

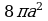 ; б)
; б) 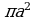 ; в)
; в) 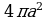 ; г)
; г) 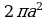 .
.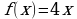 пересекает график своей первообразной
пересекает график своей первообразной 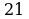 ; б)
; б) 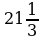 ; в)
; в) 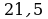 ; г)
; г) 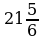 .
.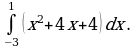
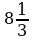 ; б)
; б) 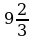 .
.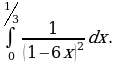
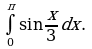
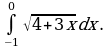
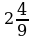 ; б)
; б) 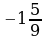 ; в)
; в) 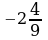 ; г)
; г) 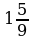 .
.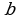 выполняется равенство
выполняется равенство 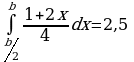 ?
?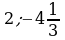 ; б)
; б) 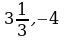 ; в)
; в) 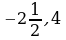 ; г)
; г) 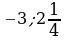 .
.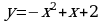 и прямой
и прямой 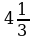 ; б)
; б) 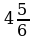 ; в)
; в) 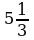 ; г)
; г) 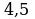 .
.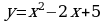 , касательной к параболе в точке
, касательной к параболе в точке 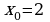 и прямой
и прямой 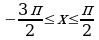 .
.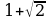 ; в)
; в) 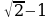 ; г)
; г) 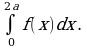

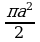 ; г)
; г) 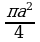 .
.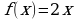 пересекает график своей первообразной
пересекает график своей первообразной 









