Просмотр содержимого документа
«Повторение 9 класс. Тектовые задачи + прогрессии»
Текстовые задачи
Через одну трубу бассейн наполняется за 4 часа, через вторую – за 3 часа. Сколько времени нужно, чтобы наполнить бассейн на 70%, если открыть обе трубы одновременно?
А) 2 часа B) 1,5 часа C) 1,2 часа D) 1 час E) 1,8 часа
Двое рабочих, работая совместно с одинаковой производительностью, могут выполнить заказ за 5,5 часа. За сколько времени они выполнят заказ, если один из рабочих увеличит свою производительность на 20%?
А) 3,5 часа B) 3 часа C) 4,5 часа D) 4 часа E) 5 часов
Два трактора, работая вместе, могут вспахать поле за 6 часов. Первый трактор, работая отдельно, может вспахать это поле на 5 часов быстрее, чем второй. За сколько часов первый трактор, работая отдельно, может вспахать поле?
А) 4 часа B) 9 часов C) 5 часов D) 10 часов E) 6 часов
Фермер планировал закончить сев за 12 дней. Увеличив норму посева на 2 га в день, он закончил сев за 8 дней. Сколько гектаров фермер засевал ежедневно?
А) 7 B) 8 C) 5 D) 4 E) 6
В первую попытку экзамен по математике сдали 60% студентов 1 курса, а вторично – 40% оставшихся студентов. Сколько процентов студентов сдали экзамен за эти две попытки?
А) 88 B) 92 C) 84 D) 76 E) 80
Объем продукции на предприятии за январь вырос на 40%, а за февраль уменьшился на 50%. На сколько процентов уменьшился объем продукции на предприятии за эти два месяца?
А) 10 B) 20 C) 30 D) 40 E) 70
Сумма чисел А, В и С равна 19. Треть числа В в два раза меньше С, а если увеличить А на 20%, то получится 80% числа С. Найдите произведение чисел А, В и С.
А) 216 B) 225 C) 240 D) 245 E) 252
Когда бочка пуста на 30%, она содержит на 30 литров меда больше, чем когда она полна на 30%. Сколько литров меда в полной бочке?
А) 60 B) 75 C) 90 D) 100 E) 120
В каком отношении нужно брать 10%-ный и 20%-ный растворы соли, чтобы при их смешивании получился 16%-ный раствор?
А) 1:1 B) 1:2 C) 2:3 D) 3:4 E) 3:5
В 4 кг 12-ти процентного раствора соли добавили 2 кг воды. Каково процентное содержание соли в полученном растворе?
А) 2% B) 3% C) 6% D) 8% E) 9%
Содержание сахара в одном соке – 10%, а в другом – 15%. Смешали 2 л первого и 3 л второго сока. Каково содержание сахара в смеси?
А) 5% B) 12,5% C) 12,755% D) 13% E) 25%
Кусок сплава меди и серебра массой в 36 кг содержит 45% меди. Какую массу меди нужно добавить к этому куску, чтобы полученный сплав содержал 60% меди?
А) 12,5 B) 13,5 C) 14,5 D) 15,5 E) 16,5
В банке с компотом плавают сливы и абрикосы. Сливы составляют 40% всех фруктов. Вася выловил из банки несколько слив и съел их. Теперь оставшиеся сливы составили 20% всех фруктов в банке. Сколько процентов всех слив съел Вася?
А) 20% B) 62,5% C) 50% D) 60% E) другой ответ
Автобус из А в В ехал со скоростью 45 км в час, а из В в А – со скоростью 55 км в час. Какова средняя скорость автобуса?
А) 40 B) 48 C) 49,5 D) 50 E) 60
Из А в В по течению реки катер добирается в два раза быстрее, чем из В в А. Во сколько раз скорость катера больше скорости течения реки?
А) 1,5 B) 2 C) 2,5 D) 3 E) 4
Турист проплыл на лодке против течения реки 6 км и 15 км – по озеру, затратив на путь по озеру на 1 час меньше, чем на путь по реке. Найти скорость лодки туриста в стоячей воде, если скорость течения реки равна 2 км/ч.
А) 1 B) 2 C) 3 D) 4 E) 5
Скорость первого автомобиля относится к скорости второго как 7:8. Автомобили одновременно выезжают навстречу друг другу из двух городов, расстояние между которыми равно 465 км, и встречаются через 4 часа. Найдите скорость второго автомобиля.
А) 60 B) 62 C) 64 D) 66 E) 68
Расстояние между двумя речными причалами 90 км. Теплоход на весь рейс туда и обратно затрачивает 7,5 ч. Найдите скорость теплохода в стоячей воде, если скорость течения реки составляет 20% от скорости теплохода.
А) 15 B) 20 C) 25 D) 30 E) 35
За 30 минут катер проходит по течению реки такое же расстояние, какое за 40 минут – против течения, причем 2 км против течения он проходит за 10 минут. Собственная скорость катера
(в км/ч) равна
А) 11 B) 12 C) 13 D) 14 E) 15
Скорость шлюпки при движении по реке против течения составляет  от скорости шлюпки по течению. На сколько процентов скорость течения меньше скорости шлюпки в стоячей воде?
от скорости шлюпки по течению. На сколько процентов скорость течения меньше скорости шлюпки в стоячей воде?
Доля брака в партии изделий составляла 9%. На стадии контроля качества удалось выявить и изъять из партии 40 бракованных изделий. Сколько изделий осталось в партии, если доля брака в ней составляет теперь 2,5%?
К какому количеству (в граммах) раствора соли четырехпроцентной концентрации надо добавить 25 г раствора соли девятипроцентной концентрации, чтобы получить пятипроцентный раствор соли?
Из сосуда, доверху наполненного 91%–м раствором кислоты, отлили 2 литра жидкости и долили 2 литра 55%–го раствора этой же кислоты. После этого в сосуде получился 79%–й раствор кислоты. Сколько литров раствора вмещает сосуд?
На баржу было погружено 810 тонн песка, влажность которого составляла 15%. Во время перевозки из пункта А в пункт В влажность песка повысилась на 4%. Найдите массу груза, доставленного в пункт В.
Для отправки груза было подано несколько вагонов. Если грузить по 13,4 т в вагон, то 5 т груза останутся непогруженными, если грузить по 14,4 т, то для полной загрузки не хватит 10 т груза. Сколько было груза (в тоннах)?
Том Сойер может окрасить половину забора за 4 часа 30 мин. На сколько процентов производительность работы Гекльбери Финна выше, если две трети забора он окрасит за 2 часа?
Том Сойер собирал скелеты дохлых кошек, а Гекльбери Финн ловил летучих мышей. Друзья посчитали свою добычу, после чего отправились на новые поиски. Том Сойер увеличил свою добычу на 80%, а Гекльбери Финн – на 40%. В итоге общее число трофеев возросло в полтора раза. Сколько процентов от общего числа трофеев в первоначальной коллекции составляли летучие мыши?
Два маляра, работая вместе, могут за 1 ч покрасить стену площадью 40 м². Первый маляр, работая отдельно, может покрасить 50 м² на 4 ч быстрее, чем второй покрасит 90 м² такой же стены. За сколько времени первый маляр может покрасить 100 м² стены?
Задачи на прогрессии
Произведение первых семи членов геометрической прогрессии, у которой четвертый член равен 3, равно
А) 9 B) 81 C) 21 D)  E)
E) 
Если в геометрической прогрессии знаменатель равен –2, а сумма первых пяти членов равна 5,5, то ее первый член равен
А) –0,5 B) 1,5 C) 0,5 D) –1 E) –1,5
В геометрической прогрессии первый член равен 3, а шестой член равен 96. Найдите сумму первых восьми членов прогрессии.
А) 381 B) 512 C) 688 D) 765 E) 1533
В возрастающей геометрической прогрессии пятый член равен 18, а сумма четвертого и шестого членов равна 60. Найдите сумму третьего и шестого членов прогрессии
А) 52 B) 56 C) 60 D) 64 E) 168
В геометрической прогрессии сумма второго и пятого членов равна 36, а разность пятого и второго членов равна 28. Найдите сумму первых пяти членов прогрессии
А) 32 B) 62 C) 76 D) 40 E) 48
Дана геометрическая прогрессия, в которой сумма первых трех членов равна 14, а сумма первых шести членов равна –– 126. Найдите второй член прогрессии.
А) –4 B) 4 C) 0 D) 0,5 E) 
Если сумма бесконечно убывающей геометрической прогрессии равна 32, а сумма ее первых пяти членов равна 31, то первый член прогрессии равен
А) 16 B) 18 C) 12 D) 8 E) 24
Найдите отношение пятого члена арифметической прогрессии к первому, если второй член прогрессии равен 3, а шестой равен 11.
А) 4 B) –5 C) 7 D) 9 E) –4
В арифметической прогрессии сумма второго и десятого членов равна 20, а сумма пятого и девятого членов равна 16. Найдите сумму первых четырнадцати членов прогрессии.
А) 46 B) 70 C) 98 D) 112 E) 126
В арифметической прогрессии, все члены которой положительны, сумма первого и пятого членов равна 10, а произведение второго и четвертого –– 21. Чему равна сумма первых четырех членов прогрессии?
А) 16 B) 120 C) 20 D) 32 E) 36
Сумма трех чисел, образующих арифметическую прогрессию, равна 111. Второе число больше первого в 5 раз. Найдите первое число.
А) 5,6 B) 4,7 C) 6 D) 6,5 E) 7,4
В арифметической прогрессии c разностью 4 первый член равен 3. Какое наименьшее количество (первых) членов прогрессии надо взять, чтобы сумма этих членов была больше 1000?
А) 22 B) 23 C) 24 D) 25 E) 26
В арифметической прогрессии сумма седьмого, восьмого и пятнадцатого членов равна 42. Чему равна сумма девятого и одиннадцатого членов прогрессии?
А) 28 B) 29 C) 30 D) 31 E) 100
Сумма всех двузначных чисел, делящихся на 3, равна
А) 1400 B) 1600 C) 1507 D) 1665 E) 1502
В арифметической прогрессии шестой член равен 10, а сумма второго и восьмого членов равна 12. Вычислите сумму первых двенадцати членов прогрессии.
В арифметической прогрессии сумма первых трех членов равна 30, разность шестого и четвертого членов равна –4, а n–член равен –10. Найдите n.
В арифметической прогрессии известны члены  и
и  . Укажите номер k члена этой прогрессии, начиная с которого все ее члены неположительны.
. Укажите номер k члена этой прогрессии, начиная с которого все ее члены неположительны.
В геометрической прогрессии известны члены  и
и 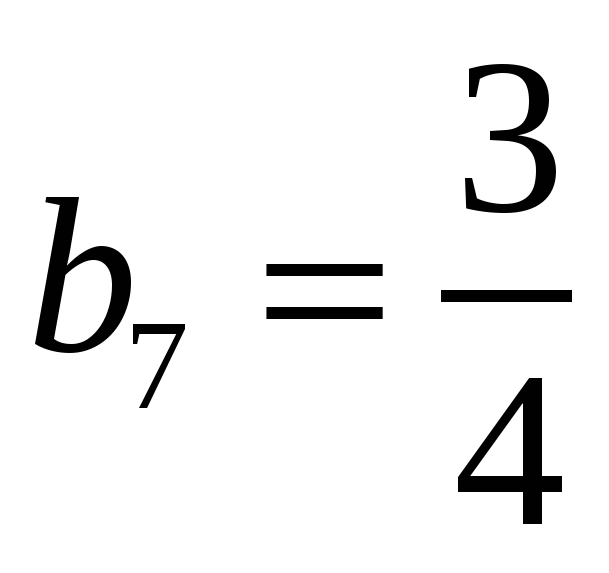 . Укажите номер k члена этой прогрессии, начиная с которого все ее члены больше 768.
. Укажите номер k члена этой прогрессии, начиная с которого все ее члены больше 768.
Найдите наибольшую из сумм первых n членов арифметической прогрессии, если  и
и  .
.
В арифметической прогрессии  ,
,  . Укажите такое значение n, при котором сумма
. Укажите такое значение n, при котором сумма  принимает наименьшее возможное значение.
принимает наименьшее возможное значение.
Найдите сумму всех нечетных k, каждое из которых делится без остатка на 7 и удовлетворяет условию 
За 10 дней Карл украл у Клары 165 кораллов и из них 147 – в первые 7 дней. Каждый день он крал на одно и то же число кораллов меньше, чем в предыдущий день. Сколько кораллов Карл украл в десятый день?
В знакочередующейся геометрической прогрессии первый член равен 7, а сумма третьего и пятого членов равна 630. Найдите второй член прогрессии.
Если к четырем числам А, В, С, D, составляющим геометрическую прогрессию, прибавить соответственно 35, 57, 59 и 1, то получатся четыре числа, составляющие арифметическую прогрессию. Найдите сумму чисел А, В, С, D.
Если к четырем числам А, В, С, D, составляющим арифметическую прогрессию, прибавить соответственно 3, 5, 15 и 41, то получатся четыре числа, составляющие геометрическую прогрессию. Найдите сумму чисел А, В, С, D.
Найдите сумму значений t или значение t, если оно единственное, при котором числа –3; t+1; 2t–7 являются тремя последовательными членами убывающей геометрической прогрессии.
Найдите сумму значений х или значение х, если оно единственное, при котором положительные числа 2х–2; 4х+5;  являются тремя последовательными членами арифметической прогрессии.
являются тремя последовательными членами арифметической прогрессии.
Ответы «Текстовые задачи»
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| C | E | D | E | D | C | A | B | C | D | D | B | B | C | D | C | B | C | D | 72 | 560 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 100 | 6 | 850 | 206 | 200 | 75 | 4 |
Ответы «Прогрессии»
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| E | C | D | B | B | B | A | D | C | A | E | B | A | D | 144 | 12 | 27 | 18 | 685 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 21 | 945 | 3 | – 21 | 200 | 56 | – 10 | 8 |

















