Конспект повторительно-обобщающего урока по алгебре в 9 классе
Учитель: Тырина Ю.В.
Тема. Решение уравнений.
Типология урока:
- по основной дидактической цели: урок обобщения и систематизации знаний;
- по основным этапам учебного процесса: комбинированный;
- по форме проведения: нетрадиционный - путешествие во времени.
Цели урока:
Обобщить и систематизировать знания учащихся по теме «Решение уравнений с одной переменной» по всему курсу основной средней школы.
Совершенствовать навык решения уравнений с одной переменной.
Продолжить формирование умений решать уравнения, используя введение новой переменной (заменой).
Познакомить с некоторыми способами решения иррациональных уравнений.
Материально-техническое обеспечение урока:
компьютер;
проектор;
презентация
ХОД УРОКА.
Мотивационный этап.
- Организационный момент: приветствие и подготовка к уроку.
- Мотивация.
-Рефлексия.
Учитель: Ребята, а вы знаете что-нибудь о происхождении слова «алгебра»? (Слайд 1)
Ученики: Нет.
Учитель: Для вас уже не секрет, что алгебра – один из важнейших разделов математики. Алгебра, как наука, складывалась в недрах арифметики, от которой она долгое время не отделялась. В истории арифметики и алгебры большое значение имеют труды Мухаммеда Ал-Хорезми. (Слайд 2). Написанный им в начале IX в., трактат «Китаб ал-джабр ва-л-мукабала» явился первым в мире самостоятельным сочинением по алгебре. Это название связано с двумя приемами решения уравнений:
Данный трактат был переведен в XII веке на латинский язык. Он стал тем сочинением, оттолкнувшись от которого пошло дальнейшее развитие алгебры, но уже на Европейской почве. Переводчики сочинения бен-Муса постепенно отбросили вторую часть названия его трактата, оставив только первую – аль-джебр, или, как мы теперь говорим, алгебра. Мухаммед Ал-Хорезми утверждал, что алгебра- «это искусство решения уравнений, необходимое людям в случаях наследования, наследственных пошлин, раздела имущества, торговли и во всех их деловых взаимоотношениях или же в случае измерения земель, проведения каналов, геометрических вычислений и других предметов различного рода…».
Уравнения в школьном курсе алгебры занимают ведущее место. На их изучение отводится времени больше, чем на любую другую тему. Действительно, уравнения не только имеют важное теоретическое значение, но и служат чисто практическим целям. Подавляющее большинство задач о пространственных формах и количественных отношениях реального мира сводится к решению различных видов уравнений. Овладевая способами их решения, мы находим ответы на различные вопросы из науки и техники (транспорт, сельское хозяйство, промышленность, связь и т. д.). Уравнения с давних времен волновали умы человечества. (Слайд 4). Послушайте, какие прекрасные слова посвящены уравнениям:
Сухие строки уравнений –
В них сила разума влилась.
В них объяснение явлений,
Вещей разгаданная связь.
Посредством уравнений, теорем
он уйму всяких разрешил проблем:
и засуху предсказывал, и ливни.
Поистине его познанья дивны.
Учитель: И сегодня наш урок мы посвящаем решению уравнений. (Слайд 5).
Открываем тетради, записываем число и тему урока. Так как уравнения вы решаете не первый год, будем изучать различные виды уравнений и в 10-11 классе, я хочу вам предложить сегодня попутешествовать во времени, т.е. побывать в прошлом, настоящем и заглянуть в будущее.
Ну а вначале я хотела бы посмотреть, а стоит ли вообще начинать наше путешествие.
« Человек не может понимать окружающий его мир только логикой мозга, он должен ощутить его логикой сердца, то есть эмоцией».
Когда вы слышите слово уравнение, читаете задание решить уравнение, какие чувства и эмоции вы испытываете? (смайлы)
Как вы думаете, что нам необходимо, чтобы путешествовать во времени?
Ученики: Машина времени. (Слайд 6).
Учитель: А что для нас сегодня на уроке будет машиной времени, которая позволит нам, переносится из прошлого в настоящее и будущее?
Ученики: Знание теории. (Слайд 7).
Учитель: Что называется уравнением?
Ученик: Равенство, содержащее переменную.
Учитель: Что такое корень уравнения?
Ученик: Значение переменной, при котором уравнение обращается в верное равенство.
Учитель: Что значит решить уравнение?
Ученик: Найти все его корни или доказать, что корней нет.
Путешествие в «прошлое».
-обобщение и систематизация знаний по решению уравнений за 7,8 класс.
Учитель: Самые первые уравнения, с которыми вы познакомились еще в начальной школе, продолжали их решать в 5,6, 7, какого вида это уравнения?
Ученик: Линейные. (Слайд 8).
Учитель: Основной алгоритм решения линейных уравнений?
Ученик: обобщает и систематизирует свои знания по теме «Решение линейных уравнений».
Учитель: Найти ошибку и решить правильно. (Слайд 9).
Ученики: находят и объясняют ошибки, называют правильный результат.
Учитель: Какие уравнения вы научились решать в 8 классе?
Ученик: Квадратные. (Слайд 10).
Учитель: Основные способы решения квадратных уравнений?
Ученик: обобщает и систематизирует свои знания по теме «Решение квадратных уравнений».
Учитель: Найти ошибку и решить правильно. (Слайд 11).
Ученики: находят и объясняют ошибки, называют правильный результат.
Учитель: Самые трудные и коварные уравнения?
Ученик: Дробные рациональные уравнения. (Слайд 12).
Учитель: Приемы решения?
Ученик: обобщает и систематизирует свои знания по теме «Решение дробных рациональных уравнений».
Учитель: Найти ошибку и решить правильно. (карточки).
Ученики: находят и объясняют ошибки, называют правильный результат.
Путешествие в «настоящее».
-закрепление, тренировка и отработка умений.
-обобщение и систематизация знаний по решению уравнений за 9 класс.
Учитель: А теперь двигаемся в настоящее. 9 класс. (Слайд 14). Решение уравнений более высоких степеней, чем вторая. Основные способы? Новый способ?
Далее в форме диалога происходит обобщение и систематизация знаний по теме «Решение целых уравнений». Так как при решении уравнения х5-9х3+20х=0 используется два приема: разложение на множители и замена, то это уравнение решается учеником на доске. Уравнения №1и №3 ребята решают в парах. Учитель проводит индивидуальные консультации по мере необходимости.
Путешествие в «будущее».
-актуализация субъективного опыта учащихся.
-применение знаний в «необычной» ситуации.
Учитель: А теперь давайте заглянем в будущее. Я вам предлагаю решить несколько уравнений, предлагаемых одиннадцатиклассникам на ЕГЭ. (Слайд 14).
Уравнение 9∙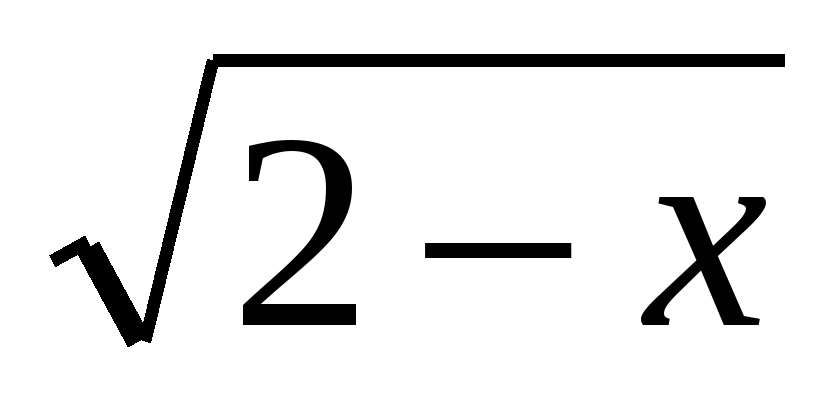 -х2∙
-х2∙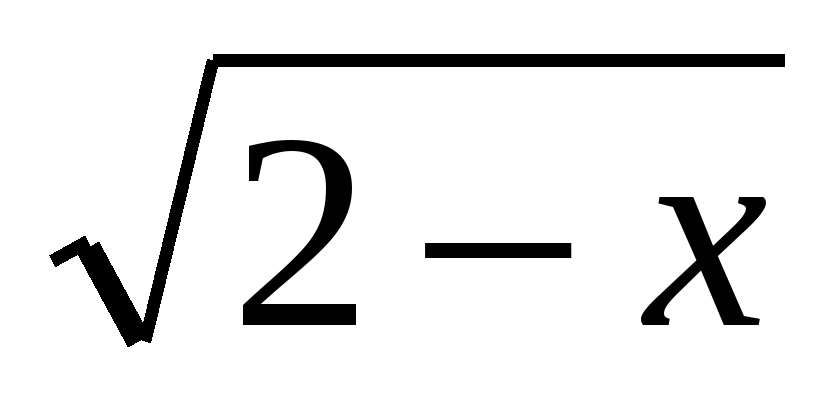 =0 решает учитель на доске. В результате решения получается три числа. Возникает проблемная ситуация: а все ли эти числа являются решениями данного уравнения? Что вы знаете про область определения арифметического квадратного корня?
=0 решает учитель на доске. В результате решения получается три числа. Возникает проблемная ситуация: а все ли эти числа являются решениями данного уравнения? Что вы знаете про область определения арифметического квадратного корня?
Уравнения х2-6х+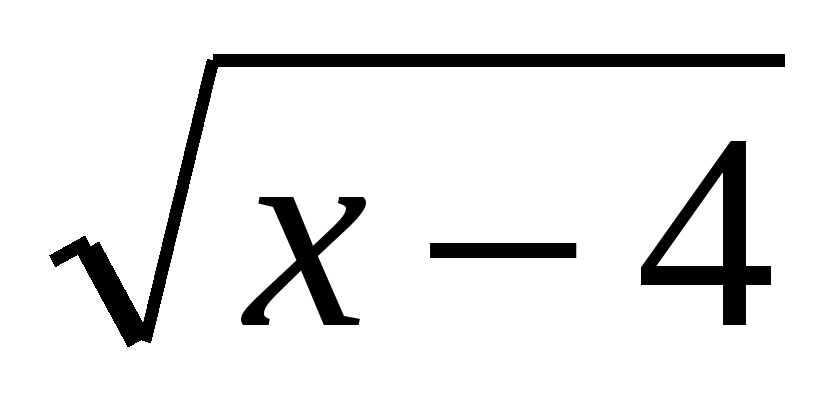 =
=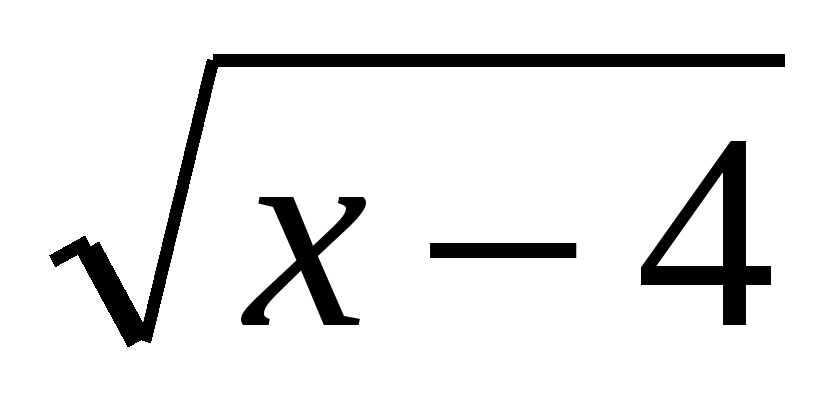 -5 и х2-5х-2=0∙
-5 и х2-5х-2=0∙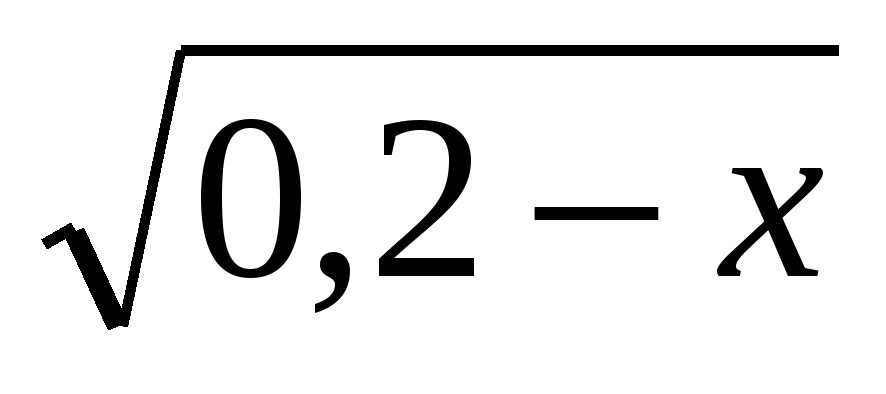 решают в парах.
решают в парах.
Информация о домашней работе.
(Слайд 15).
1. Учебник: № 295 (е,ж), 297 (а,б).
2. «Кто сказал, что в науке поэзии нет?
Нужно только понять и увидеть!»
М. Бромлей.
«Нельзя быть математиком, не будучи
одновременно поэтом в душе».
К. Вейерштрасс.
Творческое задание «Я и уравнения».
Самостоятельная работа.
(Слайд 16).
Учащиеся выполняют самостоятельную работу, выбирая для себя определенный уровень заданий (более простые - задания из «прошлого», более сложные - задания из «будущего»).
Критерии оценивания:
«3» - задания из «прошлого»;
«4» - задания из «настоящего»;
«5» - задания из «будущего».
Задания из «прошлого»
2-3(х+2)=5-2х
3х2+8х-3=0
Задания из «настоящего».
х4-2х2-8=0
х3+х2-х-1=0
Задания из «будущего».
1. (х2-7х+13)2-(х-3)(х-4)=1
х2∙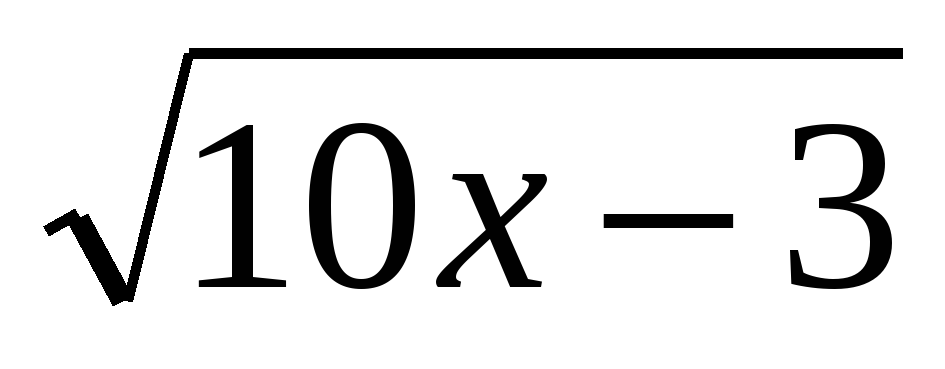 -х∙
-х∙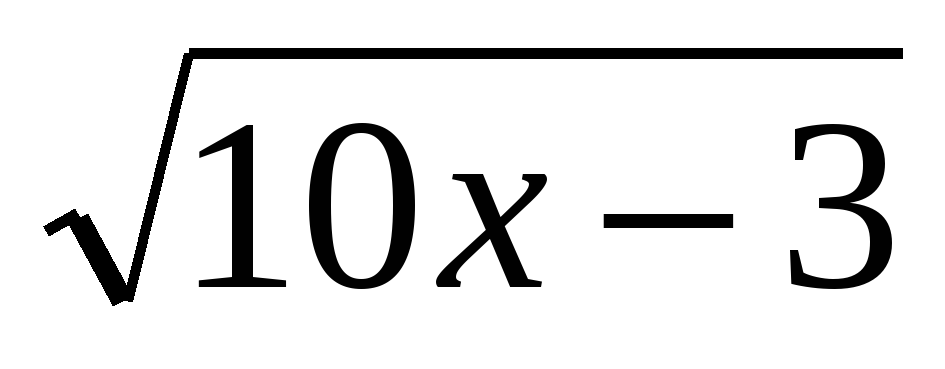 =0
=0
Учащиеся, решив уравнение, записывают ответ еще и на отдельный листок. Тетради с решениями сдают на проверку учителю. Сверяют свои ответы с правильными. (Слайд 17).
Этап рефлексии.
Оценив свои знания, эмоции учащиеся выбирают для себя открытку на память: свою машину времени: черепаху, лошадь, автомобиль, «машину времени». (Слайд 18).
Итог урока.
Что нового узнали на уроке?
Оцените свое настроение от путешествия.(Смайлы)
(Слайд 19)

















