Повышение деятельностного аспекта уроков математики через использование интерактивных и алгоритмических методов обучения.
Н.Л. Нечепурук, учитель математики
МБОУ «Трудовская средняя школа»
Сакского района Республики Крым
С переходом на новые образовательные стандарты перед учителем ставится новая задача – формирование деятельностной компетентности у учащихся. Сущностью деятельностной компетенции является познавательная деятельность, которая направлена на развитие активности и самостоятельности, с целью приобщения к поисковой и творческой деятельности.
Аспект деятельностной компетентности обучающихся направлен на реализацию следующих задач:
1. Развитие личностных компетентностей:
- формирование способности найти себя, развивать себя как личность;
- формирование коммуникативных качеств коллективно – групповой деятельности;
- формирование навыков убеждения.
2. Развитие мотивационных компетентностей:
- формирование способности к обучению;
- формирование самостоятельного мышления;
- формирование творческих способностей.
3. Развитие интерпретационных компетентностей:
- формирование навыков использовать полученную информацию;
- формирование навыков регулятивной деятельности;
- формирование стойких процессов усвоения знаний.
Результативность деятельностной компетентности зависит от регулятивных УУД, поэтому деятельность обучающихся – это сложный процесс. Он должен охватывать:
- знания, умения и навыки;
- творческие способности;
- жизненный опыт;
- умения ориентироваться в сложившейся ситуации;
- умения управлять своей деятельностью;
- умения понимать и правильно оценивать свою деятельность и деятельность других, проявлять толерантность в деятельности.
А что же такое деятельность?
Деятельность – это:
1) специфическая активность человека по познанию и преобразованию окружающей действительности.
2) работа, занятие в какой-либо области (большой современный толковый словарь русского языка. 2012).
Побуждает обучающихся к активной работе мотив, причина, желание или обязанность, которые влияют не только на деятельность, а на эффективность процесса, продуктивность и ее результат. А результат деятельности последовательной цепочкой взаимосвязан с такими этапами, как: создания условий, постановки проблем, мотивации, критического мышления учащихся, решение поставленных задач.
Главной целью является умелая организация деятельностной компетентности, направленной на формирование теоретических знаний, так как понятия составляют основную часть любой науки. Без понятий нельзя раскрыть существующие в объективной реальности связи, закономерности образования и развития математической оболочки, нельзя формировать научное мировоззрение, развивать учащихся, подводить их к ведущим идеям курса. Формирование обобщений и понятий считается основным ядром всего учебного процесса, это одна из главных целей обучения в школе. Не всегда учитель уделяет должного внимания обобщению существующих черт математических понятий, их свойственным характеристикам. Часто просто ограничивается определением понятий без особого раскрытия их сущности. Не устанавливаются связи и отношения формируемого понятия с другими понятиями. Нередко формирование понятий происходит без определенной опоры на свойства, представления. Поэтому, чаще всего, обобщающее повторение касается только фактического материала.
Чтобы наиболее эффективно организовать учебный процесс, необходимо четко знать, какие понятия следует формировать, в какой последовательности, какие существуют связи и взаимосвязи между ними.
Формирование понятий – это длительный и сложный путь, проходящий под руководством учителя и при большом умственном напряжении учителя.
Рассмотрим этапы формирования понятий через организацию деятельностного аспекта.
Первый этап включает введение нового понятия, то есть раскрытие его существенных признаков. Деятельностный аспект характеризуется осмыслением существенных признаков понятия и применением его в заданной ситуации. Можно использовать алгоритм, в котором учащимся предлагают во втором столбике написать или нарисовать признак. Чаще дети рисуют. Например, уже дан первый признак равенства треугольников. Предлагаем посмотреть на второй рисунок. В данном случае нет записи в первом столбике. Переходим к целеполаганию и изучению нового материала.
Равенство треугольников
Три угла
Три стороны
1 признак



![]()
?
![]()



![]()
3 признак
![]()
![]()


![]()
![]()
Эти рисунки помогают и при создании игровой ситуации «Молчанка», когда обучающиеся показывают руками определения равенства треугольников.
Второй этап - расширение объема материала (знакомство с новыми объектами относящимися к этому понятию) и углубление содержания понятия. На этом этапе используется теория для приобретения навыков, способствующих формированию теоретического мышления через закрепление существенных признаков понятий, а также применение их в качестве метода познания нового материала.
Например, учащимся предлагается составить алгоритм сложения и вычитания целых чисел. Чаще всего даю это при работе в парах при изучении и закреплении нового материала или задание домой, как творческое:
Сложение целых чисел
![]()
Посмотри на знак

нет
Одинаковые знаки
Разные знаки
![]()
![]()
![]()
да да
1. Сложить модули чисел.
2. Перед суммой поставить знак целых чисел
1. Найти больший модуль.
2. Из большего модуля вычесть меньший модуль.
3. Поставить знак большего модуля.
Третий этап формирования понятий – это отнесение его к определенной системе, раскрытие связей между отдельными системами. Мы часто встречаемся с фактом, когда после изучения вертикальных углов по геометрии, переходим на изучение параллельность прямых после изучения признаков равенства треугольников, то учащиеся забывают понятия из ранее изученного или не могут связать ранее изученный материал с новым. Поэтому при изучении параллельности прямых необходимо обратить внимание на образование углов. Начать со смежных углов, вертикальных, а потом перейти на новые понятия. То есть создать систему взаимосвязи понятий в геометрии. Значительную помощь при формировании понятий может оказать организация деятельностного подхода при работе с учебником, в котором отражены основные этапы и пути развития знаний, понятий, умений, учтены условия успешного самопознания и развития самостоятельности.
Я убеждена, что деятельностный аспект уроков математики достигается через внедрение в учебный процесс интерактивного и проблемного обучения. Не буду описывать технологию интерактивного обучения. Приведу несколько примеров использования элементов такого обучения на уроках математики, алгебры, геометрии.
1. Метод «Пометок» (засечки, корректор). Например, при изучении темы «Целые числа», учащимся предлагаю поставить на полях пометки: + - я это знаю, ˅ - слышал, но забыл или не знал, где применяется, - - не знал, ? – я удивлен.
2. Метод «Ассоциативный куст» (часто называю «солнышко» или «мозговой штурм»). При изучении темы «Тождественные треугольники».
![]() 3угла
3угла

 3 стороны тупоугольные
3 стороны тупоугольные

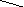 остроугольные равнобедренные
остроугольные равнобедренные
Треугольни- ки
![]()
![]() равносторонние разносторонние
равносторонние разносторонние


![]()

 сумма углов=180˚ прямоугольный
сумма углов=180˚ прямоугольный
3 признака равенства 3признака тождественности
Тождественные
Можно и предложить обучающимся и рассмотреть данный «ассоциативный куст». Поставить проблему: «Расскажите о каждом понятии». Учащиеся некоторые начинают предполагать, что равные и тождественные – это одно и тоже. Отсюда выходим на целеполагание. Дается задание: используя метод «ПРЕСС» (описан ниже) и самообучение по учебнику составить сообщение на тему «Тождественные треугольники».
3. Метод «Микрофон». Можно использовать «ассоциативный куст» как «микрофон», когда учащимся предлагают дополнить что-то быстро, по очереди. Говорить должны все, можно повторять чьи-то слова, но добавляя своё.
4. Метод «ПОПС» или метод «ПРЕСС». Даёт возможность развивать коммуникативные УУД, развивать математическую правильную речь. Этапы метода:
1. Позиция (понятие, определение понятия…).
2. Обоснование (Я думаю…высказывание своей мысли).
4. Пример (пример, факты, то, что подтверждает позицию).
5. Следствие (вывод, поэтому…).
5. Метод «Займи позицию». Учащимся предлагаю посмотреть на рисунок и занять позицию: 1группа – те, кто считает, что задача решается через 1 признак параллельности двух прямых, 2группа – те, кто считает, что задача решается через 2 признак параллельности прямых, 3группа – те, кто считает, что задача решается через 3 признак параллельности прямых.
Учащиеся работают в группах. Затем доказывают свою точку зрения. Все вместе делают вывод, что можно решить разным способом, но выбирают наиболее рациональный.
6. Метод «Домино». Хорошо использовать на повторение или проверку теоретических знаний. При организации работы в парах учащимся предлагается сыграть в математическое домино. Первый учащийся выкладывает начало предложения, а второй находит продолжение. Потом меняются. Предлагаю несколько вопросов в таблице, которую нужно разрезать:
| Объясните, какая фигура называется треугольником? | Фигура, состоящая из трех точек, не лежащие на одной прямой, и соединенных отрезками, называется треугольник |
| Что такое периметр треугольника?
| Сумма длин трех сторон треугольника называется его периметром.
|
| Какие треугольники называются равными? | Два треугольника, называются равными, если их можно совместить наложением |
| Какой отрезок называется медианой треугольника? | Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треуголь ника |
| Какой отрезок называется биссектрисой треугольника? | Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называ ется биссектрисой треугольника |
| Какой отрезок называется высотой треугольника? | Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника |
| Первый признак равенства треугольников. | По двум сторонам и углу между ними |
| Второй признак равенства треугольников. | По стороне и двум прилежащим углам |
| Третий признак равенства треугольников. | По трем сторонам |
Деятельностный аспект уроков математики достигается и через создание проектов - алгоритмов развития навыков и умений. Учащиеся с удовольствием создают свои алгоритмы, схемы, что позволяет запомнить порядок выполнения поставленной задачи так, чтобы именно им было понятно. Эти проекты - алгоритмы они защищают и хранят в портфолио своих учебных достижений. Создание алгоритмов активизирует познавательный интерес учащихся, развивает их творческую активность.
По мнению Л.Н. Нестеровой развитие творческой активности повышает:
1. Стремление к самостоятельному выполнению намеченных задач.
2. Стремление раскрыть суть изучаемых вопросов.
3. Стремление раскрыть причинные зависимости, выявить доказательность научных положений в ходе решения поставленных задач.
По мнению Г.И. Щукиной на развитие творческой активности влияют следующие компоненты познавательных интересов:
1. Эмоциональная деятельность (переживание по отношению к объектам, увлеченность процессом деятельности, положительное отношение к ней).
2. Интеллектуальная деятельность (стремление к исследованию, к решению поставленных задач, проникновение вглубь проблемы).
3. Волевая деятельность (стремление к самостоятельности как в повторении и обобщении полученных знаний, так и в добывании новых).
Я убеждена, что развитие творческой активности может быть средством воспитания качественного творческого мышления через умения учащихся создавать алгоритмы обучения. Алгоритмы я называю решение задач через постановку проблемной ситуации: как решить, каким способом, создать план решения. Приведу несколько примеров минипроектов – алгоритмов, созданных учащимися.
1.Алгоритм сравнения десятичных дробей
Сравнение десятичных дробей
![]()
Посмотри на количество знаков после запятой

Разное количество
Одинаковое количество
![]() нет
нет
![]()
![]()
да да
1. Уравнять количество знаков после запятой (например, 64,5 и 64,521).
Сравнить, не обращая внимания на запятую
![]()
1. Допишем в первой дроби необходимое количество нулей, чтобы уравнять количество знаков после запятой(например, 64,500 и 64,521).
2. Сравним натуральные числа: 64500 и 64521.
2. Алгоритм решения уравнения вида ах2+вх=0 (с=0)
Уравнение
ах2+вх=0 (с=0)
![]()
Вынеси за скобки общий множитель: х(ах+в)=0.
![]()
Произведение равно 0, если хотя бы один из множителей равен 0, значит: х=0 или ах+в=0.
![]()
Реши каждое из полученных уравнений
![]()
![]()
ах+в=0
ах= - в
х = - в/а
х2 = - в/а
х=0
![]()
Х1=0


Запиши ответ.
Ответ: х1= 0, х2= -в/а
Литература:
1. Нестерова Л.Н. Стимулирование творческой активности учащихся в процессе обучения. Автореф. дисс. к.п.н. - М., 1967. — 16 с.
2. Суворова Н. Интерактивное обучение: Новые подходы. - М., 2005. – 167 с.
3. Щукина Г.И. Развитие познавательной активности школьников. М., 1989, —142 с.
4. Байдак В.А. и др. Формирование алгоритмической культуры у учащихся. – М.: Просвещение, 1989.
5. Полюхова Т.В. Методическое пособие. Алгоритмы в школьном курсе математики. – 2013г.















 3 стороны тупоугольные
3 стороны тупоугольные
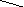 остроугольные равнобедренные
остроугольные равнобедренные 









