Практическая работа №45 «Построение графиков»

Практическая работа №45 «Построение графиков»

Цель работы: Обобщить и систематизировать знания по теме «Графики функции». Закрепить умения использовать полученные знания для построения и чтения графиков функций.

Теоретические сведения к практической работе:

Общая схема исследования функции:

1. Найти область определения функции. Выделить особые точки (точки разрыва).

2. Установить, является ли функция чётной или нечётной.

Функция называется четной если 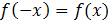  и ее график симметричен относительно оси  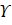 ; если  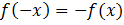 для всех x из данного множества, то функция называется нечетной, и ее график симметричен относительно начала координат.

1. Найти точки пересечения с осями координат (если это не вызывает затруднений).

2. Определить, является ли функция периодической или нет (только для тригонометрических функций, остальные непериодические, пункт пропускается).

3. Найти точки экстремума и интервалы монотонности (возрастания и убывания) функции.

Вычислить производную функции. Найти критические точки – точки, в которых производная равна нулю или не существует. Определить знак производной на каждом из интервалов слева и справа от критических точек. Где производная положительная, функция монотонно возрастает, а на интервалах, где производная отрицательная – функция убывает.

1. Найти точки перегиба и интервалы выпуклости-вогнутости.

Вычислить вторую производную функции. Найти точки, в которых вторая производная равна нулю или не существует. Определить знак производной на каждом из интервалов. Где вторая производная положительная, функция вогнута, а на интервалах, где вторая производная отрицательная – функция выпукла. Точки, в которых вторая производная меняет свой знак, являются точками перегиба функции.

1. Используя полученные сведения, построить график функции.

Задания для самостоятельного решения

Вариант 1

Исследовать функцию с помощью производной и построить ее график

1. y=x³- 6x²+9x-3

2. y= -x⁴+2x²+3

3. y =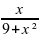 

Вариант 2

Исследовать функцию с помощью производной и построить ее график

1. y =- 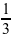  x³ +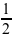  x² + 1

2. y=x³+ 6x²+9x+8

3. y =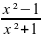 

Контрольные вопросы:

1. Что такое график?

2. В какой последовательности исследуется график?