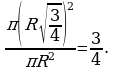Практическая работа №65 «Решение задач по теме шар и сфера»
Цель работы: Обобщить и систематизировать знания по теме «Элементы сферы и шара». Совершенствовать умения и навыки решения геометрических задач.
Теоретические сведения к практической работе:
Шаром принято называть тело, ограниченное сферой, т.е. шар и сфера – это разные геометрические тела.
Сфера– это фигура, состоящая из всех точек пространства, удалённых от данной точки на данном расстоянии.
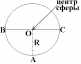

Поверхность шара называют сферой.Если рассечь сферу плоскостью, получим в сечении окружность. Такие окружности имеют разные радиусы: чем дальше плоскость от центра сферы, тем меньше радиус сечения. Самые большие окружности получаются при сечении сферы плоскостями, проходящими через её центр. Такими большими окружностями на земной поверхности являются экватор и меридианы. А параллели–это сечения земной поверхности плоскостями, которые параллельны экваториальной плоскости.
Сферойназывается фигура, состоящая из всех точек пространства, равноудалённых от данной точки. Эта точка называетсяцентром сферы и обычно обозначается О.
Расстояние от точек сферы до её центра называетсярадиусом сферы и обычно обозначается R.Радиусомтакже называется любой отрезок, соединяющий точку сферы с её центром.Сфера–это граница шара. Центр, радиус и диаметр сферы являются также центром, радиусом и диаметром шара.
Шаромназывается тело, которое состоит из всех точек пространства, находящихся на расстоянии не более чем на данное расстояние. Другими словами,шар– это объединение сферы и всех ее внутренних точек.
Всякоесечение шараплоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость.
Площадь сферы: S=4πr2=πd2.
Взаимное расположение сферы и плоскости:



Касательная плоскость к сфере
П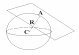 лоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка называется точкой касания плоскости и сферы.
лоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка называется точкой касания плоскости и сферы.
Радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.
Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной к сфере.
Сечение шара
В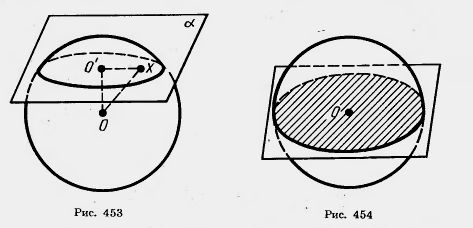 сякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость.
сякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость.
Пример 1.
Два сечения шара радиуса 10 см параллельными плоскостями имеют радиусы, равные 6 см и 8 см. Найти расстояние между секущими плоскостями.
Решение:
находим расстояние каждой из параллельных плоскостей до центра шара из прямоугольных треугольников по теореме Пифагора:
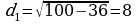 см
см
или
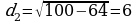 см.
см.
В зависимости от того, лежит ли центр шара между плоскостями или нет, получаем два различных ответа к задаче:
d=14 см.
Пример 2.
Ч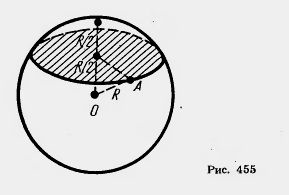 ерез середину радиуса шара проведена перпендикулярная ему плоскость. Как относится площадь полученного сечения к площади большого круга ?
ерез середину радиуса шара проведена перпендикулярная ему плоскость. Как относится площадь полученного сечения к площади большого круга ?
Решение:
отношение площади круга к площади полученного сечения равно:
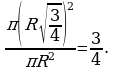
Задания для самостоятельного решения:
1) Шар, радиус которого равен 41 дм, пересечен плоскостью на расстоянии 9 дм от центра. Вычислите площадь получившегося сечения.
2) Через середину радиуса шара проведена перпендикулярная к нему плоскость. Как относится площадь полученного сечения к площади большого круга?
3) Радиус шара равен 63см. Точка находится на касательной плоскости на расстоянии 16 см от точки касания. Найти ее кратчайшее расстояние от поверхности шара.
4) Радиус шара R. Через конец радиуса проведена плоскость под углом в 600 к нему. Найти площадь сечения.
5) На поверхности шара даны три точки. Прямолинейные расстояния между ними: 6 см, 8 см и 10 см. Радиус шара равен 13см. Радиус шара равен 13см. Найти расстояние от центра шара до плоскости, проходящей через эти три точки.
Контрольные вопросы:
-
Дайте определение шара, сферы.
-
Запишите формулы площади сферы, объема шара.
-
Приведите примеры взаимного расположения сферы и плоскости.












 лоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка называется точкой касания плоскости и сферы.
лоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка называется точкой касания плоскости и сферы. сякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость.
сякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость. 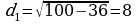 см
см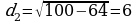 см.
см. ерез середину радиуса шара проведена перпендикулярная ему плоскость. Как относится площадь полученного сечения к площади большого круга ?
ерез середину радиуса шара проведена перпендикулярная ему плоскость. Как относится площадь полученного сечения к площади большого круга ?