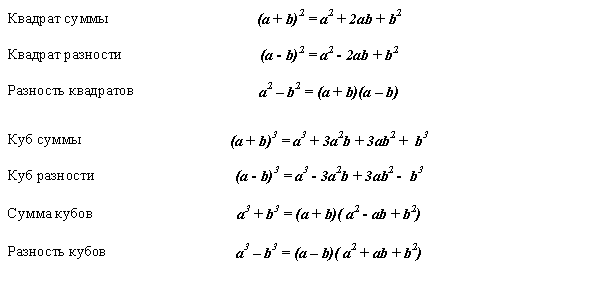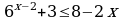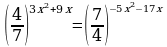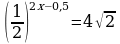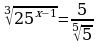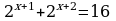Просмотр содержимого документа
«Практическая работа №8 «Преобразование степенных выражений»»
Практическая работа №8 «Преобразование степенных выражений»
Цель работы: Обобщить и систематизировать знания по теме «Системы иррациональных уравнений»; закрепить умения использовать полученные знания для решения иррациональных уравнений
Теоретические сведения к практической работе:
Корни натуральной степени из числа, их свойства.
Корень n – степени: 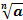 , n - показатель корня, а – подкоренное выражение
, n - показатель корня, а – подкоренное выражение
Если n – нечетное число, то выражение 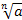 имеет смысл при
имеет смысл при 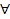 а
а
Если n – четное число, то выражение 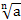 имеет смысл при
имеет смысл при 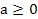
Арифметический корень: 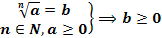
Корень нечетной степени из отрицательного числа: 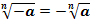
Основные свойства корней:
1. Правило извлечения корня из произведения: 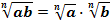
2. Правило извлечения корня из дроби: 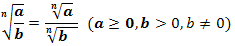
3. Правило извлечения корня из корня: 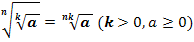
4. Правило вынесения множителя из под знака корня: 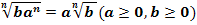
5. Внесение множителя под знак корня: 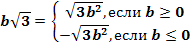
6. Показатель корня и показатель подкоренного выражения можно умножить на одно и тоже число. 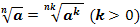
7. Правило возведения корня в степень. 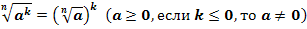
Степень с натуральным показателем
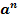 =
=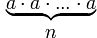 ,a – основание степени, n – показатель степени
,a – основание степени, n – показатель степени
Свойства:
1. При умножении степеней с одинаковыми основаниями показатели складываются, а основание остается неизменным. 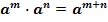
2. При делении степеней с одинаковыми основаниями показатели вычитаются, а основание остается неизменным. 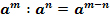
3. При возведении степени в степень показатели перемножаются. 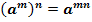
4. При возведении в степень произведения двух чисел, каждое число возводят в эту степень, а результаты перемножают. 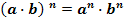
5. Если в степень возводят частное двух чисел, то в эту степень возводят числитель и знаменатель, а результат делят друг на друга. 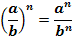
6. Если 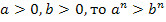
Степень с целым показателем
1. 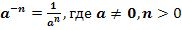
2. 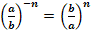
3. 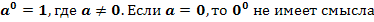
4. По определению: 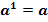
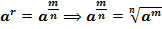
Свойства:
1. 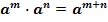
2. 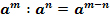
3. 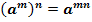
4. 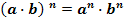
5. 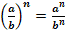
6. Пусть r рациональное число 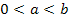 , тогда
, тогда
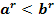 при r0
при r0 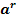
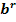 при r
при r
7 .Для любого рациональных чисел r и s из неравенства 
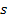 следует
следует
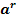
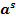 при a1
при a1 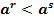 при
при 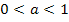
Формулы сокращённого умножения.
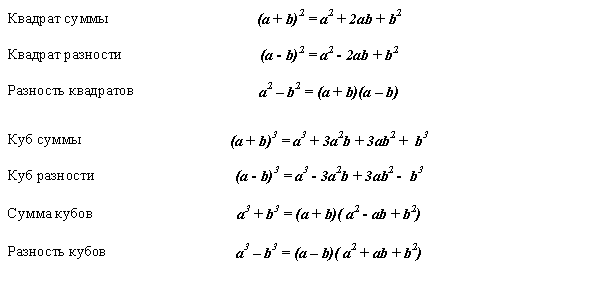
Задания для самостоятельного решения:
1 вариант
Найдите значение выражения
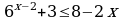
Упростите
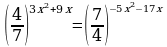
Вычислите
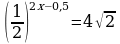
Упростите выражение
а)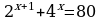
б) 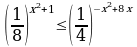
2 вариант
Найдите значение выражения
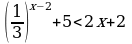
Упростите
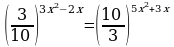
Вычислите
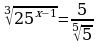
Упростите выражение
а)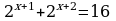
б) 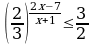
Контрольные вопросы:
Что называется корнем n – степени?
Что такое арифметический корень?
Что называется корнем нечетной степени из отрицательного числа?