«Парабола и модуль»
Автор: Спирякова А.А.
Квалификационная категория: высшая
Стаж работы: 19 лет
Место работы: МКОУ Тогучинского района «Тогучинская средняя школа № 4»
Должность: учитель математики
2019 год.
Оглавление:
Введение___________________________________________________ 2
Основная часть.
Из истории____________________________________________ 3
Информация о параболе и модуле: определения, свойства, правила _______________________________________________ 5
Построение графика квадратичной функции, содержащей переменную под знаком модуля__________________________ 5
Практические задачи из ОГЭ_____________________________10
Заключение________________________________________________ 11
Литература___________________________________________ 12
Приложение_______________________________________________ 13
Введение.
Почему из всех функций, изучаемых в школе (линейная, гипербола, квадратичная парабола, кубическая парабола, квадратного корня), я выбрала именно квадратичную параболу? Потому что считаю её более изящной и красивой. Всё, что нас окружает, так или иначе связано с параболой. Параболу можно встретить в объектах, созданных человеком, в природе, в различных областях науки. (Приложение 1.) Квадратичная функция обладает интересными свойствами, с которыми учащиеся познакомятся на уроках алгебры в 7 классе, а в 9 классе научатся строить график функции 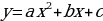 по алгоритму. Решая задачи ОГЭ под номером 23, я часто встречаю графики функций, содержащих модуль. Поэтому решила предложить учащимся выяснить, как будет выглядеть график параболы в зависимости от расположения знака модуля.
по алгоритму. Решая задачи ОГЭ под номером 23, я часто встречаю графики функций, содержащих модуль. Поэтому решила предложить учащимся выяснить, как будет выглядеть график параболы в зависимости от расположения знака модуля.
Цель работы:
Выяснить, какой вид принимает график квадратичной функции, содержащей переменную под знаком модуля.
Задачи:
Изучая литературу и интернет – ресурсы, найти информацию о квадратичной функции и модуле.
Провести исследования в области построения параболы, содержащей модуль.
Выяснить, существует ли какая – то закономерность в построении таких графиков.
Объект исследования:
- парабола и модуль.
Предмет исследования:
- изменение графика квадратичной функции, содержащей модуль.
Методы исследования:
Наблюдение, построение, обобщение, систематизация, моделирование, изучение справочной литературы и поиск информации в глобальных компьютерных сетях.
Гипотеза:
Каждый график квадратичной функции, содержащей переменную под знаком модуля, имеет свою особенность или у них есть что – то общее.
Основная часть.
Из истории.
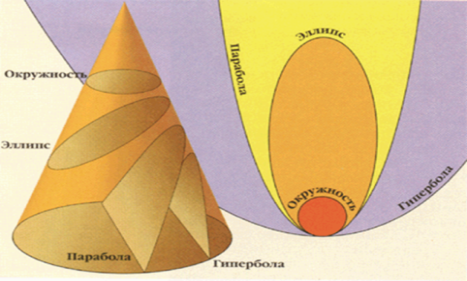
Рис 1.
С древних времен кривые привлекали к себе внимание ученых и использовались ими для описания различных природных явлений. Одним из первых, кто начал изучать эти кривые, был ученик знаменитого Платона, древнегреческий математик Менехм (IVв. До н.э.). Изменяя угол при вершине конуса, Менехм получил три вида кривых: эллипс – если угол при вершине конуса острый; параболу – если угол прямой; одну ветвь гиперболы – если угол тупой. Древнегреческий математик Аполлоний Пергский, (прославившийся монографией
“Конические сечения”, в которой изложил общую теорию параболы, гиперболы и эллипса) предложил общепринятые названия этих кривых, до него их называли просто «сечениями конуса». (Приложение 2).
Определение параболы:
Парабола – это литературный жанр, который представляет собой небольшой самостоятельный рассказ иносказательного характера, имеющий поучительный смысл и особую форму повествования, которое движется как бы по кривой (параболе): начатый с отвлеченных предметов, рассказ постепенно приближается к главной теме, а затем вновь возвращается к началу, например, «Старик и море». (Словарь литературоведческих терминов, 2012)
Парабола – от греч. (parabole) плоская кривая (2-го порядка). Парабола - множество точек М, расстояния которых до данной точки F (фокуса) и до данной прямой D1D2 (директрисы) равны. В надлежащей системе координат уравнение параболы имеет вид: 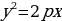 , где р=2OF. (Большой энциклопедический словарь, 2012)
, где р=2OF. (Большой энциклопедический словарь, 2012)
Считается, что термин «модуля» впервые ввел в пользование английский математик и философ Роджер Котс, который в свою очередь являлся учеником знаменитого ученого Исаака Ньютона. Великий немецкий физик, изобретатель, математик и философ Готфрид Лейбниц также в своих работах и трудах использовал функцию модуля, которую он обозначил mol x. Однако, уже общепринятое и современное значение модуля как абсолютной величины было дано еще в 1841 году выдающимся немецким математиком Карлом Вейерштрассом. В начале девятнадцатого века ученые Арган и Коши ввели данное понятие и для комплексных чисел. На сегодняшний день, так как функция модуля вычисляется очень просто, ее ввели и список стандартных функций фактически всех языков программирования.
Слово «модуль» произошло от латинского слова «modulus», что в переводе означает «мера». Это многозначное слово (омоним), которое имеет множество значений и применяется не только в математике, но и в архитектуре, физике, технике, программировании и других точных науках.
В архитектуре - это исходная единица измерения, устанавливаемая для данного архитектурного сооружения и служащая для выражения кратных соотношений его составных элементов.
В технике - это термин, применяемый в различных областях техники, не имеющий универсального значения и служащий для обозначения различных коэффициентов и величин, например модуль зацепления, модуль упругости.
Модуль объемного сжатия (в физике)-отношение нормального напряжения в материале к относительному удлинению.
Информация о параболе и модуле: определения, свойства, правила.
Определение. Модуль числа a или абсолютная величина числа a равна a, если a больше или равно нулю и равна -a, если a меньше нуля:

Из определения следует, что для любого действительного числа а, 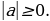
Функция 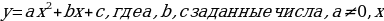 – независимая переменная, называется квадратичной функцией. Графиком квадратичной функции является кривая, называемая параболой. В уравнении квадратичной функции: а – старший коэффициент, b – второй коэффициент, с – свободный член.
– независимая переменная, называется квадратичной функцией. Графиком квадратичной функции является кривая, называемая параболой. В уравнении квадратичной функции: а – старший коэффициент, b – второй коэффициент, с – свободный член.
Алгоритм построения квадратичной функции:
Найти координаты вершины параболы и отметить её на координатной плоскости: абсциссу m вершины можно найти по формуле 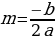 , ординату n можно найти, подставив найденное значение абсциссы в формулу
, ординату n можно найти, подставив найденное значение абсциссы в формулу 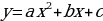 .
.
Через вершину параболы провести ось симметрии параллельно оси ОУ.
Найти нули функции: чтобы найти нули функции достаточно решить уравнение 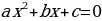 , корни уравнения - абсциссы точек пересечения с осью ОХ.
, корни уравнения - абсциссы точек пересечения с осью ОХ.
Построить ещё несколько точек, принадлежащих параболе.
Соединить отмеченные точки плавной линией.
Построение графика квадратичной функции, содержащей переменную под знаком модуля
Построим график функции 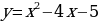 по алгоритму.
по алгоритму.
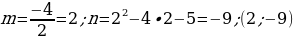
Ч ерез вершину параболы проведём ось симметрии параллельно оси ОУ.
ерез вершину параболы проведём ось симметрии параллельно оси ОУ.
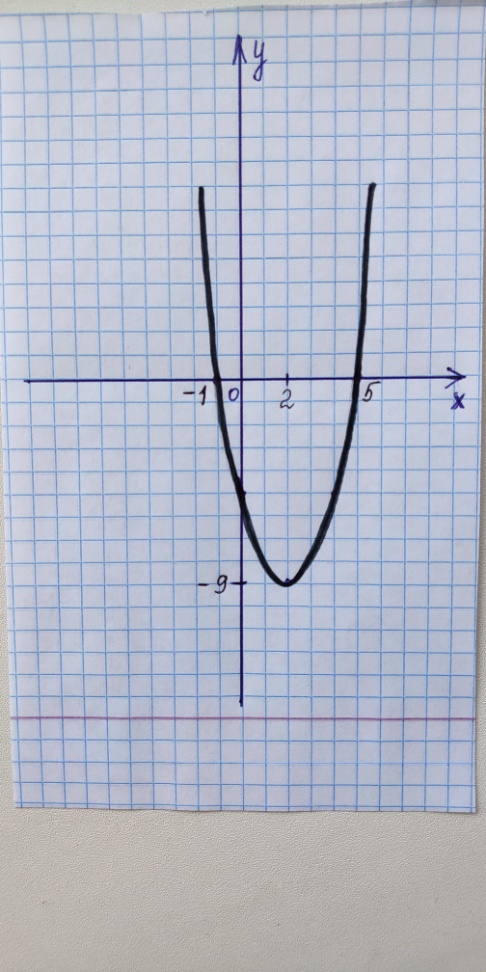
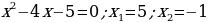
Рис. 2
Исследование 1. Построим график функции 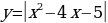 .
.
 Воспользуемся определением модуля и рассмотрим два случая:
Воспользуемся определением модуля и рассмотрим два случая:
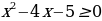 , тогда
, тогда 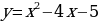 и выделим все точки с положительной ординатой:
и выделим все точки с положительной ординатой: 
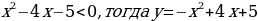 и выделим все точки с положительной ординатой
и выделим все точки с положительной ординатой 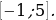
Рис. 3
Вывод: для построения графика функции 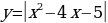 надо сохранить ту часть графика функции
надо сохранить ту часть графика функции 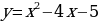 , точки которой находятся на оси ОХ или выше оси ОХ и симметрично отразить относительно оси ОХ ту часть графика функции
, точки которой находятся на оси ОХ или выше оси ОХ и симметрично отразить относительно оси ОХ ту часть графика функции 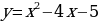 , которая расположена ниже оси ОХ.
, которая расположена ниже оси ОХ.
Исследование 2. Построим график функции 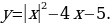
Так как 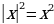 , то график функции
, то график функции 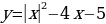 совпадает с графиком функции
совпадает с графиком функции 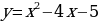 .
.
 Вывод: график функции
Вывод: график функции 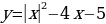 совпадает с графиком функции
совпадает с графиком функции 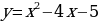 .
.
Рис. 4
Исследование 3. Построим график функции 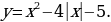
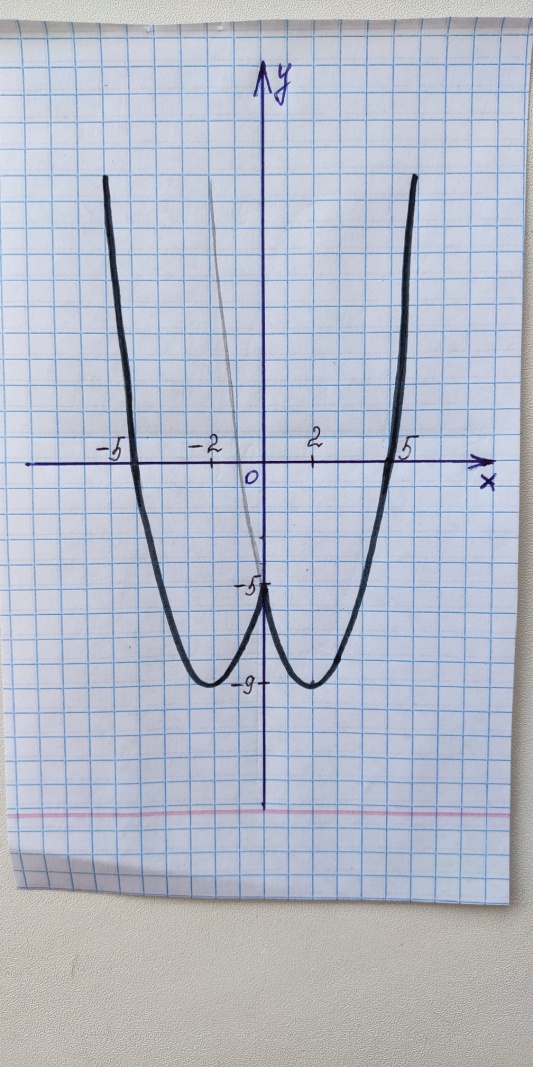 Воспользуемся определением модуля и рассмотрим два случая:
Воспользуемся определением модуля и рассмотрим два случая:
Пусть 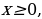 тогда
тогда 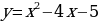 . Построим параболу
. Построим параболу 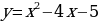 и обведём ту её часть, которая соответствует положительным значениям х.
и обведём ту её часть, которая соответствует положительным значениям х.
Пусть 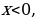 тогда
тогда 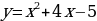 . Построим параболу
. Построим параболу 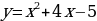 и обведём ту её часть, которая соответствует отрицательным значениям х.
и обведём ту её часть, которая соответствует отрицательным значениям х.
Рис. 5
Вывод: Для построения графика функции 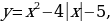 надо сохранить ту часть графика функции
надо сохранить ту часть графика функции 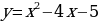 , где
, где  и симметрично отразить эту часть графика относительно оси ОУ.
и симметрично отразить эту часть графика относительно оси ОУ.
Исследование 4. Построим график функции 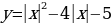 .
.
Так как 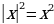 , то график функции
, то график функции 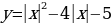 совпадает с графиком функции
совпадает с графиком функции 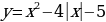 .
.

Вывод: график функции 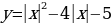 совпадает с графиком функции
совпадает с графиком функции 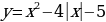 .
.
Рис. 6
Исследование 5. Построим график функции 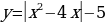 .
.
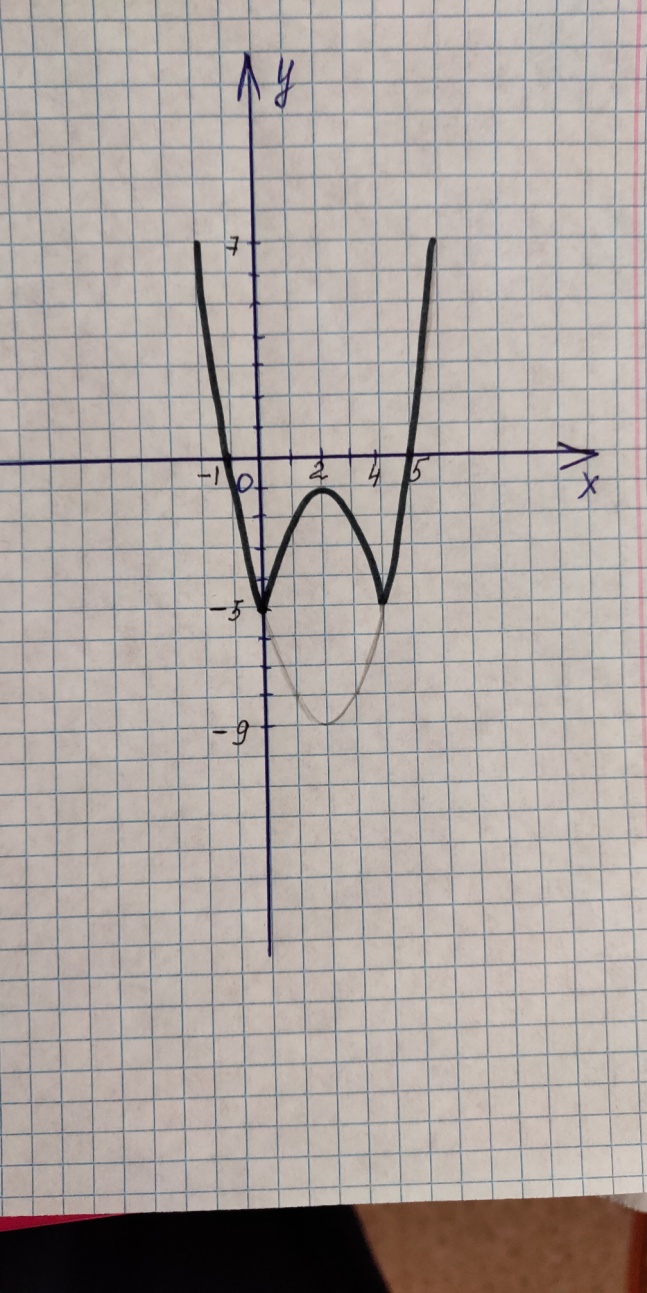 Воспользуемся определением модуля и рассмотрим два случая:
Воспользуемся определением модуля и рассмотрим два случая:
Решим неравенство 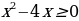 , построим график функции
, построим график функции
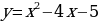 на интервале
на интервале  .
.
Решим неравенство 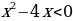 , построим график функции
, построим график функции
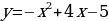 на интервале
на интервале 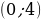 .
.
Г
Рис. 7
рафик функции
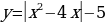
можно построить другим способом: построить график функции
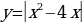
и опустить его на пять единиц вдоль оси ОУ.
Вывод: График функции 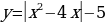 можно построить из графика функции
можно построить из графика функции 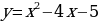 , если изобразить зеркально ту часть графика, которая лежит ниже прямой у = - 5.
, если изобразить зеркально ту часть графика, которая лежит ниже прямой у = - 5.
Исследование 6. Построим график функции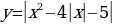 .
.
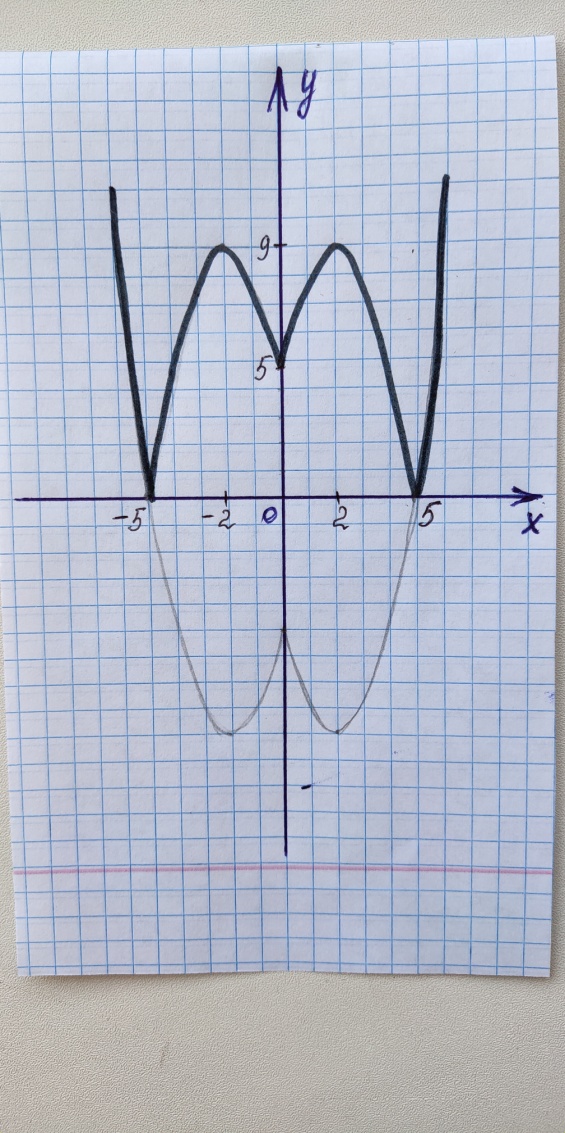 Воспользуемся результатами проделанной работы и обратимся к исследованию № 1 и № 3. Тогда график функции
Воспользуемся результатами проделанной работы и обратимся к исследованию № 1 и № 3. Тогда график функции 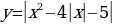 можно построить так: построить график функции
можно построить так: построить график функции 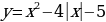 и ту часть графика, которая находится под осью ОХ изобразить зеркально относительно этой оси.
и ту часть графика, которая находится под осью ОХ изобразить зеркально относительно этой оси.
В
Рис. 8
ывод: построить график функции
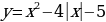
и ту часть графика, которая находится под осью ОХ изобразить зеркально относительно этой оси.
Исследование 7. Построим график функции 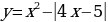 .
.
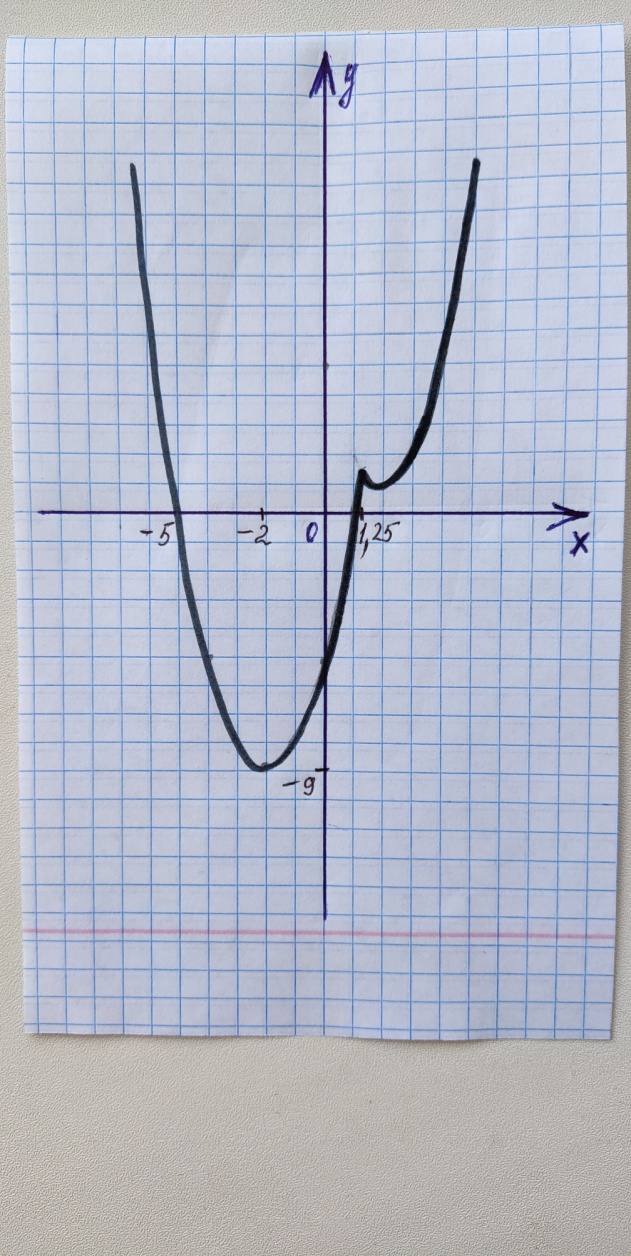 Выясним, при каком значении х выражение, стоящее под знаком модуля, равно нулю:
Выясним, при каком значении х выражение, стоящее под знаком модуля, равно нулю: 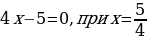 .
.
Рассмотрим два случая:
а) 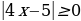 , при
, при 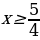 , тогда функция
, тогда функция 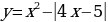 примет вид
примет вид 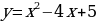 . Построим эту функцию на интервале
. Построим эту функцию на интервале  .
.
 б
б
Рис. 9
)
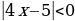
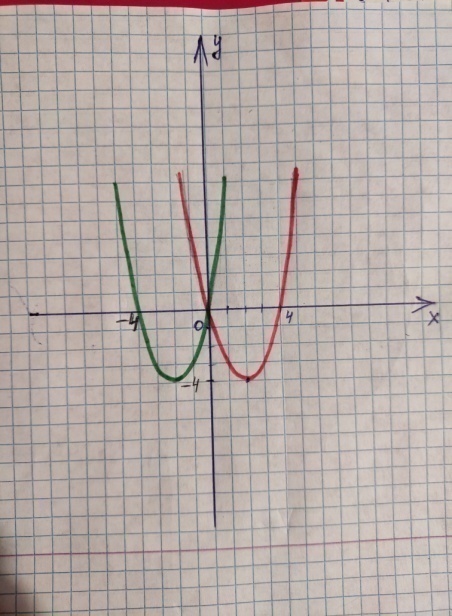
, при
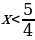
, тогда функция
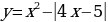
примет вид
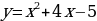
. Построим данную функцию на интервале
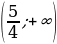
.
В
Рис. 10
ывод: график функции
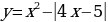
можно получить, если построить график функции
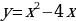
и поднять его на пять единиц вдоль оси ОУ (справа на рисунке), и если построить график функции
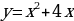
и опустить его на пять единиц вдоль оси ОУ (слева на рисунке).
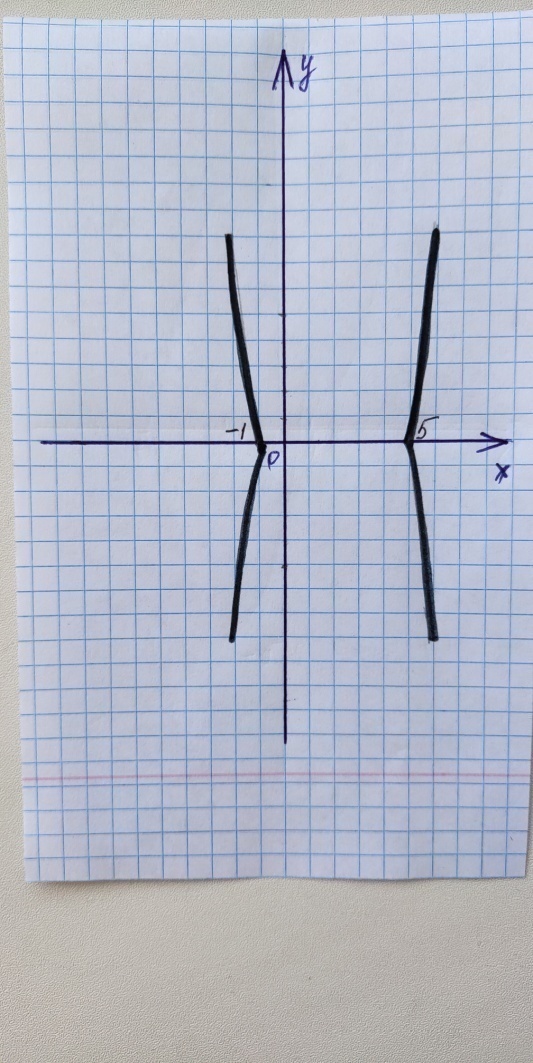
Исследование 8. Построим график 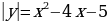 .
.
 М
М
Рис. 11
одуль – величина положительная, следовательно, правая часть данного равенства тоже величина положительная. Решая,
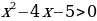
, получаем, что заданному значению х соответствует два значения у. Потому данная зависимость не является функцией. Раскроем модуль и построим график уравнения с двумя переменными. При
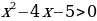
, получим
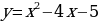
, при
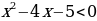
, получим
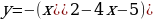
.
Вывод: Зависимость 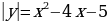 не является функцией. Чтобы её изобразить достаточно, начертить ту часть графика, которая лежит ниже оси ОХ, оставшуюся часть симметрично изобразить относительно оси ОХ.
не является функцией. Чтобы её изобразить достаточно, начертить ту часть графика, которая лежит ниже оси ОХ, оставшуюся часть симметрично изобразить относительно оси ОХ.
Практические задачи из ОГЭ
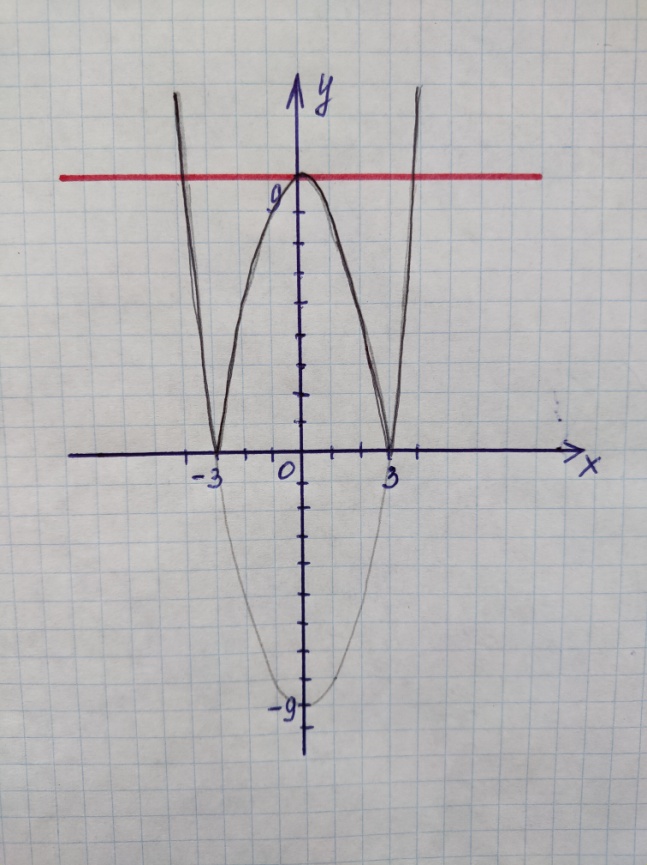 Постройте график функции
Постройте график функции 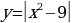 и определите, при каких значениях m прямая у = m пересекает график ровно в трёх точках.
и определите, при каких значениях m прямая у = m пересекает график ровно в трёх точках.
Решение:
П
Рис. 12
рименим результаты исследования № 1. Построим график функции
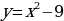
и ту часть графика, которая находится под осью ОХ, отобразим симметрично этой оси. Из рисунка видно, что прямая у = m, параллельная оси ОХ имеет с квадратичной функцией ровно три общие точки при m = 9.
Ответ: m = 9.
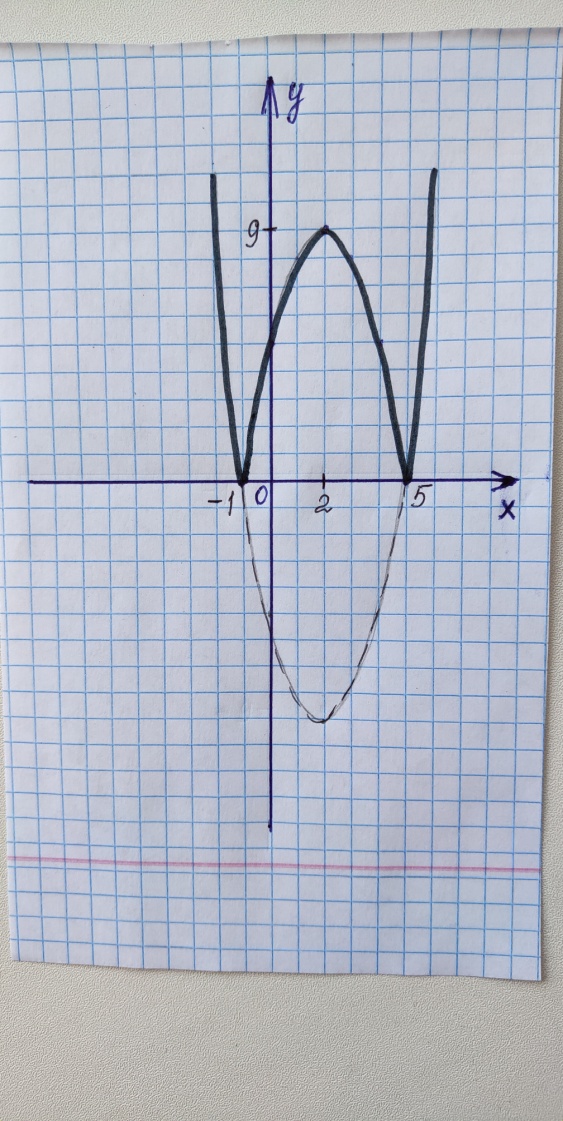
Постройте график функции 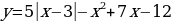 и определите, при каких значениях m прямая у = m имеет с графиком ровно три общие точки.
и определите, при каких значениях m прямая у = m имеет с графиком ровно три общие точки.
Решение:
Воспользуемся определением модуля и рассмотрим два случая:
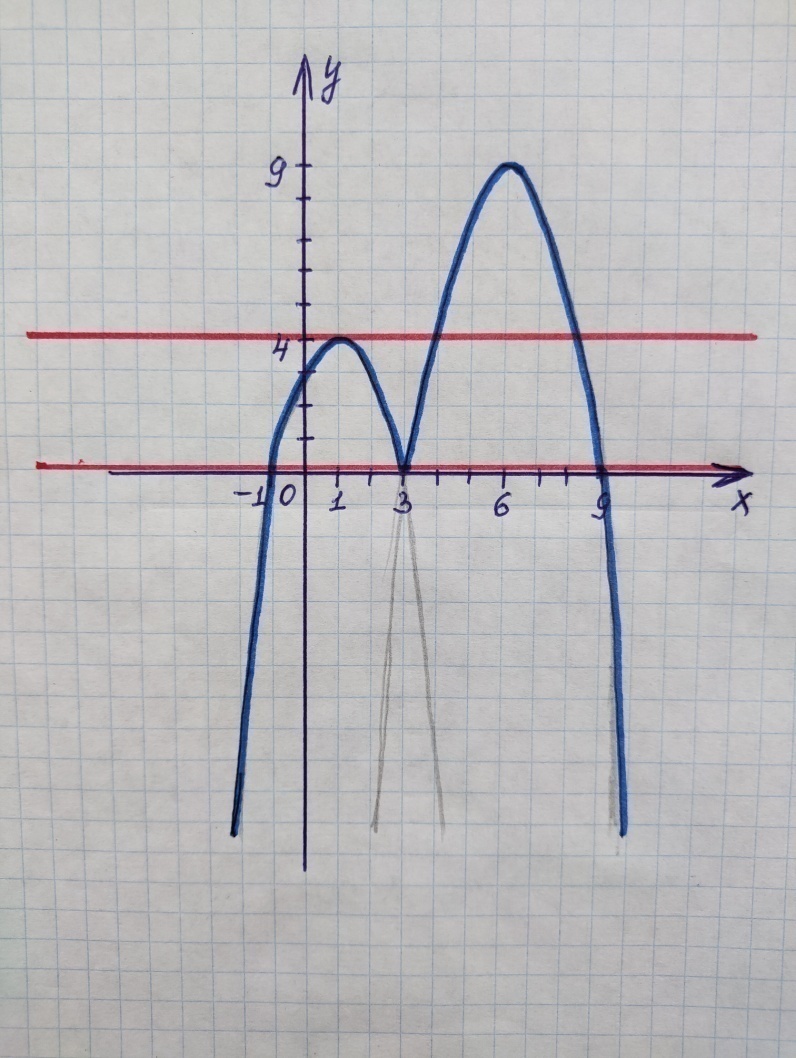
 , тогда функция примет вид
, тогда функция примет вид 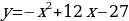 . Координата вершины (6; 9). Нули функции: х = 3; х = 9. Построим график данной функции и выделим ту часть графика, где
. Координата вершины (6; 9). Нули функции: х = 3; х = 9. Построим график данной функции и выделим ту часть графика, где 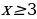 .
.
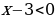 , тогда функция примет вид
, тогда функция примет вид 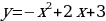 . Координата вершины (1; 4). Нули функции: х = -1; х = 3. Построим график данной функции и выделим ту часть графика, где
. Координата вершины (1; 4). Нули функции: х = -1; х = 3. Построим график данной функции и выделим ту часть графика, где 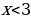 .
.
И
Рис. 13
з рисунка видно, что прямая у = m, параллельная оси ОХ имеет с квадратичной функцией ровно три общие точки при m = 4 и m = 0.
Ответ: m = 4 и m = 0.
Заключение.
Проводя исследования по построению квадратичной функции, содержащей модуль, ребята сделают вывод: местоположение абсолютной величины в квадратичной функции видоизменяет график, но в некоторых случаях повторяет его. Например, графики функций 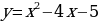 и
и 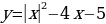 , совершенно одинаковы; одинаковы и
, совершенно одинаковы; одинаковы и 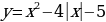 и
и 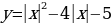 (его можно построить, если изобразить, ту часть графика, где
(его можно построить, если изобразить, ту часть графика, где  симметрично относительно оси ОУ). Для построения графика функции
симметрично относительно оси ОУ). Для построения графика функции 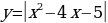 и
и 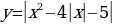 достаточно изобразить зеркально, ту часть, которая находится под осью ОХ. А
достаточно изобразить зеркально, ту часть, которая находится под осью ОХ. А 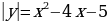 вообще не является функцией. Я уверена, что знания, которые ребята получат в процессе работы, помогут им при работе с другими функциями, содержащими модуль.
вообще не является функцией. Я уверена, что знания, которые ребята получат в процессе работы, помогут им при работе с другими функциями, содержащими модуль.
Литература.
Ю.Н. Макарычев, Н.Г., Миндюк, К.И. Нешков, С.Б. Суворова «Алгебра 9 класс», Москва, «Просвещение», 2014 г.
Т.Т. Баукова «Элективный курс. Знакомьтесь: модуль! Алгебра 8 – 9 классы», Волгоград, издательско – торговый дом «Корифей», 2007 г.
М.Л. Галицкий, А.М. Гольдман, Л.И. Звавич «Сборник задач по алгебре для 8 – 9 классов: Учеб. пособие для учащихся школы и классов с углубленным изучением математики» – 2 –е издание, Москва, Просвещение, 1994.
Г.В. Дорофеев «Математика. Алгебра. Функции. Анализ данных. 9 класс», Москва, «Дрофа», 2001г.
И.В. Ященко «ОГЭ математика», Москва, «Экзамен», 2018год.
Рисунки на yandex.ru
| Приложение 1. Парабола вокруг нас |
|  Ворота Сент – Луиса в Миссури. Ворота Сент – Луиса в Миссури.
|  Эйфелева башня в Париже. Эйфелева башня в Париже.
|
| Станция Киевская Кольцевой линии Московского метрополитена. 
| Каса Мила в Барселоне. |
|  Памятник оборонного зодчества Киевской Руси периода правления Ярослава Мудрого. Памятник оборонного зодчества Киевской Руси периода правления Ярослава Мудрого.
| Фонтан. 
|
|  Форма горного массива. Форма горного массива.
|  Радуга. Радуга.
|
|  Прыжок дельфина. Прыжок дельфина.
|  Берёза. Берёза.
|
| Приложение 2. |
| 
| 
|
| Роджер Котс. 
| 
|
| 
|







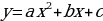 по алгоритму. Решая задачи ОГЭ под номером 23, я часто встречаю графики функций, содержащих модуль. Поэтому решила предложить учащимся выяснить, как будет выглядеть график параболы в зависимости от расположения знака модуля.
по алгоритму. Решая задачи ОГЭ под номером 23, я часто встречаю графики функций, содержащих модуль. Поэтому решила предложить учащимся выяснить, как будет выглядеть график параболы в зависимости от расположения знака модуля.
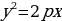 , где р=2OF. (Большой энциклопедический словарь, 2012)
, где р=2OF. (Большой энциклопедический словарь, 2012)
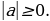
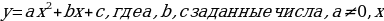 – независимая переменная, называется квадратичной функцией. Графиком квадратичной функции является кривая, называемая параболой. В уравнении квадратичной функции: а – старший коэффициент, b – второй коэффициент, с – свободный член.
– независимая переменная, называется квадратичной функцией. Графиком квадратичной функции является кривая, называемая параболой. В уравнении квадратичной функции: а – старший коэффициент, b – второй коэффициент, с – свободный член. 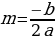 , ординату n можно найти, подставив найденное значение абсциссы в формулу
, ординату n можно найти, подставив найденное значение абсциссы в формулу 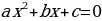 , корни уравнения - абсциссы точек пересечения с осью ОХ.
, корни уравнения - абсциссы точек пересечения с осью ОХ.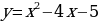 по алгоритму.
по алгоритму.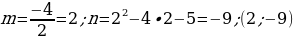
 ерез вершину параболы проведём ось симметрии параллельно оси ОУ.
ерез вершину параболы проведём ось симметрии параллельно оси ОУ.
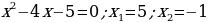
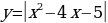 .
. Воспользуемся определением модуля и рассмотрим два случая:
Воспользуемся определением модуля и рассмотрим два случая: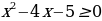 , тогда
, тогда 
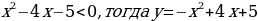 и выделим все точки с положительной ординатой
и выделим все точки с положительной ординатой 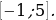
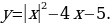
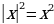 , то график функции
, то график функции 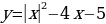 совпадает с графиком функции
совпадает с графиком функции 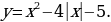
 Воспользуемся определением модуля и рассмотрим два случая:
Воспользуемся определением модуля и рассмотрим два случая: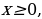 тогда
тогда 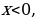 тогда
тогда 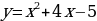 . Построим параболу
. Построим параболу 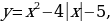 надо сохранить ту часть графика функции
надо сохранить ту часть графика функции  и симметрично отразить эту часть графика относительно оси ОУ.
и симметрично отразить эту часть графика относительно оси ОУ.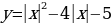 .
.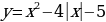 .
.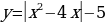 .
. Воспользуемся определением модуля и рассмотрим два случая:
Воспользуемся определением модуля и рассмотрим два случая: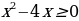 , построим график функции
, построим график функции 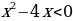 , построим график функции
, построим график функции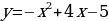 на интервале
на интервале 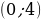 .
. 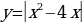 и опустить его на пять единиц вдоль оси ОУ.
и опустить его на пять единиц вдоль оси ОУ. 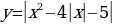 .
. Воспользуемся результатами проделанной работы и обратимся к исследованию № 1 и № 3. Тогда график функции
Воспользуемся результатами проделанной работы и обратимся к исследованию № 1 и № 3. Тогда график функции 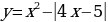 .
. Выясним, при каком значении х выражение, стоящее под знаком модуля, равно нулю:
Выясним, при каком значении х выражение, стоящее под знаком модуля, равно нулю: 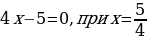 .
.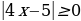 , при
, при 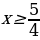 , тогда функция
, тогда функция 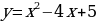 . Построим эту функцию на интервале
. Построим эту функцию на интервале  б
б 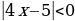 , при
, при 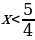 , тогда функция
, тогда функция 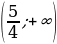 .
. 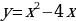 и поднять его на пять единиц вдоль оси ОУ (справа на рисунке), и если построить график функции
и поднять его на пять единиц вдоль оси ОУ (справа на рисунке), и если построить график функции 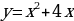 и опустить его на пять единиц вдоль оси ОУ (слева на рисунке).
и опустить его на пять единиц вдоль оси ОУ (слева на рисунке). 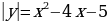 .
. М
М 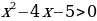 , получаем, что заданному значению х соответствует два значения у. Потому данная зависимость не является функцией. Раскроем модуль и построим график уравнения с двумя переменными. При
, получаем, что заданному значению х соответствует два значения у. Потому данная зависимость не является функцией. Раскроем модуль и построим график уравнения с двумя переменными. При 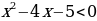 , получим
, получим 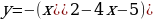 .
.  Постройте график функции
Постройте график функции 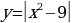 и определите, при каких значениях m прямая у = m пересекает график ровно в трёх точках.
и определите, при каких значениях m прямая у = m пересекает график ровно в трёх точках.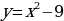 и ту часть графика, которая находится под осью ОХ, отобразим симметрично этой оси. Из рисунка видно, что прямая у = m, параллельная оси ОХ имеет с квадратичной функцией ровно три общие точки при m = 9. Ответ: m = 9.
и ту часть графика, которая находится под осью ОХ, отобразим симметрично этой оси. Из рисунка видно, что прямая у = m, параллельная оси ОХ имеет с квадратичной функцией ровно три общие точки при m = 9. Ответ: m = 9. 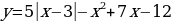 и определите, при каких значениях m прямая у = m имеет с графиком ровно три общие точки.
и определите, при каких значениях m прямая у = m имеет с графиком ровно три общие точки.
 , тогда функция примет вид
, тогда функция примет вид 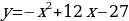 . Координата вершины (6; 9). Нули функции: х = 3; х = 9. Построим график данной функции и выделим ту часть графика, где
. Координата вершины (6; 9). Нули функции: х = 3; х = 9. Построим график данной функции и выделим ту часть графика, где 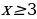 .
.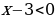 , тогда функция примет вид
, тогда функция примет вид 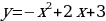 . Координата вершины (1; 4). Нули функции: х = -1; х = 3. Построим график данной функции и выделим ту часть графика, где
. Координата вершины (1; 4). Нули функции: х = -1; х = 3. Построим график данной функции и выделим ту часть графика, где 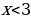 .
. Ворота Сент – Луиса в Миссури.
Ворота Сент – Луиса в Миссури. Эйфелева башня в Париже.
Эйфелева башня в Париже.

 Памятник оборонного зодчества Киевской Руси периода правления Ярослава Мудрого.
Памятник оборонного зодчества Киевской Руси периода правления Ярослава Мудрого. 
 Форма горного массива.
Форма горного массива. Радуга.
Радуга. Прыжок дельфина.
Прыжок дельфина. Берёза.
Берёза.













