Практическая работа по теме «Вычисление длины окружности и площади круга»

Практическая работа по теме «Вычисление длины окружности и площади круга»

Для формулировки цели, гипотезы и вывода учащимися на практических и лабораторных работах использую следующие приёмы:

-даю систему опорных вопросов, т.е. провожу актуализацию знаний;

-даю карточки-подсказки с пропущенными словами или числами или с пропущенной частью формулы;

-пишу в инструкции, о чём должна быть цель, гипотеза или вывод;

- использую карточки с дополнительными заданиями;

-перед выдвижением гипотезы даю предварительные задания по пройденным темам, проанализировав результаты которых можно вывести связь между рассматриваемыми величинами;

- перед выдвижением гипотезы задаю проблемный вопрос;

-при подведении итога урок, на котором выполнялась практическая или лабораторная работа использую приёмы: «синквейн», «лестница достижений», «балльная система оценивания» как способы проведения рефлексии.

На первых лабораторных и практических работах в 5 классе работа идёт по инструкции, которую даёт учитель. Инструкция содержит лишь этапы: тема, цель, оборудование, ход работы и вывод. Причём первые 3 этапа уже написаны. Ученики лишь заполняют ход работы по готовому алгоритму и записывают вывод, исходя из цели работы.

На практической работе по теме « Вычисление длины окружности и площади круга» в 6 классе предлагаю выполнить работу по готовому алгоритму.

В начале урока предлагаю детям систему вопросов, т.е. провожу актуализацию знаний.

1. Что такое – окружность?

2. Какой отрезок называется а) радиусом, б) диаметром окружности?

3. Что можно сказать о длине радиуса и длине диаметра?

4. Чем круг отличается от окружности?

5. Как на практике, не зная расчётной формулы, можно узнать значение длины окружности?

6. По каким формулам можно найти а) длину окружности, б) площадь круга?

7. Как округлить десятичную дробь до единиц, до десятых, до сотых?

Цель и оборудование пишу в инструкции сама.

Если работа обучающая цель должна начинаться со слов: я научусь… (или научиться)

Цель: научиться находить длину окружности и площадь круга по формулам, выполнив необходимые измерения и расчеты и обобщать результаты своей работы.

Оборудование: 3 модели круга разного радиуса, циркуль, масштабная линейка, нитка, ножницы, клей-карандаш.

Затем ученики выдвигают гипотезу.

Чтобы они смогли это сделать, использую следующие приёмы.

Пишу в инструкции, о чём должна быть гипотеза.

Например:Гипотеза: (О количественной связи длины окружности и её радиуса),

а более слабым ученикам раздаю карточки-подсказки с пропущенными словами или числами:

Гипотеза: длина окружности больше её радиуса примерно в ……. раз.

Гипотеза: (О том, как меняется длина окружности в зависимости от радиуса : если радиус увеличился (уменьшился) в k раз, то длина окружности………………в ………..раз)

Затем ученикам раздаю инструкции для выполнения работы, и ученики, используя её, записывают в тетради ход работы, выполнив необходимые измерения и написав необходимые расчётные формулы.

В алгоритме выполнения работы использую систему незаконченных предложений (в которых, например, нужно дописать правую часть формулы). Например:

• Провожу и измеряю радиус 1-ой окружности (в мм): R1 =

• Вычисляю по формуле C1 = -------- длину 1-ой окружности , округлив значение числа «пи» до десятых: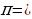

• Записываю решение:

• Записываю ответ:

Затем ученики проверяют гипотезу, анализируя результаты.

В конце урока предлагаю ученикам обобщить результаты работы. На этом этапе применяю дифференцированный подход. Более мотивированным ученикам предлагаю сделать выводы самим. А слабым ученикам даю карточки-подсказки с пропущенными словами или указываю в инструкции, о чём должен быть сделан вывод.

Например:

Вывод-1: ( о том, как меняется длина окружности в зависимости от радиуса ( если радиус увеличился (уменьшился) в ….. раз, то длина окружности……………… )

Вывод- 2: (выявляю закономерность: длина окружности больше её радиуса примерно в … раз)

Вывод по окончании работы: (о том чему научился на практической работе и как найти длину окружности и площадь круга, зная радиус).

А если практическую или лабораторную работу дети выполняют индивидуально, то составляю дифференцированные инструкции с заданиями разной степени сложности.