Дисциплина – «Теория вероятностей»
Курс -3
Занятие - 36
Практическая работа № 17 Тема:
«Показательный закон распределения. Решение задач»
Методические указания
Цель:
закрепление знаний о непрерывных случайных величинах,
формирование умений составлять функции распределения вероятностей и функции плотности вероятностей НСВ, распределенной по показательному закону,
формирование умений вычислять вероятности по экспоненциальному закону,
формирование ОК 2,3,4,6,7, ПК 1.1
ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.
ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.
ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями.
ОК 7. Брать на себя ответственность за работу членов команды (подчиненных), результат выполнения заданий.
ПК 1.1. Собирать данные для анализа использования и функционирования информационной системы, участвовать в составлении отчетной документации, принимать участие в разработке проектной документации на модификацию информационной системы.
Теоретический материал и методические указания
Показательное распределение
Плотность распределения показательно распределенной величины
Функция распределения показательно распределенной величины
Числовые характеристики показательно распределенной величины: математическое ожидание, дисперсия, среднее квадратическое отклонение.
Решения типовых задач по теме
Случайная величина X распределена по экспоненциальному закону с параметром 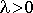 Если ее плотность распределения вероятностей задается формулой:
Если ее плотность распределения вероятностей задается формулой:
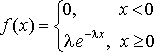 (1)
(1)
Функция распределения показательного закона:
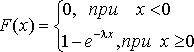 (2)
(2)
Пример 1. Время безотказной работы ЭВМ – случайная величина Х, имеющая показательное распределение с параметром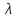 = 5 (физический смысл величины
= 5 (физический смысл величины 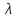 - среднее число отказов в единицу времени, не считая простоев ЭВМ для ремонта). Известно, что ЭВМ уже проработала без отказов время х. Найти при этих условиях плотность и функцию распределения времени, которое проработает ЭВМ после момента х до ближайшего отказа.
- среднее число отказов в единицу времени, не считая простоев ЭВМ для ремонта). Известно, что ЭВМ уже проработала без отказов время х. Найти при этих условиях плотность и функцию распределения времени, которое проработает ЭВМ после момента х до ближайшего отказа.
Решение. Так как простейший поток отказов не имеет последствия, вероятность появления хотя бы одного отказа на участке от х до х + х0 не зависит от того, появлялись ли отказы ранее момента х. Следовательно, подставив 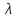 = 5 в формулы (1) и в (2), получим:
= 5 в формулы (1) и в (2), получим:
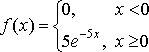 .
.
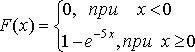 .
.
Вероятность попадания в интервал 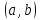 случайной величины X, распределенной по показательному закону
случайной величины X, распределенной по показательному закону 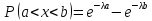 .
.
Показательным законом надежности называют функцию надежности, определяемую равенством
R(t) = e-λt , (3)
где λ – интенсивность отказов.
Пример 2. Пусть время безотказной работы элемента распределено по показательному закону с плотностью распределения f(t) = 0,1 e-0,1t при t ≥ 0. Найти вероятность того, что элемент проработает безотказно в течение 10 часов.
Решение. Так как λ = 0,1, R(10) = e-0,1·10 = e-1 = 0,368.
Дисциплина – «Теория вероятностей»
Курс -3
Занятие - 36
Практическая работа №17
Тема:
«Показательный закон распределения. Решение задач»
Задача 1. Написать плотность распределения вероятностей и функцию распределения случайной величины X, распределенной по показательному закону, если:
а) параметр 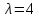 ; б) параметр
; б) параметр 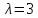 .
.
Задача 2. Случайная величина X распределена по показательному закону, причем
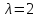 Найти вероятность попадания случайной величины Х в интервал:
Найти вероятность попадания случайной величины Х в интервал:
а) (0; 1); б) (2; 4).
Задание № 3. Найти М(Х), D(X), 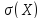 показательного закона распределения случайной величины X заданной функцией распределения:
показательного закона распределения случайной величины X заданной функцией распределения:
Найти плотность распределения вероятностей случайной величины X.
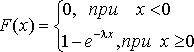
а) параметр 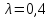 ; б) параметр
; б) параметр 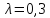 .
.
Задача 4. Испытываются два независимо работающих элемента. Длительность безотказной работы первого имеет показательное распределение 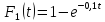 , второго -
, второго - 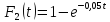 . Найти вероятность того, что за время длительностью 20 часов: а) оба элемента будут работать; б) откажет только один элемент.
. Найти вероятность того, что за время длительностью 20 часов: а) оба элемента будут работать; б) откажет только один элемент.
Задача 5. Случайная величина Х – время работы электролампочки имеет показательное распределение. Определить вероятность того, что время работы лампочки будет не меньше 900 часов, если среднее время работы лампочки:
а) 800 часов; б) 600 часов.
Задача 6. Вероятность безотказной работы элемента телевизора распределена по показательному закону 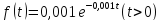 . Найти вероятность того, что телевизор проработает:
. Найти вероятность того, что телевизор проработает:
а) 1000 часов; б) 1500 часов.
Задача 7. Длительность безотказной работы элемента имеет показательное распределение
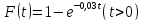 . Найти вероятность того, что за t=24 ч элемент:
. Найти вероятность того, что за t=24 ч элемент:
а) откажет; б) не откажет.





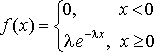 (1)
(1)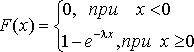 (2)
(2)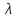 = 5 (физический смысл величины
= 5 (физический смысл величины 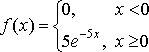 .
.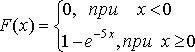 .
.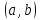 случайной величины X, распределенной по показательному закону
случайной величины X, распределенной по показательному закону 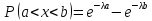 .
.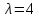 ; б) параметр
; б) параметр 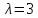 .
.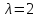 Найти вероятность попадания случайной величины Х в интервал:
Найти вероятность попадания случайной величины Х в интервал: 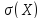 показательного закона распределения случайной величины X заданной функцией распределения:
показательного закона распределения случайной величины X заданной функцией распределения: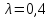 ; б) параметр
; б) параметр 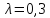 .
.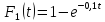 , второго -
, второго - 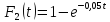 . Найти вероятность того, что за время длительностью 20 часов: а) оба элемента будут работать; б) откажет только один элемент.
. Найти вероятность того, что за время длительностью 20 часов: а) оба элемента будут работать; б) откажет только один элемент.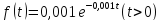 . Найти вероятность того, что телевизор проработает:
. Найти вероятность того, что телевизор проработает: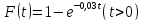 . Найти вероятность того, что за t=24 ч элемент:
. Найти вероятность того, что за t=24 ч элемент:









