Моделирование экономических задач. Оптимизация в OpenOffice Calc.
------------------------------------------------------------------------------------------------------------------------------------------
ПРАКТИЧЕСКАЯ РАБОТА
Задачи оптимизации некоторых процессов.
Цель работы: Изучение специальных возможностей электронных таблиц для решения оптимизационных задач и научиться создавать компьютерную модель для решения таких задач.
Постановка задачи1(из статьи, Н.С.Порываев «Уроки по решению экономических задач оптимизации различными средствами», Информатика в школе,№3,2013)
Мебельная фабрика выпускает кресла двух типов. На изготовление кресла первого типа расходуется 2 м досок стандартного сечения, 0,8 м2 обивочной ткани и затрачивается 2 человеко-часа, а на изготовление кресла второго типа соответственно 4 м, 1,25 м2 и 1,75 человеко-часа. Известно, что цена одного кресла первого типа равна 15 руб., второго типа – 20 руб. Сколько кресел каждого типа надо выпускать, чтобы стоимость выпускаемой продукции была максимальной, если фабрика имеет в наличии 4400 м досок, 1500 м2 обивочной ткани и может затратить 3200 человеко-часов рабочего времени на изготовление этой продукции?
Математическая модель задачи.
Среди целочисленных решений системы линейных неравенств:
2х + 4y
0,8x + 1?25y
2x + 1,75y
x=0; y=0
найти такое, при котором достигается максимум линейной функции
F(x,y)=15x + 20y
Ход решения:
Заполним расчетную форму в табличном процессоре OpenOfficeCalc.
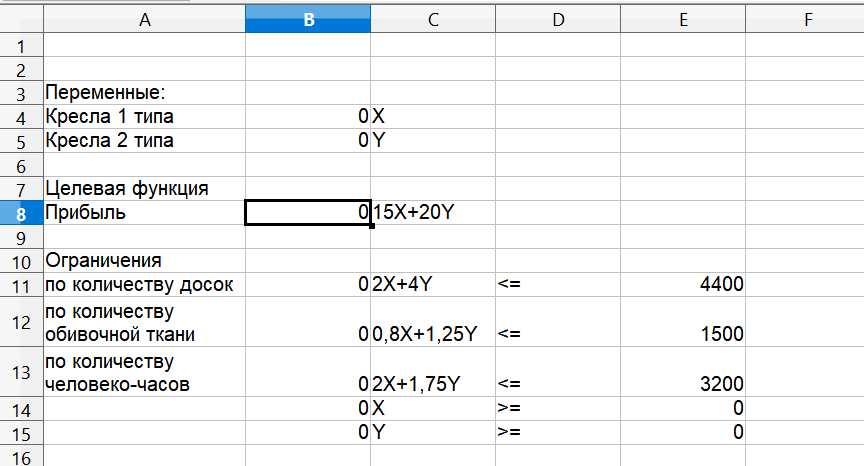
В ячейку В8 вставляем формулу =15*Х + 20*Y;
В ячейку В11 вставляем формулу =2*Х + 4*Y и так далее.
После заполнения ячеек выбираем пункт меню Сервис/Решатель.
Заполняем ячейки , как представлено на рисунке.
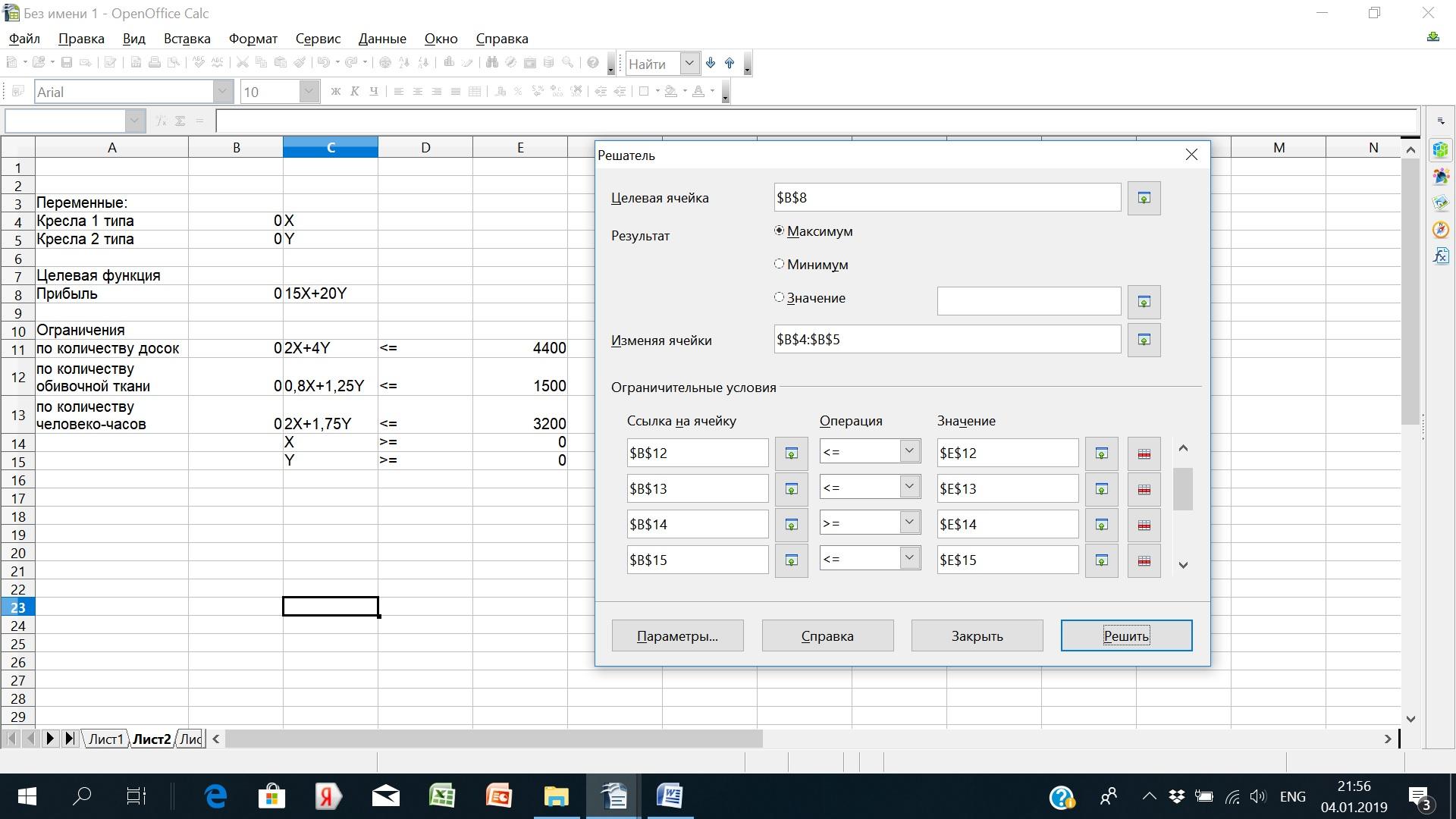
После заполнения всех данных, нажать на кнопку Решатель, должны получиться получим следующие данные.
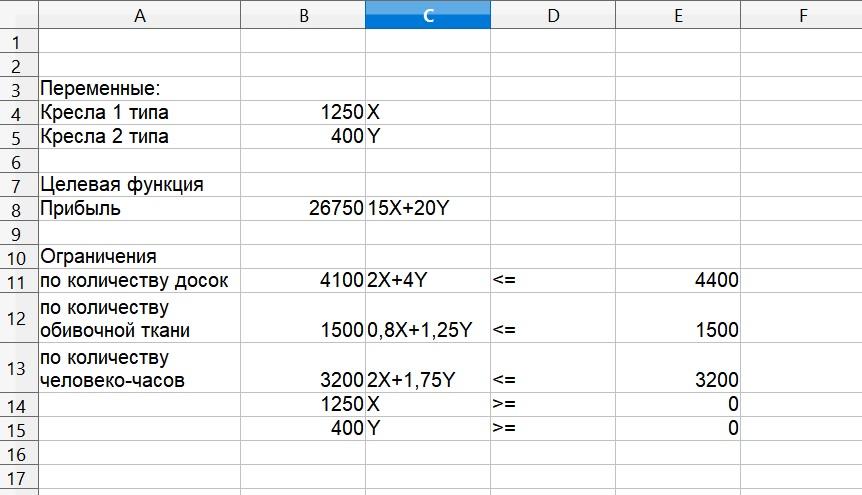
Измените значения- количества досок и количество обивочной ткани согласно таблице и оформить в виде отчета:
Отчет по практической работе «Задачи оптимизации с помощью специальных возможностей табличного процессора»
| Количество досок | Количество обивочной ткани | РЕЗУЛЬТАТ |
| X- количество кресел 1 типа | Y- количество кресел 2 типа | Целевая функция-Стоимость |
| 4400 | 1500 |
|
|
|
| 4000 | 1000 |
|
|
|
| 5000 | 2000 |
|
|
|
| произвольный | произвольный |
|
|
|
Постановка задачи 2 (оптимизация перевозок, Карасева Т.В. «Сборник задач и упражнений», стр.113)
Разработать проект, в котором будем строить компьютерную модель для следующей задачи: «В городе имеется 2 склада муки и два хлебзавода. Ежедневно с первого склада вывозится 50 т. муки, со второго — 70 т.. Эта мука доставляется на хлебзаводы, причем первый получает 40 т., второй — 80 т.
Допустим, что перевозки одной тонны муки с 1 склада на I хлебзавод обходиться в 120 руб., с 1 склада на II хлебзавод - 160 руб., со 2 склада на I хлебзавод - 80 руб., со 2 склада на II хлебзавод - 100 руб
Как нужно спланировать перевозки, чтобы стоимость была минимальной?
Модель будем строить используя некоторые специальные возможности табличного процессора:
АЛГОРИТМ РЕШЕНИЯ:
Введем следующие обозначения:
X1 – количество муки, которое нужно перевести с 1 склада на I завод.
X2 – количество муки, которое нужно перевести с 1 склада на II завод.
Y1 – количество муки, которое нужно перевести со 2 склада на I завод.
Y2 – количество муки, которое нужно перевести со 2 склада на II завод.
Запишем все известные условия в виде уравнений:
X1+X2 = 50
Y1 + Y2 = 70
Х1+Y1 = 40
Х2 + Y2 =80
Общая стоимость перевозок составляет:
F = 120*X1 + 160 *X2 + 80 * Y1 + 100* Y2
Задача, найти такие значения переменных X1,X2,Y1,Y2, чтобы значение функции F было минимальным.
Порядок выполнения:
В таблице запишем начальные значения:
X1=0; X2=50-X1;
Y1=0; Y2=70-Y1.
2.Наберем ограничения:
Х1+Y1 = 40
Х2 + Y2 =80
и целевую функцию:
= 120*X1 + 160 *X2 + 80 * Y1 + 100* Y2
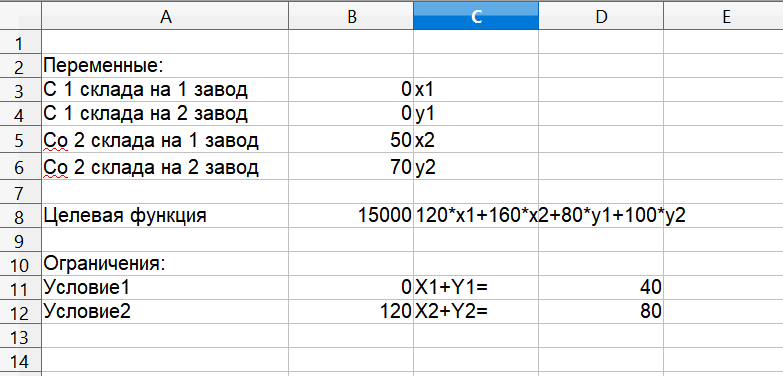
3.Наберем параметры для Решителя.
В результате получим результат:
X1=40; X2=10;
Y1=0; Y2=70;
F = 13400.
4. Результат показать преподавателю
Задача на дом:
«Ателье шьет женские юбки и платья из ткани двух видов. На одну юбку расходуется ткани первого вида 1,5 м2, второго – 0,5 м2, а на пошив одного платья расходуется ткани первого вида 1,6 м2, второго – 0,8 м2. Сколько платьев и юбок нужно сшить, чтобы добиться наибольшего дохода, если на складе имеется ткани первого аида 141 м2, а второго вида – 63 м2?
При этом известно, что доход мастерской от реализации одного платья составляет 10 у.е., а одной юбки – 6 у.е.
Необходимо: 1. Составить математическую модель задачи.
Решить задачу на компьютере.
Решить задачу с новыми ограничениями- со склада выдали тканей первого вида 120 м2.
Сделать вывод.































