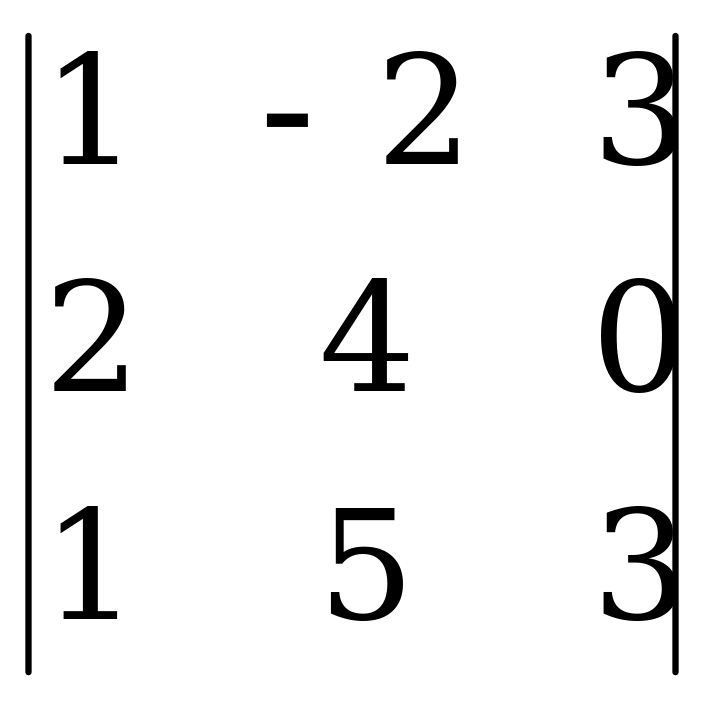Практическая работа
-
Название темы: «Вычисление определителей 2 и 3 порядка»
-
Учебные цели: отработать навыки решения определителя второго и третьего порядка
-
Продолжительность занятия: 2 часа.
-
Оснащение: методические указания для проведения практических занятий, тетради для практических работ.
-
Методические указания по выполнению работы: изучить краткие теоретические и учебно-методические материалы по теме практического занятия, изучить условие задания практического занятия; при выполнении работы соблюдать последовательность действий; ответить на контрольные вопросы; оформить отчет в тетради для практических работ.
-
Порядок выполнения работы:
1.1.ПРАВИЛО ПРЯМОУГОЛЬНИКА
Для вычисления определителя надо повторить запись первого и второго столбцов. Проведем три левые диагонали, начиная с верхнего левого угла, и три правые диагонали. Три первые слагаемые получаются как результат произведения элементов, стоящих на каждой из левых диагоналей. Следующие три слагаемые получаются при умножении элементов, стоящих на каждой из правых диагоналей. Три последние произведения берутся с противоположным знаком.
Пример 1
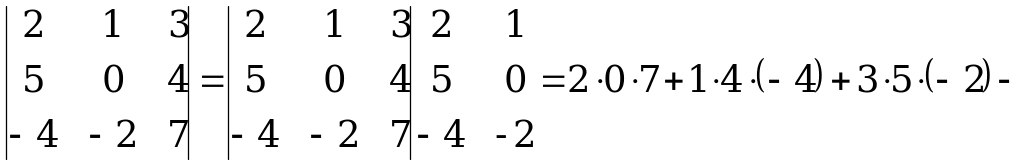






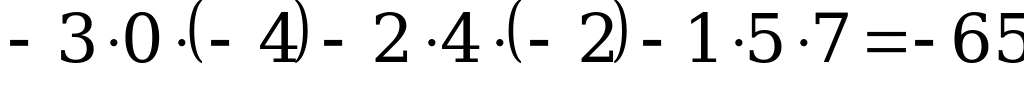 .
.
1.2. ПРАВИЛО ТРЕУГОЛЬНИКА
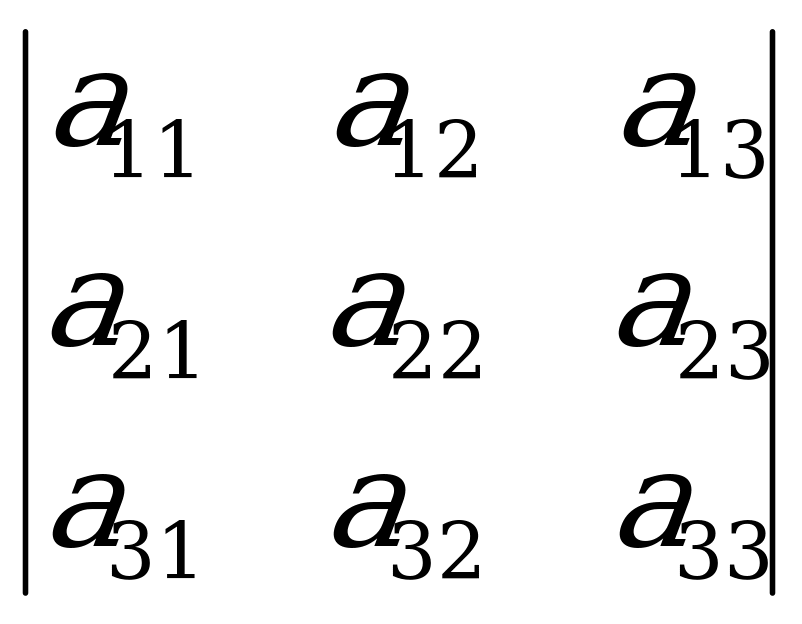
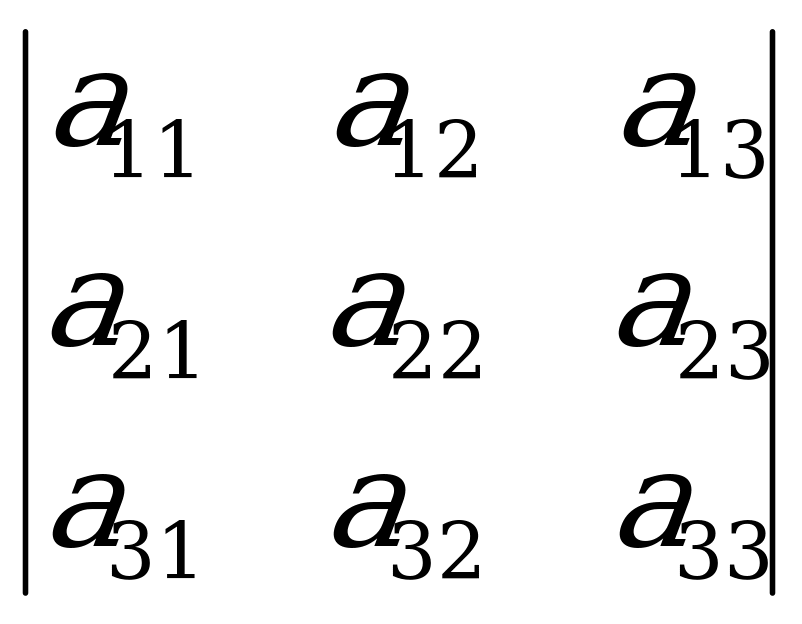


(1) (2)
Перемножаются элементы, стоящие на левых диагоналях. Одна диагональ, главная, проходит через три элемента, и две диагонали побочные проходят через два элемента, третьим элементом для них является элемент, стоящий в вершине треугольника (схема 1). Аналогично находим произведения элементов, стоящих на правых диагоналях (схема 2). Эти произведения берутся с обратным знаком.
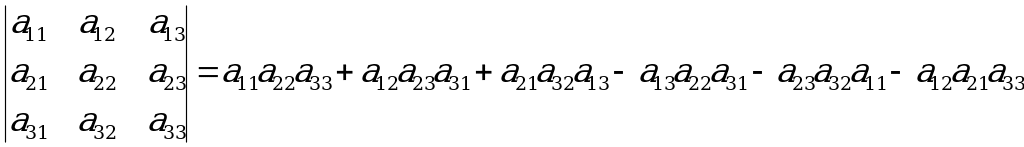 .
.
Пример 2
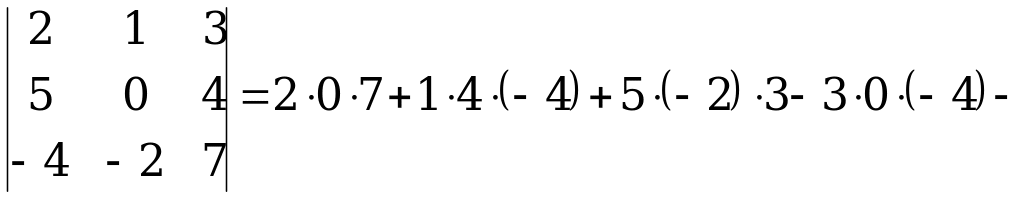
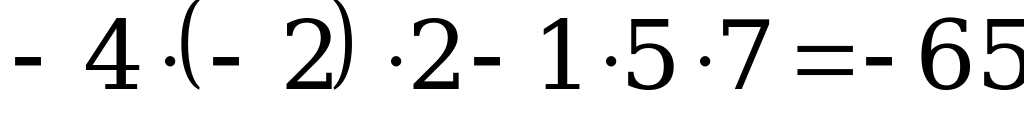 .
.
2. ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЯ ПУТЕМ РАЗЛОЖЕНИЯ
ПО ЭЛЕМЕНТАМ СТРОКИ
Прежде чем перейти к следующему правилу вычисления определителя, введем понятие минора и алгебраического дополнения. В определителе
 =
=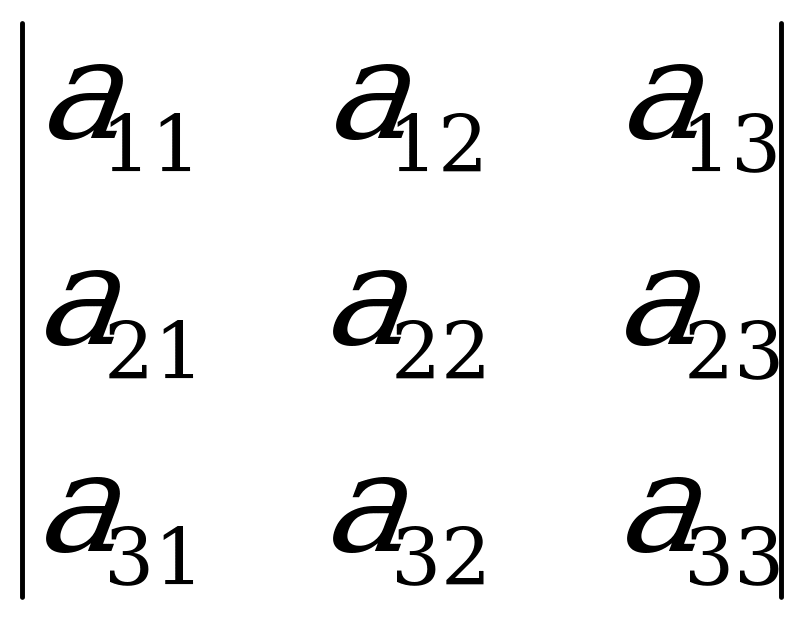
вычеркнем одну строку и один столбец, останется определитель второго порядка, который принято называть минором. Например, при вычеркивании первой строки и первого столбца получим минор
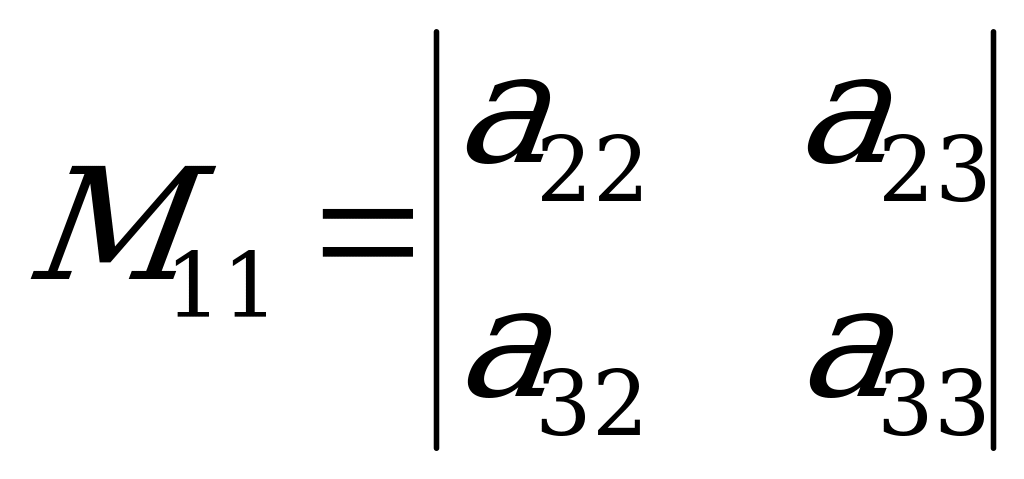 .
.
При вычеркивании “i”-й строки и “j”-го столбца получим минор 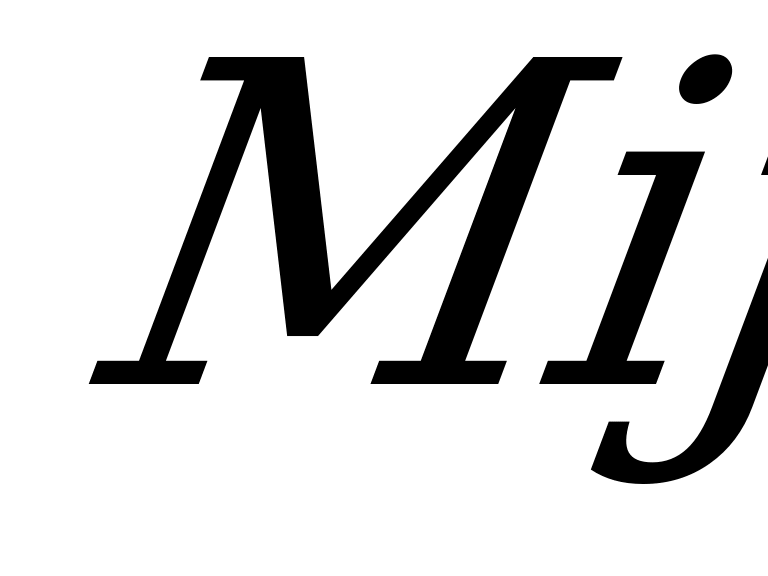 . Через
. Через  обозначим алгебраическое дополнение элемента
обозначим алгебраическое дополнение элемента  . Алгебраическим дополнением элемента
. Алгебраическим дополнением элемента определителя называется его минор, взятый со знакос «плюс», если сумма i+j - четное число, и со знаком «минус» если эта сумма нечетная т.е.
определителя называется его минор, взятый со знакос «плюс», если сумма i+j - четное число, и со знаком «минус» если эта сумма нечетная т.е.
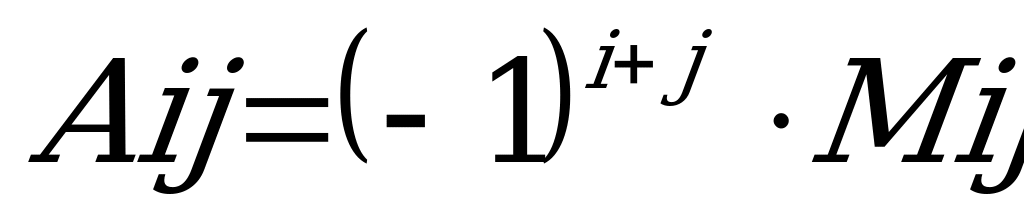 .
.
По свойствам определителя его можно представить в виде суммы:
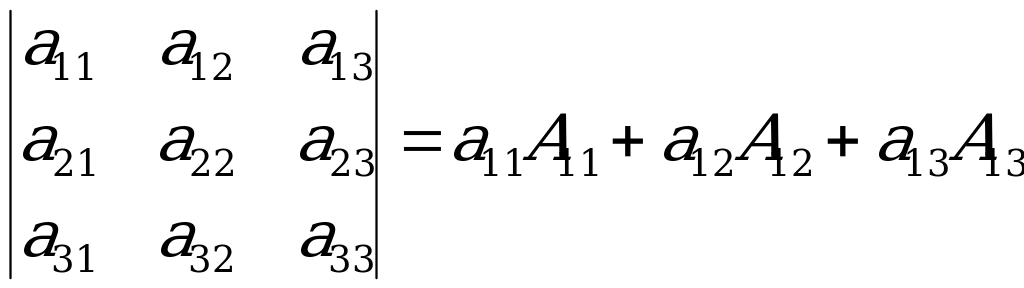 ,
,
что соответствует разложению определителя по элементам первой строки. Аналогично можно разложить по элементам любой строки или столбца.
Пример 3
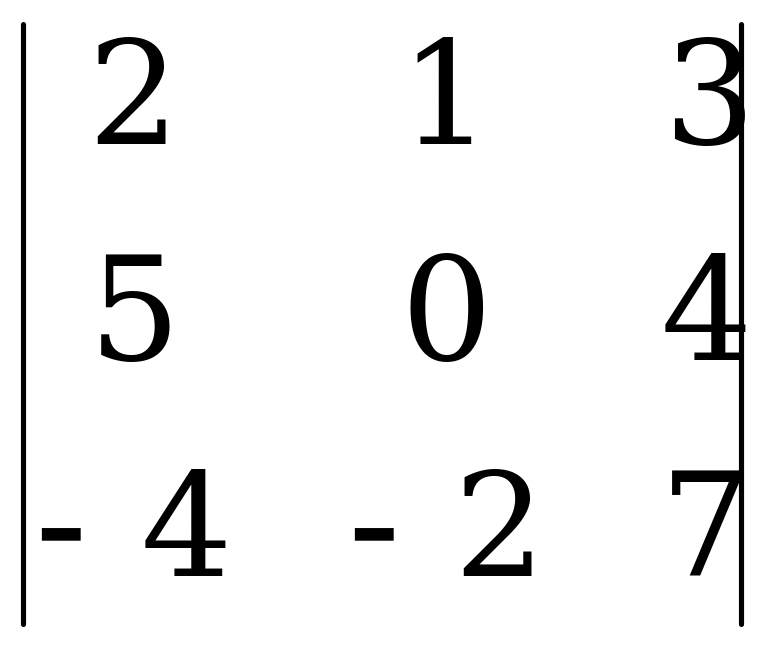 .
.
Вычислим определитель разложением по элементам строки. Для определенности выберем первую строку.
Тогда 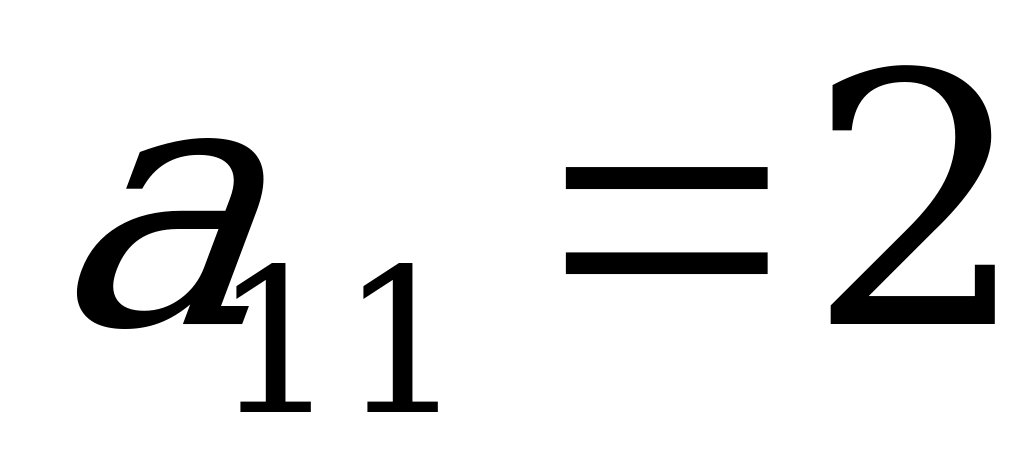 ,
, 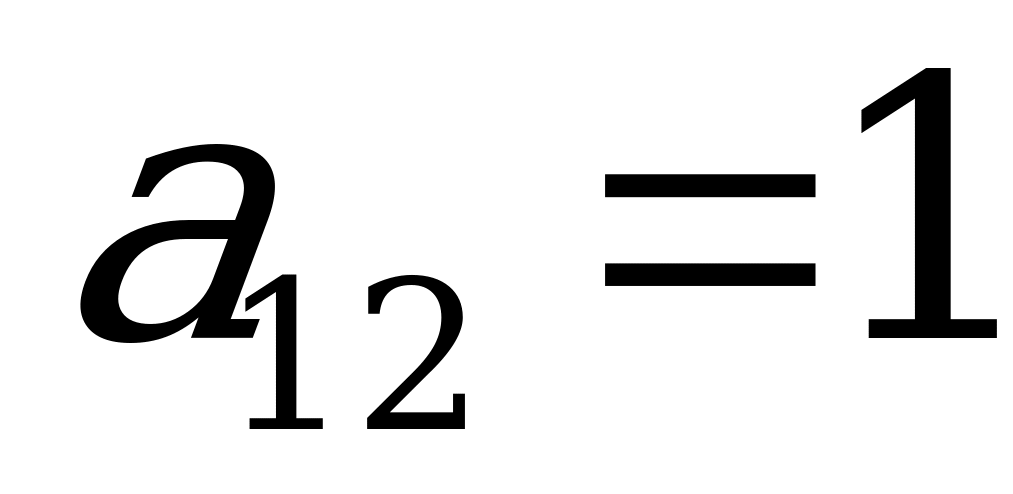 ,
, 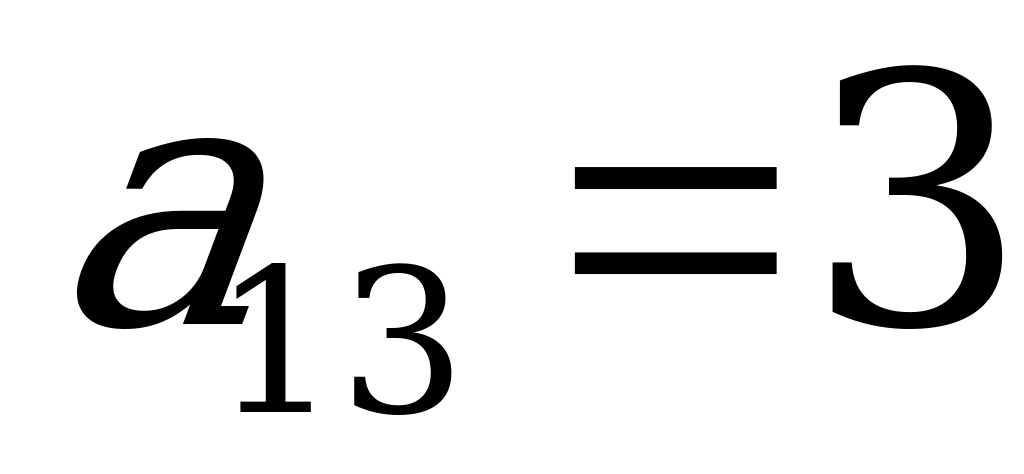 .
.
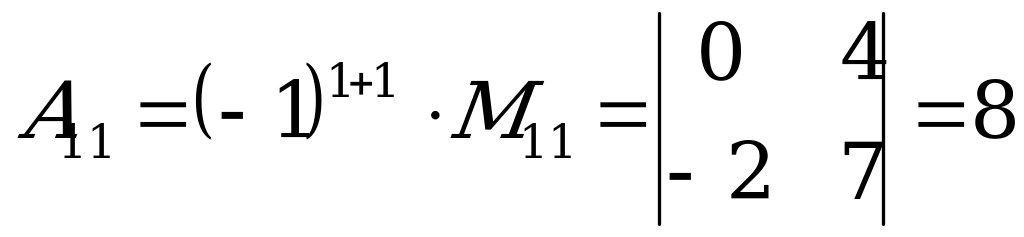 .
.
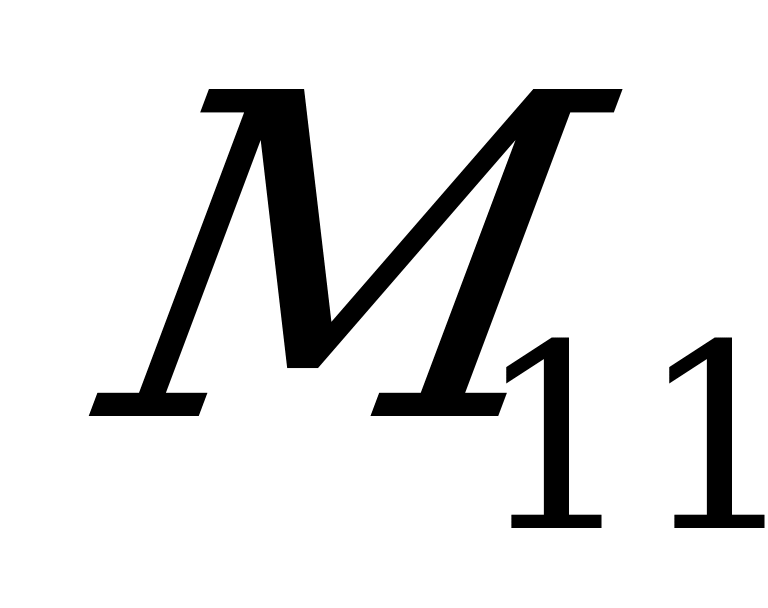 – получен вычеркиванием первой строки и первого столбца.
– получен вычеркиванием первой строки и первого столбца.
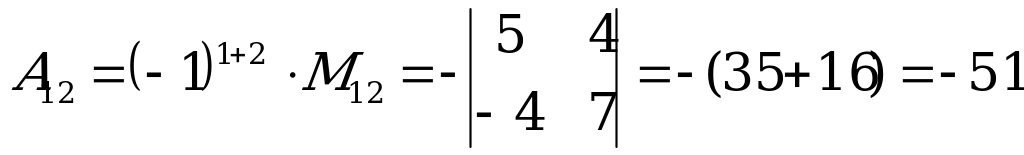 .
.
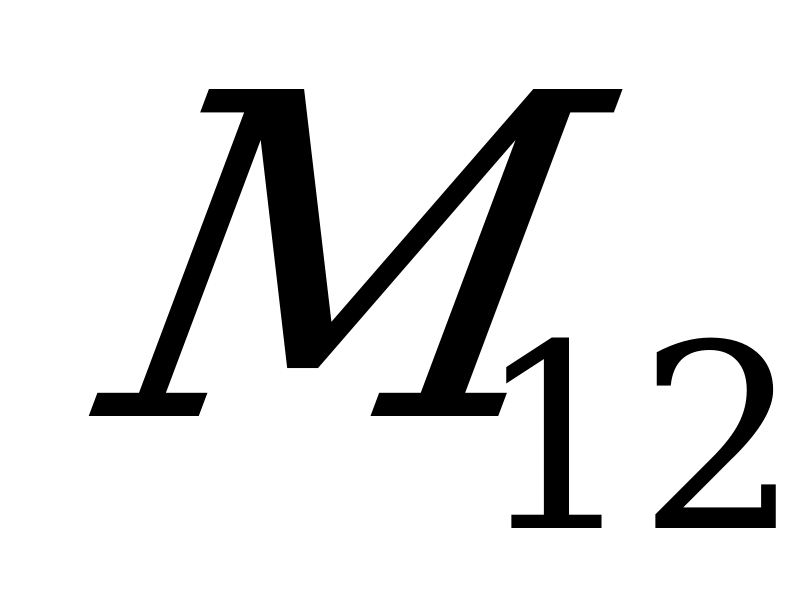 – получен вычеркиванием первой строки и второго столбца.
– получен вычеркиванием первой строки и второго столбца.
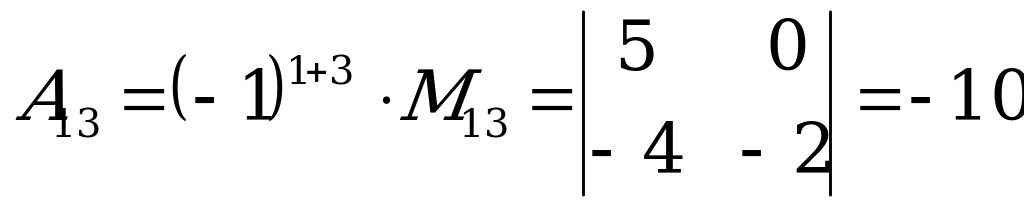 .
.
Тогда 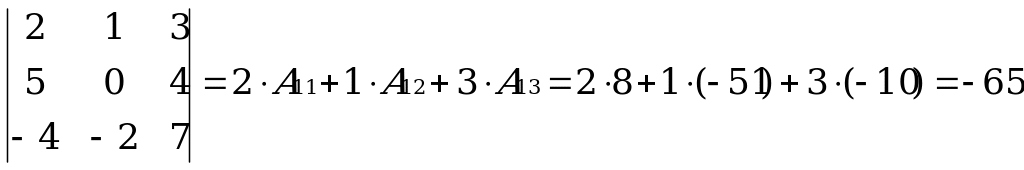 .
.
Вывод: Вычисление определителей. Определитель матрицы A размера 2x2 (определитель 2-го порядка) – это число, которое можно найти по правилу:
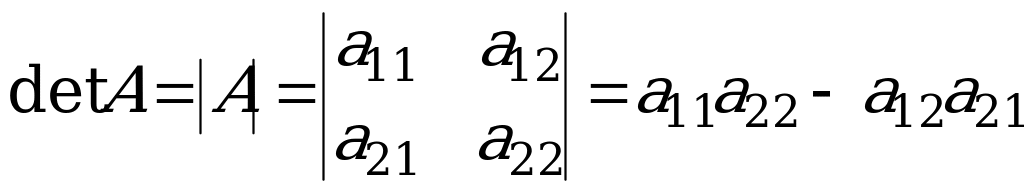
(произведение элементов, стоящих на главной диагонали матрицы, минус произведение элементов, стоящих на побочной диагонали).
Определитель матрицы A размера 3x3 (определитель 3-го порядка) – число, вычисляемое по правилу «раскрытие определителя по первой строке»:
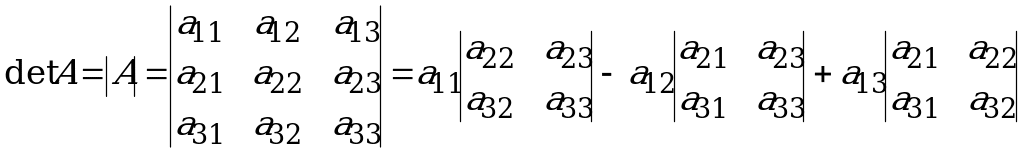
Пример 4
Найти: 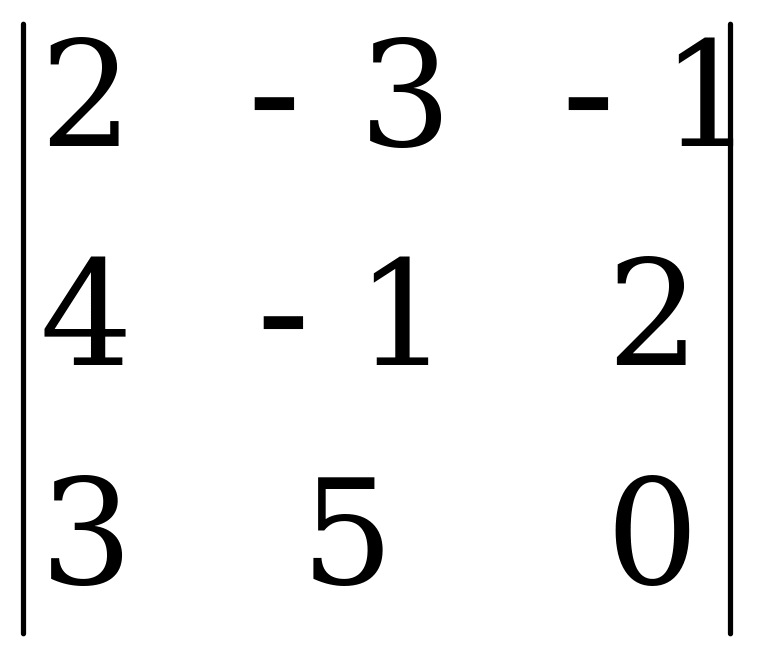
Решение:
При нахождении определителя воспользуемся сначала формулой 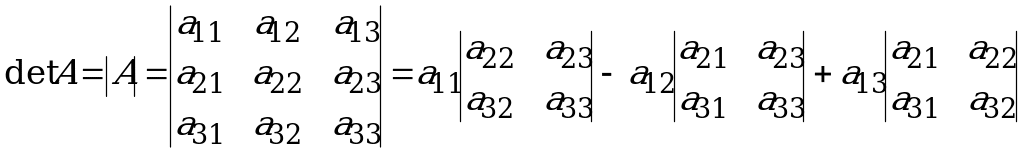 ,а затем (для вычисления определителей 2-го порядка) формулой
,а затем (для вычисления определителей 2-го порядка) формулой 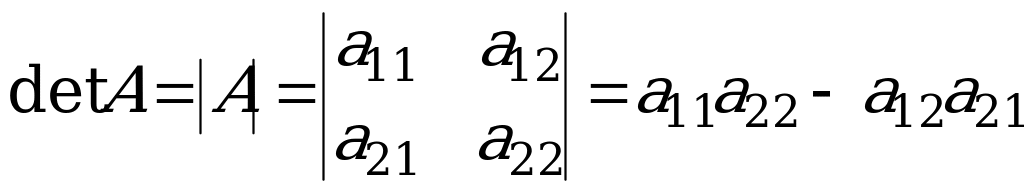 .
.
Задания:
Вычислите определители 3-го порядка:
а)  б)
б)  в)
в)  г)
г) 
д)  е)
е) 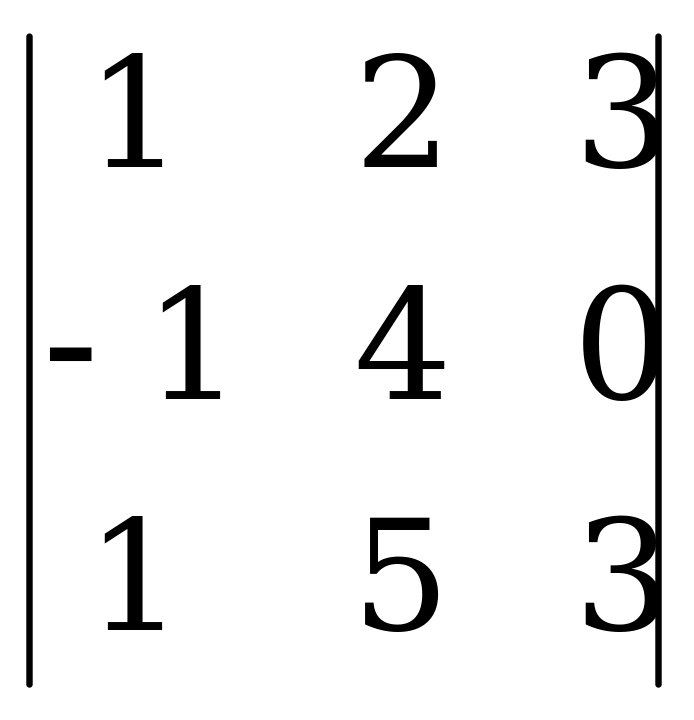 ж)
ж) 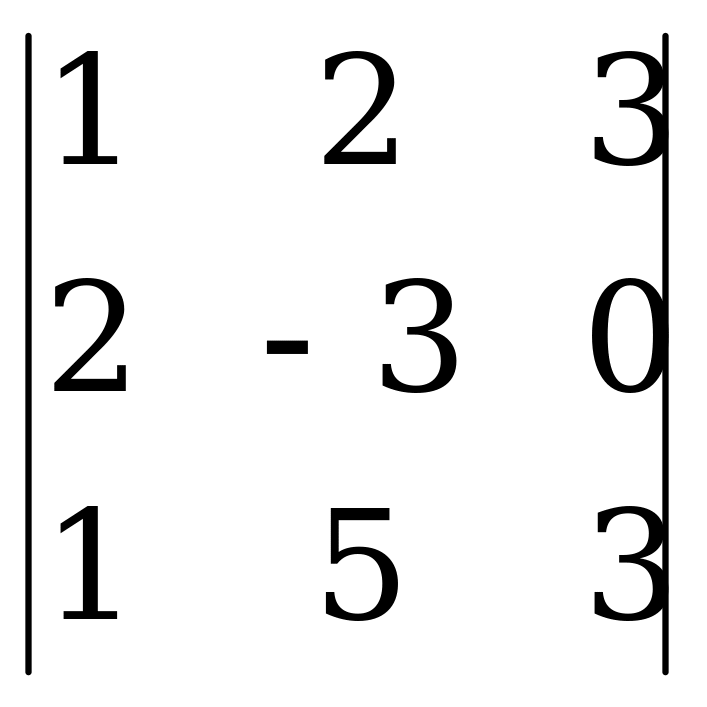 з)
з) 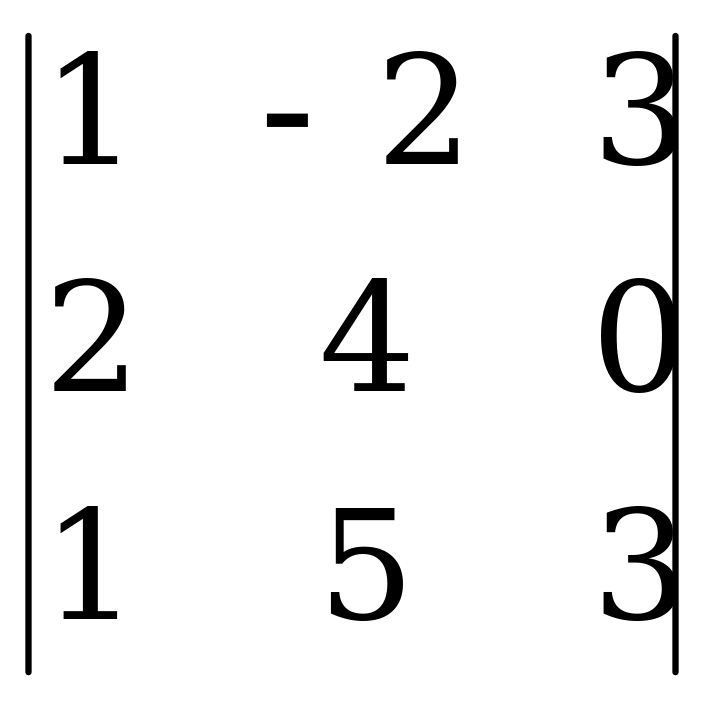
Контрольные вопросы
-
Что такое минор?
-
Что такое алгебраическим дополнением?
7.Форма отчета: выполнение заданий в тетради для практических работ.
8. Место проведения самоподготовки: читальный зал библиотеки.
9. Литература:
1. Попов, А.М. Информатика и математика: учебник и практикум для СПО / А.М. Попов, В.Н. Сотников, Е.И. Нагаева, М.Л. Акимов; под ред. А.М. Попова. – 2-е изд., перераб.и доп. – М.: Юрайт, 2020. – 509 с. – Проф. образование.
2. Шипачев, В.С. Математика: учебник и практикум для СПО / В.С. Шипачев; под ред. А.Н. Тихонова. – 8-е изд., перераб. и доп. – М.: Юрайт, 2020. – 447 с. – Проф. образование.






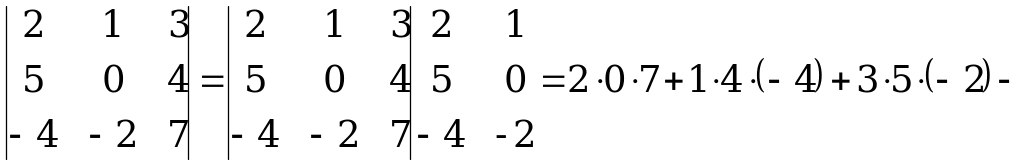


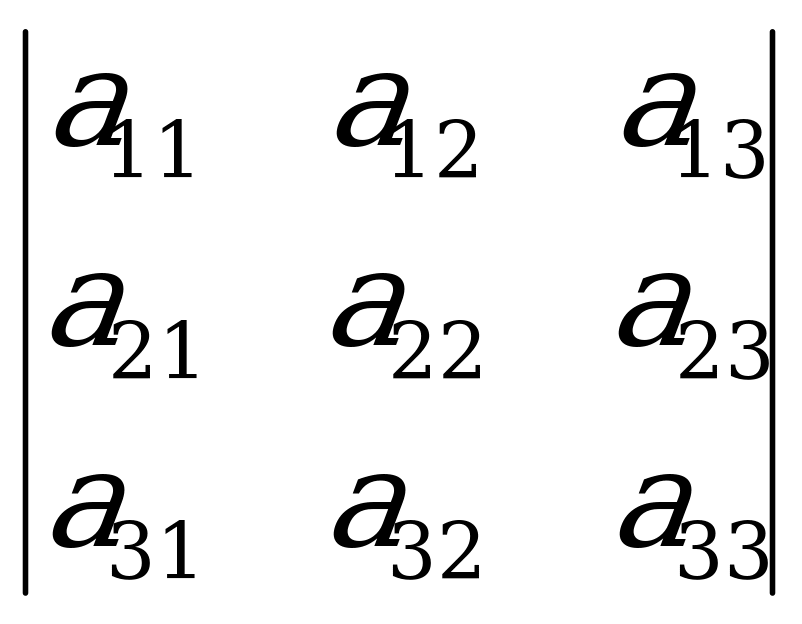


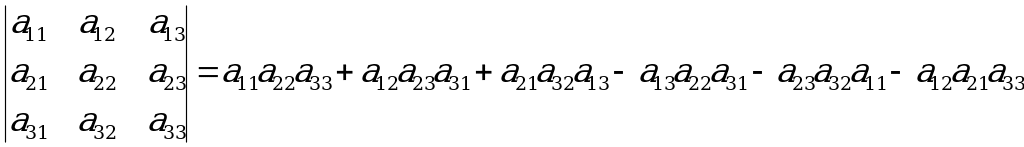 .
.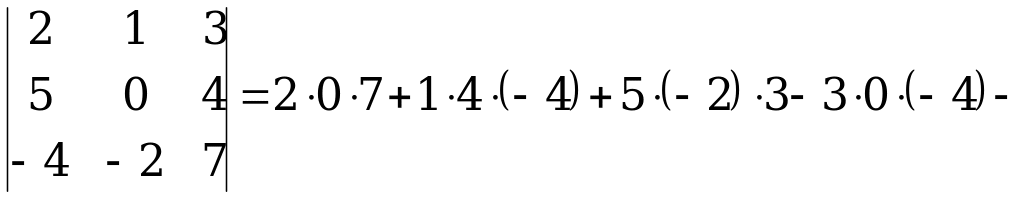
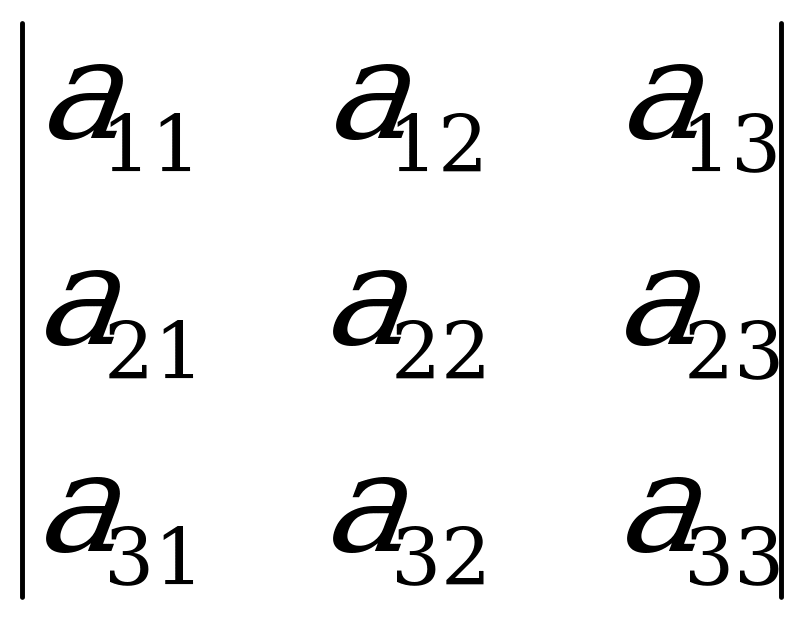
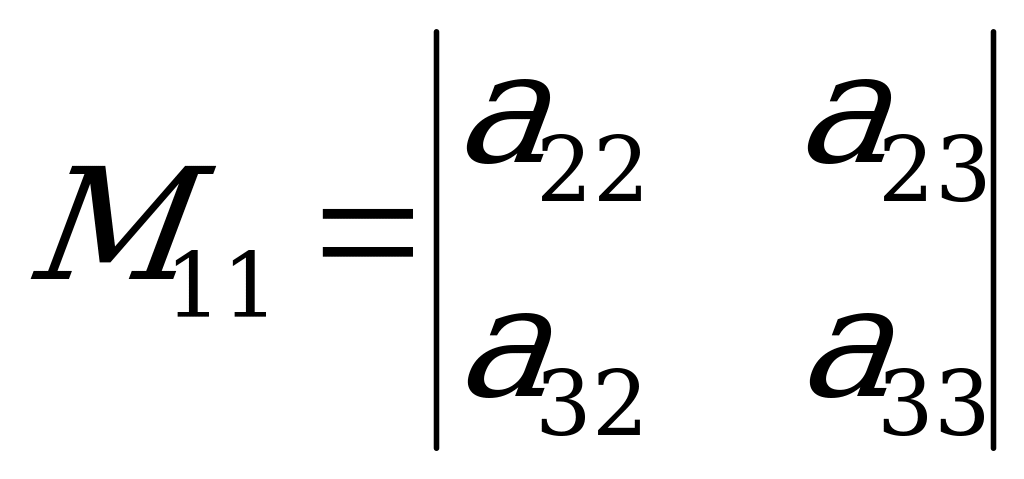 .
.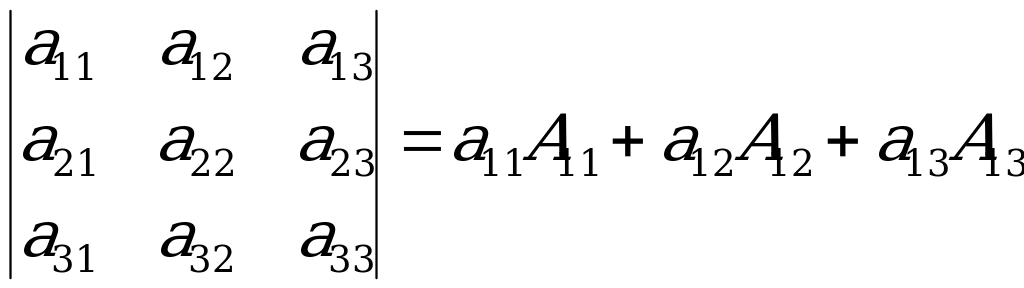 ,
,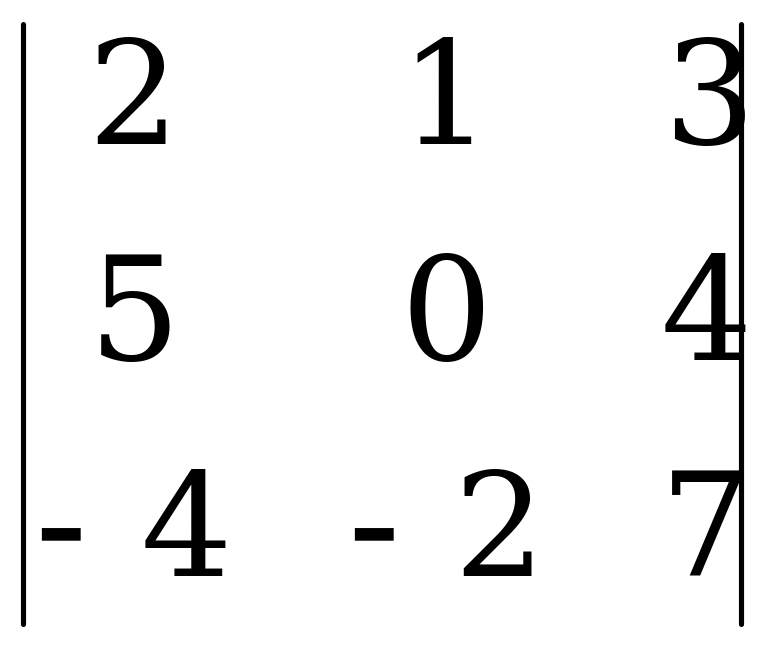 .
.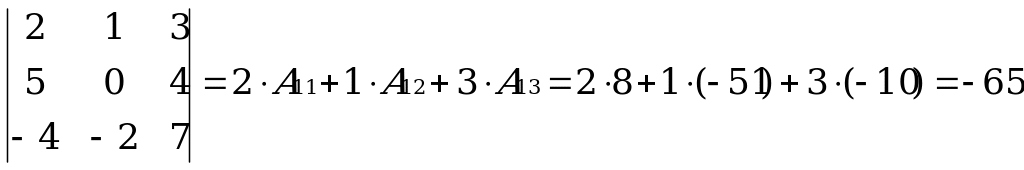 .
.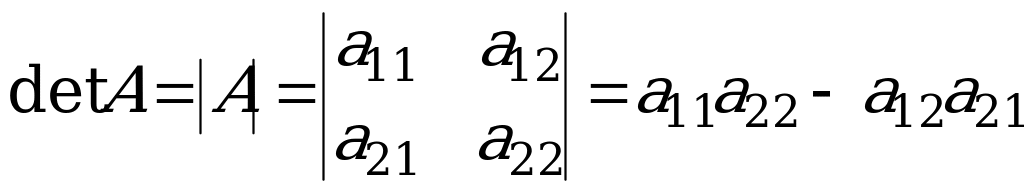
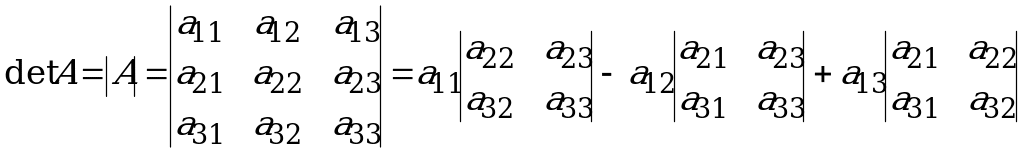
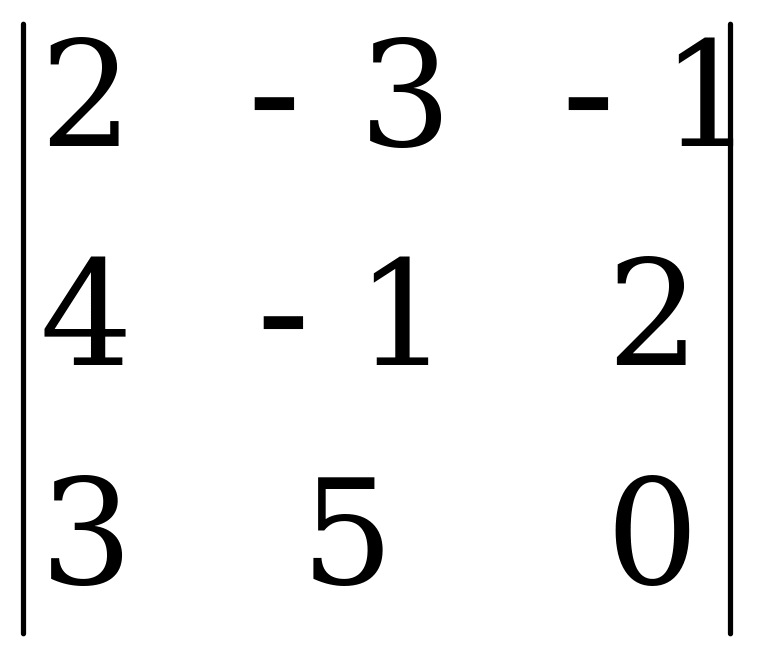
 б)
б)  в)
в)  г)
г) 
 е)
е) 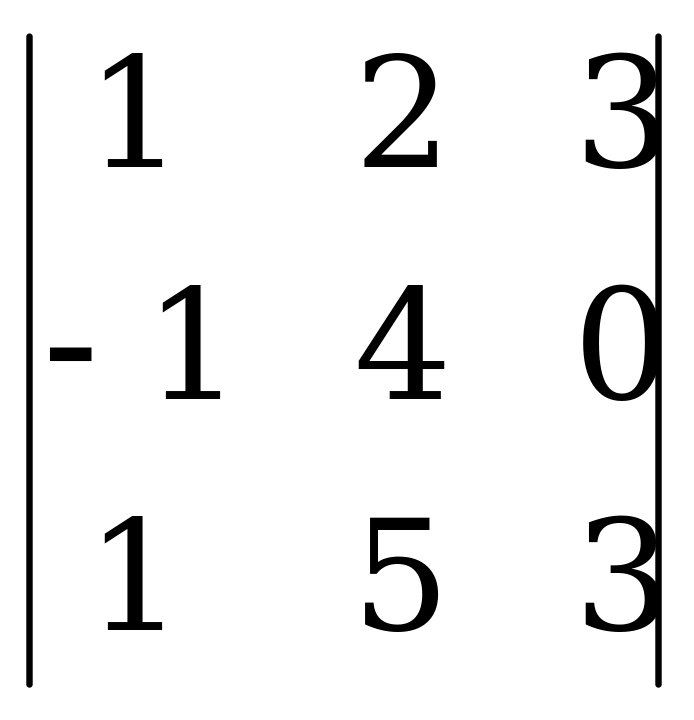 ж)
ж) 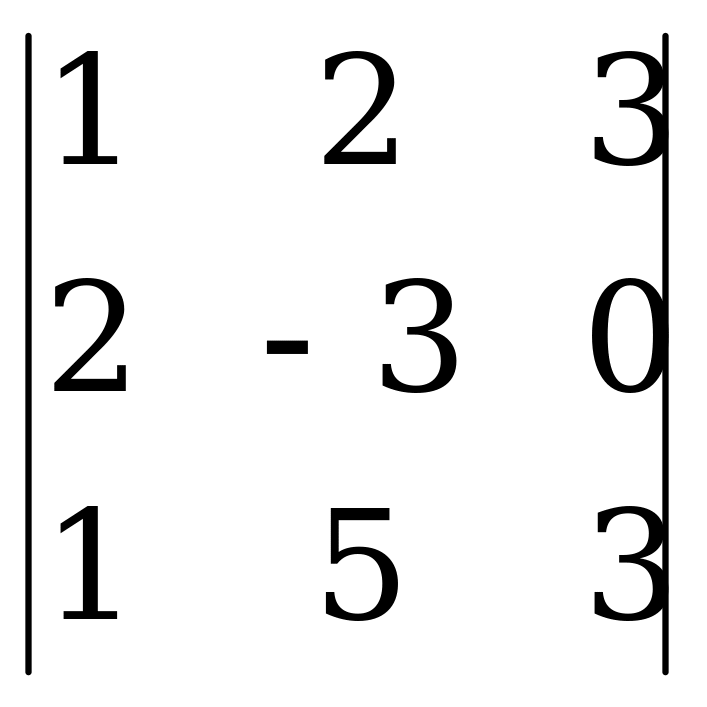 з)
з)