Практическая работа 7
Тема: Вычисление площади поверхности, объема и диагонали параллелепипеда
Цель: Обобщить и систематизировать знания учащихся по теме: «Вычисление площади поверхности, объёма и диагонали параллелепипеда
Ход работы
1. Проверка готовности к практической работе: устный опрос.
2. Выполнение заданий.
1) Для того чтобы выполнить практическую работу, необходимо выбрать соответствующие задания по вашему варианту.
2) Опираясь на теоретический материал, тренировочные упражнения на уроке и домашнее задание, произвести расчет заданий
Справочные материалы.
Параллелепипед — призма, основанием которой является параллелограмм.
Прямой параллелепипед — это параллелепипед, у которого 4 боковые грани — прямоугольники.
Куб — правильный многогранник, каждая грань которого представляет собой квадрат. Частный случай параллелепипеда и призмы.
Прямоугольный параллелепипед — Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники
 Объём прямоугольного параллелепипеда.
Объём прямоугольного параллелепипеда.
Теорема: Объём прямоугольного параллелепипеда с измерениями a, b, c равен произведению всех трех измерений.
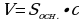
где 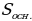 – площадь основания прямоугольного параллелепипеда, c – высота
– площадь основания прямоугольного параллелепипеда, c – высота
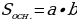
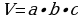
где a – ширина; b – длина; c – высота
Объем любого параллелепипеда равен произведению площади основания на высоту.
V=S(основ.)*h
Площадь боковой поверхности
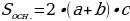
Свойства объемов
-
Объем тела есть неотрицательное число.
2. Равные геометрические тела имеют равные объемы.
3. Если геометрическое тело составлено из геометрических тел, не имеющих общих внутренних точек, то объем данного тела равен сумме объемов тел его составляющих.
Свойства:
-
В прямоугольном параллелепипеде все шесть граней – прямоугольники;
-
Все двугранные углы прямоугольного параллелепипеда – прямые.
Двугранный угол – фигура, образованная прямой а и двумя полуплоскостями с общей границей а, не принадлежащей одной плоскости.
Основные элементы:
-
Грани – прямоугольники, из которых состоит прямоугольный параллелепипед (6 шт.) 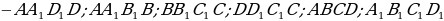

-
Вершины – вершины прямоугольного параллелепипеда (8 шт.) – 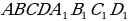
-
Измерения прямоугольного параллелепипеда – длины трех ребер, имеющих общую вершину.
a – ширина
b – длина
c – высота
-
Диагональ – отрезок, соединяющий противоположные вершины
Теорема: Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех измерений
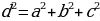
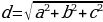
Выразим все три измерения через диагональ:
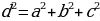
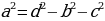
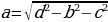
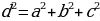
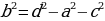
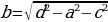
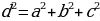
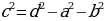
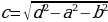
Площадь поверхности прямоугольного параллелепипеда:
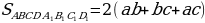
где a – ширина; b – длина; c – высота.
Выразим все три измерения через объём:
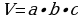
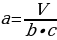
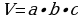
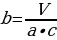
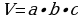
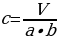
Образец выполнения упражнений:
-
Найдите высоту прямоугольного параллелепипеда, если объем равен 324 мм3, а длина равна 9 мм и ширина – 4 мм.
| Дано: | Решение: | 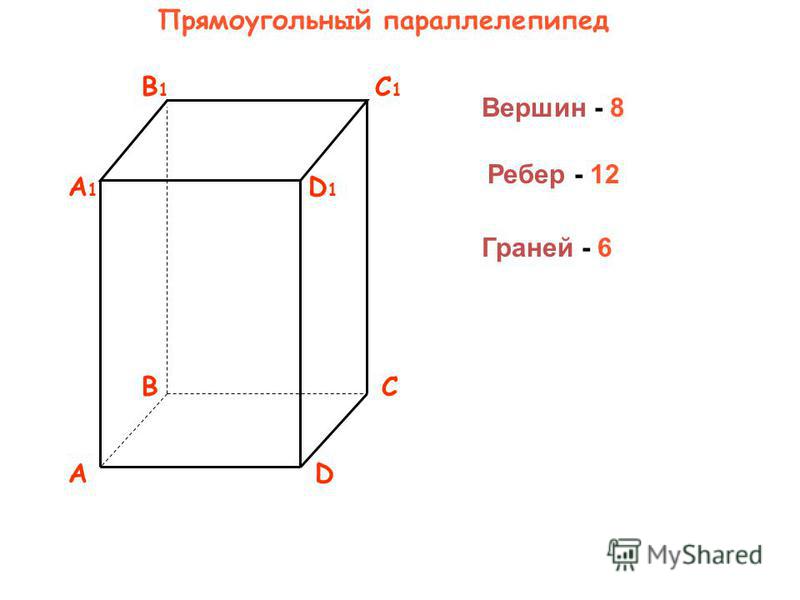
4 9 324 мм3 |
| 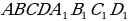 – прямоугольный параллелепипед – прямоугольный параллелепипед
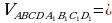 324 мм3 324 мм3
a = 4 мм b = 9 мм | 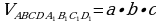 ; ;
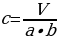
? ; 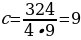 мм мм |
| c - ? |
|
| Ответ: c = 9 мм |
|
|
-
В прямоугольном параллелепипеде диагональ боковой поверхности 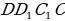 равна 25 см, а высота
равна 25 см, а высота 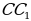 равна 20 см. Найдите длину ребра СВ прямоугольного параллелепипеда, если объем прямоугольного параллелепипеда равен 750 см3 .
равна 20 см. Найдите длину ребра СВ прямоугольного параллелепипеда, если объем прямоугольного параллелепипеда равен 750 см3 .
| Дано: | Решение: | 
? 25 750 см3 20 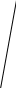 |
| 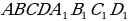 – прямоугольный параллелепипед – прямоугольный параллелепипед
V = 750 см3 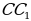 = 20 см = 20 см
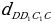 = 25 см = 25 см
СВ - ? | Рассмотрим ∆ 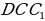 – прямоугольный. – прямоугольный. По теореме Пифагора: DC12 = DC2 + CC12 DC2 = 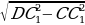 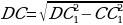
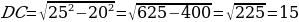 см см
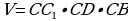
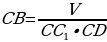
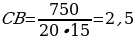 см см
|
| Ответ: 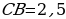 см см |
|
Задачи для практической работы:
| Вариант 1 | Вариант 2 |
| Задача 1. Объем прямоугольного параллелепипеда равен 160 см3. Два его измерения равны 8 см и 10 см. Чему равно третье измерение? | Задача 1. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 24 и 6. Диагональ параллелепипеда равна 39. Найдите объем параллелепипеда. |
| Задача 2. Найдите ширину прямоугольного параллелепипеда, если объём равен 320 см3, а длина равна 8 см и высота – 9 см. | Задача 2. Найдите диагональ прямоугольного параллелепипеда, если измерения равны 8 мм, 11 мм, 13 мм. |
| Задача 3. Длина, ширина и высота прямоугольного параллелепипеда равны соответственно: 18 см, 9 см и 24 см. Вычислить площадь его полной поверхности и сумму площадей оснований. | Задача 3. Длина, ширина и высота прямоугольного параллелепипеда равны соответственно: 15 см, 5 см и 23 см. Вычислить площадь его полной поверхности и площадь боковой поверхности. |
Задание! Решить задачи. Оформление по шаблону:
| Дано:
| Чертеж: | Решение: |
| Ответ: |
Критерии
| Процент результативности (правильных ответов) | Оценка уровня подготовки |
| балл (отметка) | вербальный аналог |
| 90 ÷ 100 | 5 | отлично |
| 80 ÷ 89 | 4 | хорошо |
| 60 ÷ 79 | 3 | удовлетворительно |
| менее 60 | 2 | неудовлетворительно |
2







 Объём прямоугольного параллелепипеда.
Объём прямоугольного параллелепипеда.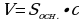
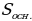 – площадь основания прямоугольного параллелепипеда, c – высота
– площадь основания прямоугольного параллелепипеда, c – высота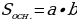
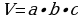
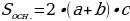
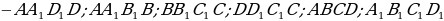

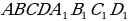
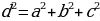
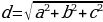
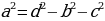
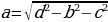
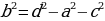
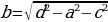
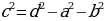
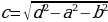
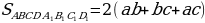
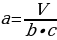
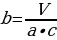
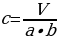

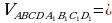 324 мм3
324 мм3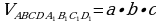 ;
; 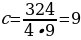 мм
мм 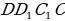 равна 25 см, а высота
равна 25 см, а высота 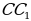 равна 20 см. Найдите длину ребра СВ прямоугольного параллелепипеда, если объем прямоугольного параллелепипеда равен 750 см3 .
равна 20 см. Найдите длину ребра СВ прямоугольного параллелепипеда, если объем прямоугольного параллелепипеда равен 750 см3 .
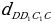 = 25 см
= 25 см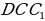 – прямоугольный.
– прямоугольный.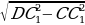
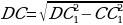
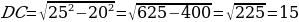 см
см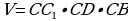
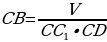
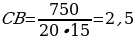 см
см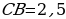 см
см



















