СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Практическое занятие №19 Тема: «Геометрический и физический смысл производной» (комплект КОС УЧЕБНОЙ ДИСЦИПЛИНЫ ОД.03МАТЕМАТИКА ДЛЯ СПЕЦИАЛЬНОСТИ СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ 09.02.06СЕТЕВОЕ И СИСТЕМНОЕ АДМИНИСТРИРОВАНИЕ)
Категория:
Математика
06.12.2024 18:23





 еометрический смысл производной. Если кривая задана уравнением
еометрический смысл производной. Если кривая задана уравнением 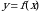 ,
, 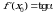 — угловой коэффициент касательной к графику функции в этой точке (
— угловой коэффициент касательной к графику функции в этой точке (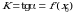 ).
). 

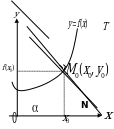
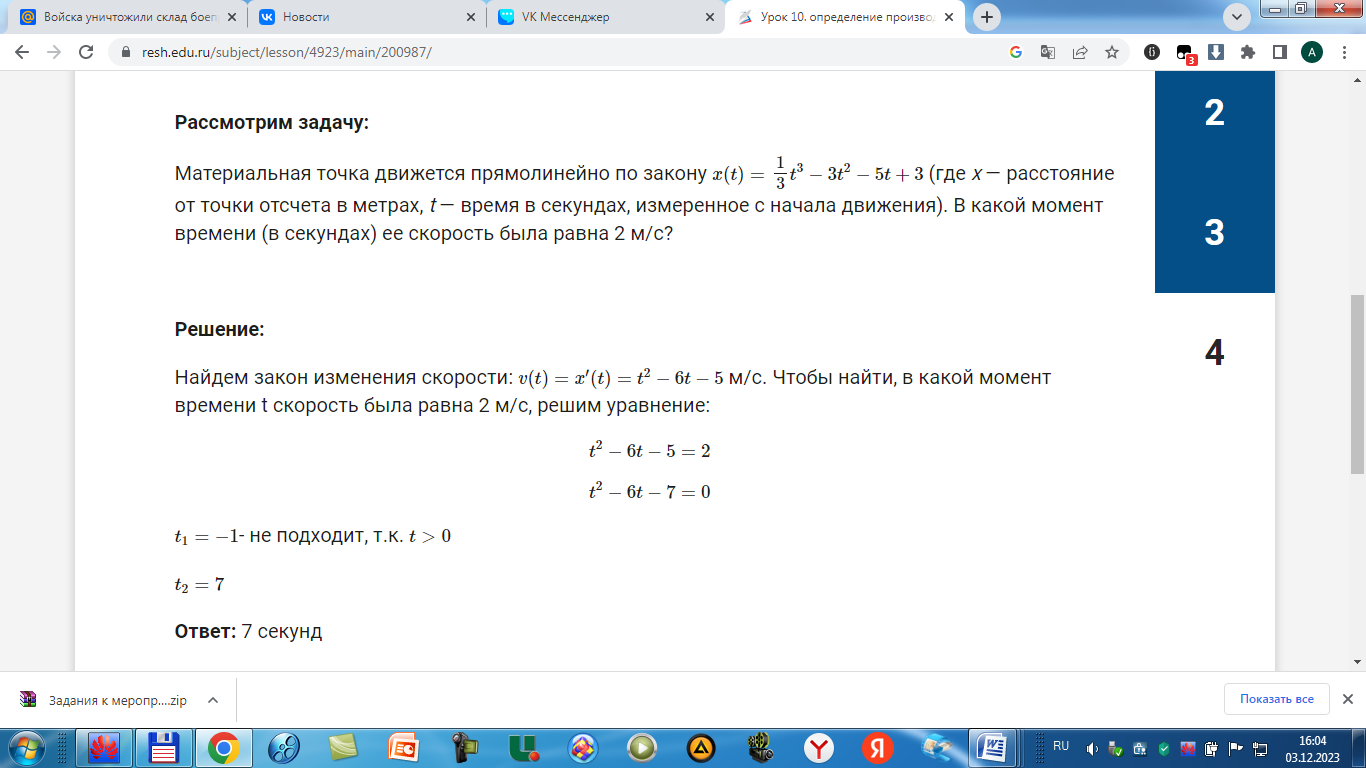 Решение:
Решение: