Практическая работа №4.
Обратная матрица.
Цель занятия:
Учить работать с минорами матрицы;
Учить находить алгебраические дополнения данного определителя;
учить находить обратную матрицу.
Пояснение к работе.
Алгоритм вычисления обратной матрицы:
1. Найти определитель исходной матрицы. Если 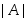 = 0, то матрица А – вырожденная и обратная ей матрица
= 0, то матрица А – вырожденная и обратная ей матрица 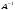 не существует. Если
не существует. Если 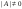 , то матрица А – невырожденная и обратная матрица существует.
, то матрица А – невырожденная и обратная матрица существует.
2. Найти матрицу 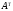 , транспонированную к матрице А.
, транспонированную к матрице А.
3. Найти алгебраические дополнения элементов транспонированной матрицы
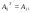 ,
, 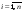 ,
, 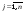 и составить из них присоединенную матрицу
и составить из них присоединенную матрицу
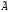 :
: 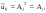 ,
, 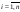 ,
, 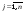 .
.
4. Вычислить обратную матрицу по формуле:
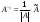 .
.
5. Проверить правильность вычисления обратной матрицы 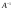 , исходя из ее определения:
, исходя из ее определения: 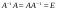 .
.
Вычисление обратной матрицы методом Гаусса:
1) к матрице А приписать справа единичную матрицу Е той же размерности;
2) путем преобразований методом Гаусса над строками расширенной матрицы (А | E) матрица А приводится к единичной матрице;
3) в результате вычислительного процесса на месте приписанной справа матрицы Е получится обратная матрица 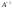 .
.
Схематично процесс нахождения обратной матрицы выглядит следующим образом: (А | E)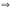 (E |
(E |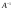 ).
).
Пример . Найти обратную матрицу методом Гаусса для 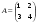 .
.
Решение:
1.Составим расширенную матрицу 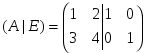 .
.
2. Элементы первой строки умножим на (- 3) прибавим соответственно к элементам второй строки, получим 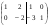 . Затем элементы второй строки прибавим соответственно к элементам первой строки, получим
. Затем элементы второй строки прибавим соответственно к элементам первой строки, получим 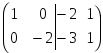 . При выполнении следующего преобразования элементы второй строки умножим на (-1/2). В результате получим матрицу
. При выполнении следующего преобразования элементы второй строки умножим на (-1/2). В результате получим матрицу 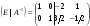 .
.
3. Итак, обратная матрица имеет вид 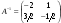 .
.
Варианты заданий
Найдите матрицу, обратную данной матрице.
Проверьте результат, вычислив произведение взаимно обратных матриц, то есть 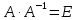
1.  ; 2.
; 2.  ; 3.
; 3.  ; 4.
; 4.  ;
;
5.  ; 6.
; 6.  ; 7.
; 7.  ; 8.
; 8.  ;
;
9.  ; 10.
; 10.  ; 11.
; 11.  ; 12.
; 12.  ;
;
13.  ; 14.
; 14.  ; 15.
; 15.  ; 16.
; 16.  ;
;
17.  ; 18.
; 18.  ; 19.
; 19.  ; 20.
; 20.  ;
;
21. ; 22. ; 23.  ; 24.
; 24. 
25.  ; 26.
; 26.  ; 28.
; 28.  ; 29.
; 29.  .
.







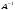 не существует. Если
не существует. Если 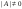 , то матрица А – невырожденная и обратная матрица существует.
, то матрица А – невырожденная и обратная матрица существует.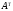 , транспонированную к матрице А.
, транспонированную к матрице А.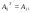 ,
, 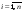 ,
, 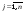 и составить из них присоединенную матрицу
и составить из них присоединенную матрицу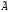 :
: 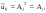 ,
, 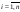 ,
, 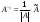 .
.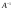 , исходя из ее определения:
, исходя из ее определения: 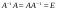 .
.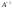 .
.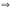 (E |
(E |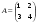 .
.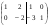 . Затем элементы второй строки прибавим соответственно к элементам первой строки, получим
. Затем элементы второй строки прибавим соответственно к элементам первой строки, получим 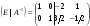 .
.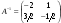 .
.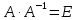
 ; 2.
; 2. 


















