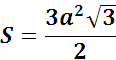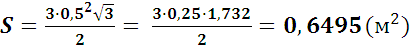Специально к майским праздникам! Скидки до 50% на комплекты видеоуроков и электронных тетрадей

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ

Благодаря готовым учебным материалам для работы в классе и дистанционно

Выбрать материалы

Скидки до 50 % на комплекты
только до 15.05.2025

Готовые ключевые этапы урока всегда будут у вас под рукой

Организационный момент

Проверка знаний

Объяснение материала

Закрепление изученного

Итоги урока

Была в сети 07.05.2025 10:23

Карачева Валентина Ивановна

преподаватель математики

2 180

27 580

Подписчики

Подписки

Местоположение

Россия, Москва

Специализация

Математика

Обо мне Блог Файлы Тесты Галерея Активность Награды

Практическая работа "Площадь поверхности призмы"

Категория: Математика

03.09.2015 21:58

Цели:

закрепить понятия призма, параллелепипед, прямоугольный параллелепипед, линейные размеры, диагональ, площадь боковой и полной поверхности призмы; формировать умения в нахождении призмы среди других пространственных фигур, ее элементов; продолжить формирование умений в применении формул для нахождения площади боковой и полной поверхности призмы в решении практических задач; продолжить формирование интереса к предметным знаниям и приложению знаний в решении практических задач;

Методические указания

Изучить теоретические знания о призме, используя лекционный материал и материал, предложенный в работе. Ответить на контрольные вопросы. Изучить ход практической работы, ответить на контрольные вопросы. Выполнить самостоятельную работу предложенного варианта с оформлением по образцу.

Показать полностью

Просмотр содержимого документа
«Практическая работа "Площадь поверхности призмы"»

Раздел 3 Геометрия

Тема 3.2. Многогранники

Практическая работа №2 «Нахождение элементов призмы, площади ее поверхности»

Виды самостоятельной работы студента: по данным условия задачи найти площадь боковой, полной поверхности призмы

Цели:

закрепить понятия призма, параллелепипед, прямоугольный параллелепипед, линейные размеры, диагональ, площадь боковой и полной поверхности призмы;
формировать умения в нахождении призмы среди других пространственных фигур, ее элементов;
продолжить формирование умений в применении формул для нахождения площади боковой и полной поверхности призмы в решении практических задач;
продолжить формирование интереса к предметным знаниям и приложению знаний в решении практических задач;

Методические указания

Изучить теоретические знания о призме, используя лекционный материал и материал, предложенный в работе.
Ответить на контрольные вопросы.
Изучить ход практической работы, ответить на контрольные вопросы.
Выполнить самостоятельную работу предложенного варианта с оформлением по образцу.

Теоретические знания

Призма — многогранник, две грани которого являются многоугольниками, лежащими в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками.

Виды призм.

Призма, основанием которой является параллелограмм, называется параллелепипедом.

Прямоугольный параллелепипед-это параллелепипед, все грани которого прямоугольники

Прямой параллелепипед-это параллелепипед, у которого 4 боковые грани прямоугольники

Куб-это прямоугольный параллелепипед, все грани которого квадраты.

Прямая призма - это призма, у которой боковые ребра перпендикулярны плоскости основания.

Другие призмы называются наклонными.

Правильная призма - это прямая призма, основанием которой является правильный многоугольник. Боковые грани правильной призмы - равные прямоугольники.

В основании призмы может быть многогранник с любым количеством сторон. От количества сторон зависит название призмы.

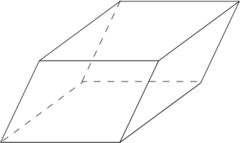
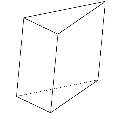
Свойства призмы:

Основания призмы являются равными многоугольниками.
Боковые грани призмы являются параллелограммами.
Боковые ребра призмы параллельны и равны.

Площадь боковой поверхности прямой призмы

S_б.п. = P•H

где P — периметр основания призмы (сумма всех сторон основания), H — высота призмы. Высота прямой призмы совпадает с боковым ребром.

Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания

S_п.п. = P•H +2• S_осн

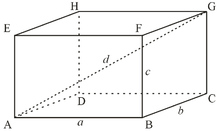
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его линейных размеров: d² = a²+b² +c²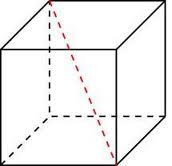

Контрольные вопросы

Среди изображенных тел, выберите те, которые

являются многогранниками. Какие из них являются призмами ?

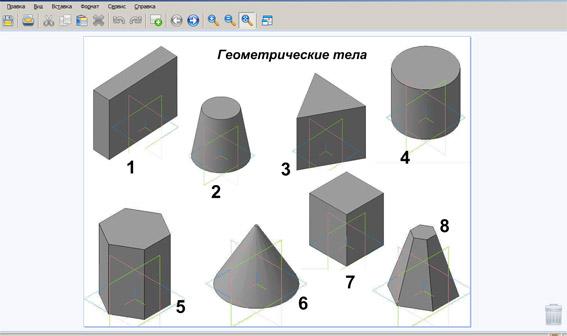
Покажите для призмы :

а) вершины б) основания в) грани г) ребра

Какие многогранники лежат в основании призмы? В каких плоскостях лежат основания призм?
Какими отрезками являются боковые ребра призмы?
Какими многоугольниками являются все грани параллелепипеда?
Сколько измерений у прямоугольного параллелепипеда?
Какие многоугольники являются основаниями и боковой гранью прямоугольной призмы (четырехугольной, пятиугольной)?Сколько граней у треугольной (четырехугольной, пятиугольной ) призмы ?
Из каких поверхностей состоит площадь боковой поверхности призмы, площадь полной поверхности призмы?
Запишите формулу для нахождения площади боковой и полной поверхности прямоугольного параллелепипеда.
Запищите формулу для нахождения диагонали прямоугольного паралелепипеда.

Задание к практической работе: по данным моделям найти площадь боковой, полной поверхности призмы

Пример: Найти площадь боковой, полной поверхности призмы.

Ход работы

1.Для нахождения площади боковой поверхности призмы нужно измерить линейкой следующие элементы призмы: стороны основания, высоту. Подставить значения в формулу для нахождения площади (если призма прямая)

2. Для нахождения площади полной поверхности призмы нужно найти площадь основания призмы (площадь треугольника, прямоугольника, ромба)

Площадь полной поверхности призмы находится как сумма площадей боковой поверхности и двух оснований.

Оформление работы:

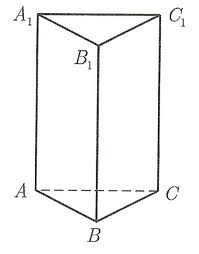
Дано: АВСС₁В₁А₁ треугольная призма, прямая, правильная

АВ=ВС=АС = 5 см, Н = 10 см

Найти: S_б.п., S_п.п.

Решение: S_б.п. = P•H

Р=5+5+5=15(см), Н=10см

S_б.п.= 15•10 = 150 (см²)

Фо́рмула Герона позволяет вычислить площадь треугольника (S) по его сторонам a, b, c:

S_осн= √р(р-а)(р-в)(р-с)

где p — полупериметр треугольника: р = (а+в+с):2

р= 15:2 =7,5(см) S_п.п. = P•H +2• S_осн,= 150 + 2•7,7 = 164,4 (см²)

Решение задачи практического характера

Коллекционер заказал аквариум, имеющий форму правильной шестиугольной призмы. Сколько квадратных метров стекла необходимо для изготовления аквариума, если сторона основания 0,5 м, а высота 1,2 м? Ответ округлите до сотых.

Сначала найдём площадь основания.

Так как основание – правильный шестиугольник, то площадь основания найдём по формуле: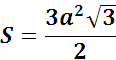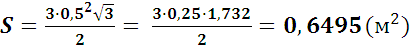

2. Найдём площадь боковой поверхности:

0,5∙1,2∙6= 3,6(м²)

3.Площадь полной поверхности найдём по формуле:

S=Sбок+Sосн=3,6+2∙0,6495=4,899(м²₎

Ответ: 4,90 м²

Контрольные вопросы

Какие измерения нужны для вычисления площади боковой и полной поверхности призмы?
Как вычислить периметр основания призмы?
Запишите формулы для вычисления площади боковой и полной поверхности призмы?
Какие изменения произойдут при вычислении площади боковой и полной поверхности правильной четырехугольной, пятиугольной, шестиугольной призмы.

Задания для самостоятельной работы:

Вариант 1

1. Сколько ребер у шестиугольной призмы?

Ответ: а)18, б)24, в)12.

2.Выберите верное утверждение.

а) призма называется правильной, если ее основания - правильные многоугольники;

б) у треугольной призмы две диагонали;

в) высота призмы равна ее боковому ребру;

3.Задача Найдите площадь боковой и полной поверхности прямоугольного параллелепипеда, если его измерения равны 2м, 3м, 5м.

4. Задача. Коллекционер заказал аквариум, имеющий форму правильной четырехугольной призмы. Сколько квадратных метров стекла необходимо для изготовления аквариума, если сторона основания 70 см, а высота 60 см?

Вариант 2

1.Сколько граней у шестиугольной призмы?

Ответ: а)6, б)8, в)10

2. Выберите верное утверждение.

а) площадь полной поверхности призмы называется сумма площадей ее боковых граней и основания;

б) у треугольной призмы нет диагоналей;

в) высота прямой призмы равна ее боковому ребру;

3.Задача. Найдите площадь боковой и полной поверхности прямоугольного параллелепипеда, если его измерения равны 3см, 4см, 5см.

4. Задача Необходимо изготовить короб с крышкой для хранения картофеля в форме прямой призмы высотой 0,7 м. В основании призмы лежит прямоугольник со сторонами 0,4 м и 0,6 м. Сколько фанеры понадобится для изготовления короба?

Вариант 3(задания повышенного уровня)

1.Сколько граней у четырехугольной призмы?

Ответ: а)6, б)8, в)10

2. Выберите верное утверждение.

а) У n – угольной призмы 2 n ребер;

б) площадь полной поверхности призмы называется сумма площадей ее боковых граней;

в) у треугольной призмы три диагонали;

3.Задача. Сколько необходимо купить листов 8 – волнового шифера размером 1750*1130 мм на покрытие крыши здания длиной 10 м. Фронтон имеет форму равнобедренного прямоугольного треугольника с гипотенузой 10 м и катетом 7 м.

4. Задача. Нужно оклеить обоими типа «рогожка», комнату, длина которой 6м, ширина 4м, высота 3м, площадь окон и дверей составляет 1/5 всей площади стен. Сколько нужно рулонов обоев для оклейки комнаты, если длина рулона 12 м, а ширина 50 см?

Формы контроля

Своевременное выполнение. Оформление работы. Правильное использование формул для вычисления, отсутствие вычислительных ошибок.

Литература

Башмаков М.И. Математика. Учебное пособие для общеобразовательных учреждений нач. и сред. проф. образования

Интернет-ресурсы

http://fcior.edu.ru/- «Федеральный центр информационно-образовательных ресурсов». Модули: Правильные многогранники. Призма. Параллелепипед.
ru.wikipedia.org› Правильный многогранник. Призма. Параллелепипед.