МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД
ГБПОУ РД «КАСПИЙСКОЕ МЕДИЦИНСКОЕ УЧИЛИЩЕ им. А. Алиева»

Информатика
Практикум для первых курсов
Семетр)
Каспийск 2022
Авторы:
Латифов Абдулатиф Саидович Кандидат Педагогических. Наук. преподаватель информатики и ИКТ ГБПОУ РД «Каспийское медицинское училище им А. Алиева»
Умарова Шахризат Нурмагомедовна преподаватель информатики ГБПОУ РД «Каспийское медицинское училище им А. Алиева»
Книга предназначен для студентов СПО. Содержит практический материал соответствии, государственным программам рекомендуемый ФГОС РФ, для первых курсов, закрепления практических навыков и является учебным пособием для подготовки к итоговой аттестации.
Рецензент: д.п. н. профессор, зав кафедры ИКТ ФГБОУ ВО ДГПУ Сурхаев М.А.
Практическое занятие №1
Единицы измерения информации
Информацию принято мерить битами и байтами. Самое маленькое значение это 1 бит меньше нет, но однако при измерении информации на носителях обычно не берут единицу ниже байта.
Байт — это набор из 8 битов.
1 байт = 8 бит
Если информации становиться больше мы прибегаем к более крупным единицам килобайтам.
1 килобайт = 1024 байт
Если и килобайтов становиться больше, то мы уже будем иметь дело с мегабайтом.
1 мегабайт = 1024 килобайт
1 гигабайт = 1024 мегабайт
1 терабайт = 1024 гигабайт
1 петабайт = 1024 терабайт
1 эксабайт = 1024 петабайт
1 зеттабайт = 1024 эксабайт
Теперь давайте поговорим как переводить единицы измерения из одной в другую и когда это может понадобиться.
Например, у вас такая задача. Вам известно, что ваш файл весит 700 000 килобайт, а флешка имеет объем 2 гигабайта. И вам нужно понять поместиться ваш файл на флешку или нет.
Просто сверить эти два значения не представляется возможным потому что они даны в разных единицах измерения килобайт и гигабайт. Нам нужно перевести одну из них в одинаковую единицу. Переведем килобайты в гигабайты.
Для этого введем такое правило.
Если вы переводите единицы измерения из меньшего в большую, то вы будете делить.
Если вы переводите из более крупной в меньшую, то вы умножаете.
В данном нашем случае мы переводим килобайты в гигабайты. Значит нам нужно подняться на 2 ступени по весу единицы измерения. Вес становиться больше поэтому мы делим дважды на значение 1024. Так как это значение связывает наши единицы измерения.
700 000 килобайт: 1024 = 683,6 мегабайт
Поделив один раз на 1024, мы попадем в мегабайты.
683,6 мегабайт: 1024 = 0,7 гигабайт
Мы перешли из мегабайтов в гигабайты. Теперь можем легко сравнивать 0,7 гигабайт . Наш файл поместиться на флешку.
Решим еще несколько примеров.
Переведем 85 мегабайт в байты.
Что бы перевести мегабайты в байты нужно определить направление нашего движения. Мы идем от более крупных к мелким или наоборот. Конечно видно, что мегабайты более крупные единицы. Значит мы в нашей табличке движемся вверх, будем умножать. Нам нужно сделать 2 действия пройти от мегабайта к килобайтам, а затем к байтам.
85 мегабайт * 1024 = 87 040 килобайт
87 040 килобайт * 1024 = 89 128 960 байт
0,5 петабайт в гигабайты.
0,5 петабайт * 1024 = 512 терабайт
512 терабайт * 1024 = 524 288 гигабайт
100 килобайт в байты
100 килобайт * 1024 = 102 400 байт
102 400 байт * 8 = 819 200 бит
342000 бит в мегабайты
342 000 бит / 8 = 42 750 байт
42 750 байт / 1024 = 41,7 килобайтов
41,7 килобайта / 1024 = 0,04 мегабайта
Итак, что вам нужно запомнить при переводе из одной единицы в другую. Если единица измерения повышается при переводе вам нужно делить. Если единица измерения уменьшается, то вам нужно умножать. применяется обратно пропорциональная связь.
Единица измерения количества информации называется бит (bit – binary digit), что означает двоичный разряд.
Количество информации – это количество бит в сообщении.
Сообщение, уменьшающее информационную неопределенность (неопределенность знаний) в два раза, несет для него 1 бит информации.
Пример_1: Книга лежит на одной из двух полок – верхней или нижней. Сообщение о том, что книга лежит на верхней полке, уменьшает неопределенность ровно вдвое и несет 1 бит информации.
Сообщение о том, что произошло одно событие из двух равновероятных, несет 1 бит информации.
Научный подход к оценке сообщений был предложен еще в 1928 году Р. Хартли.
Пусть в некотором сообщении содержатся сведения о том, что произошло одно из N равновероятных событий (равновероятность обозначает, что ни одно событие не имеет преимуществ перед другими). Тогда количество информации, заключенное в этом сообщении, - x бит и число N связаны формулой:
2x = N
где x – количество информации или информативность события (в битах);
N – число равновероятных событий (число возможных выборов).
Данная формула является показательным уравнением относительно неизвестной x. Решая уравнение, получим формулу определения количества информации, содержащемся в сообщении о том, что произошло одно из N равновероятных событий, которая имеет вид:
x = log2N
логарифм от N по основанию 2.
Если N равно целой степени двойки, то такое уравнение решается легко, иначе справиться с решением поможет таблица логарифмов.
Если N = 2 (выбор из двух возможностей), то x = 1 бит.
Пример_2: Какое количество информации несет сообщение о том, что встреча назначена на июль?
Решение: В году 12 месяцев, следовательно, число равновероятных событий или число возможных выборов N = 12. Тогда количество информации x = log212. Чтобы решить это уравнение воспользуемся таблицей логарифмов или калькулятором.
Ответ: x = 3,58496 бита.
Задание 1. Измерьте информационный объем сообщения «Ура! Скоро Новый год!» в битах, байтах, килобайтах (Кб), мегабайтах (Мб).
Указание: считается, что текст набран с помощью компьютера, один символ алфавита несет 1 байт информации. Пробел – это тоже символ в алфавите мощностью 256 символов.
Задание 2. Измерьте примерную информационную емкость одной страницы любого своего учебника, всего учебника.
Указание: Для выполнения задания возьмите учебник по любимому предмету, посчитайте число строк на странице, число символов в строке, включая пробелы. Помните, что один символ алфавита несет 1 байт информации. Перемножив полученные значения, Вы найдете информационную емкость одной страницы учебника (в байтах).
Задание 3. Информационное сообщение объемом 1.5 Кбайта содержит 3072 символа. Сколько символов содержит алфавит, при помощи которого было записано это сообщение? (Объяснение решения задачи на доске).
Задание 4. Подсчитать в килобайтах количество информации в тексте, если текст состоит из 600 символов, а мощность используемого алфавита – 128 символов.
Задание 5. Скорость информационного потока – 20 бит/сек. Сколько времени потребуется для передачи информации объемом в 10 килобайт.
Задание 6. Сравните (поставьте знак отношения)
200 байт и 0,25 Кбайт.
3 байта и 24 бита.
1536 бит и 1,5 Кбайта.
1000 бит и 1 Кбайт.
8192 байта и 1 Кбайт.
Задание 7. Книга, набранная с помощью компьютера, содержит 150 страниц; на каждой странице — 40 строк, в каждой строке — 60 символов. Каков объем информации в книге?
Задание 8. Подсчитайте объем информации, содержащейся в романе А. Дюма "Три мушкетера", и определите, сколько близких по объему произведений можно разместить на одном лазерном диске? (590 стр., 48 строк на одной странице, 53 символа в строке).
Задание 9. Какое количество информации несет сообщение: “Встреча назначена на сентябрь”.
Задание 10. Сообщение занимает 3 страницы по 25 строк. В каждой строке записано по 60 символов. Сколько символов в использованном алфавите, если все сообщение содержит 1125 байтов?
Задание 11. Измерьте информационный объем сообщения “Ура! Закончились каникулы!!” (с точки зрения технического подхода, то есть не учитывая смысл сообщения). Выразите этот объем в битах, байтах, килобайтах.
Задание 12. Считая, что каждый символ кодируется одним байтом, оцените информационный объём следующего предложения в кодировке КОИ-8 (в байтах):
Сегодня метеорологи предсказывали дождь.
Практические занятия №2 и №3
Система счисления. Двоичное представления информации.
Модель перевода чисел из одной системы счисления в другую
В двоичной системе счисления все числа записываются с помощью двух цифр 0 или 1, основание (базис) двоичной системы счисления q=2.
В восьмеричной системе счисления все числа записываются с помощью восьми цифр 0, 1, 2, 3, 4, 5, 6, 7, основание восьмеричной системы счисления q=8.
В десятичной системе счисления все числа записываются с помощью десяти цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
В шестнадцатеричной системе счисления все числа записываются с помощью шестнадцати цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A (количественный эквивалент числа 10), B (11), C (12), D(13), E (14), F (15), базис шестнадцатеричной системы счисления q=16. Рассмотрим соотношение цифр и чисел в различных системах счисления (Таблица 1).
Таблицы чисел в различных системах счисления Таблица 1
| 10-я | 2-я | 8-я | 16-я |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
| 16 | 10000 | 20 | 10 |
| Для того чтобы перевести целую часть числа из десятичной системы счисления в двоичную, восьмеричную, шестнадцатеричную, необходимо: 1. Последовательно делить данное число и получаемые при делении целые частные на основание q новой системы счисления (2, 8 или 16), выражая промежуточный результат цифрами исходной системы, до тех пор, пока частное не станет равным нулю. 2. Полученные остатки, фактически являющиеся цифровым выражением числа в новой системе, привести в соответствие с алфавитом этой системы счисления (имеются в виду системы счисления с основанием больше 10). 3. Записать число в новой системе счисления, начиная с последнего остатка. | Пример 1. Перевести число 2310 в двоичную систему счисления.
| _23 |
| 2 |
|
|
|
|
|
|
|
| | 22 |
| _11 |
| 2 |
|
|
|
|
|
| |  |
| 10 |
| _5 |
| 2 |
|
|
|
| |
|
| |
| 4 |
| _2 |
| 2 |
|
| |
|
|
|
| |
| 2 |
| _1 |
| 2 | |
|
|
|
|
|
| |
| 0 |
| 0 | |
|
|
|
|
|
|
|
| |
|
| |
|
|
|
|
|
|
|
|
|
|
| Получаем 2310=101112 |
Для того, чтобы выполнить перевод правильных дробей из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную необходимо последовательно умножать правильную дробь и получаемые дробные части произведений на основание системы q до тех пор, пока дробная часть произведения не станет равной нулю или не будет достигнута требуемая точность представления числа.
Полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления. Составить дробную часть числа в новой системе счисления, начиная с целой части первого произведения.
Пример 2. Перевести число 0,6562510 в восьмеричную систему счисления.
| 0, | 65625 х 8 |
| 5, | 25000
х 8 |
| 2, | 00000 |
Получаем: 0,6562510 = 0,528
Перевод вещественных чисел, т.е. чисел, содержащих целую и дробную части, осуществляется в два этапа. Отдельно переводится целая часть, отдельно — дробная. В итоговой записи полученного числа целая часть отделяется от дробной запятой.
| Пример 3. Перевести число 156,35610 в шестнадцатеричную систему счисления. Представим число в виде суммы целой и дробной части 156,35610=15610+0,35610 Переводим целую часть 15610 в шестнадцатеричную систему счисления: | _156 |
| 16 |
|
| | 144 |
| _9 |
| 16 | | 12 |
| 0 |
| 0 | | (С) |
| 9 |
|
| Получаем 15610=9С16 | Переводим дробную часть 0,35610 в шестнадцатеричную систему счисления: | 0, | 356
х 16 | | 5, | 696
х 16 | | 11, (В) | 136
х 16 | | 2, | 176… | Получаем: 0,35610 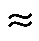 0,5В216. 0,5В216. |
Таким образом, 9С16+0,5В216=9С,5В216. Получаем: 156,35610 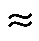 9С,5В216
9С,5В216
При переводе чисел из системы счисления с основанием q в десятичную систему счисления необходимо пронумеровать разряды целой части справа налево, начиная с нулевого, и дробной части, начиная с разряда сразу после запятой, слева направо – начальный номер -1. Затем вычислить сумму произведений соответствующих значений разрядов на основание q системы счисления в степени, равной номеру разряда
Пример 4. Перевести число 10110110111,1012 в десятичную систему счисления
| 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | -1 | -2 | -3 |
| 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1, | 1 | 0 | 12=1*29+0*28+1*27+1*26+0*25+1*24+1*23+0*22+1*21+ |
+1*20+1*2-1+0+2-2+1*2-3= =512+0+128+64+0+16+8+0+2+1+0,5+0+0,125=731,62510
Если необходимо перевести число из двоичной системы счисления в систему счисления, основанием которой является степень двойки, достаточно объединить цифры двоичного числа в группы по столько цифр, каков показатель степени. При этом в целой части числа группировка производится справа налево, а в дробной слева направо. Если в последней группе недостает цифр, дописываются нули: в целой части - слева, в дробной – справа. Затем каждая группа заменяется цифрой новой системы счисления (Таблица 1).
При переводе чисел из системы счисления, основанием которой является степень двойки, в двоичную систему счисления необходимо каждую цифру заменить группой по столько цифр двоичной системы счисления, каков показатель степени. Затем записать цифры слева направо.
Пример 5. Перевести число 1011010010111,10112 в восьмеричную систему счисления
Разбиваем число на тройки цифр и заменяем каждую триаду восьмеричной цифрой:
001 011 010 010 111,101 1002
1 3 2 2 7 5 4
Получим 1011010010111,1011002=13227,548
Пример 6. Перевести число 801А9Е,3F16 в двоичную систему счисления
Заменим каждую цифру четверкой двоичных цифр: 8 0 1 А 9 Е, 3 F16
1000 0000 0001 1010 1001 1110 0011 1111
Получим 801А9Е,3F16=100000000001101010011110,001111112
Задания к практической работе
1) Выполнить перевод целых чисел из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления:
2610 | 2710 | 2810 | 2910 | 3010 | 3110 | 4210 | 4310 | 4410 | 4510 |
4610 | 4710 | 5810 | 5910 | 6010 | 6110 | 6210 | 6310 | 7410 | 7510 |
7610 | 7710 | 7810 | 7910 | 9010 | 9110 | 9210 | 9310 | 9410 | 9510 |
2) Выполнить перевод правильных дробей из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления:
0,2510 | 0,12510 | 0,3410 | 0,3710 | 0,3910 | 0,4110 | 0,4410 | 0,4910 |
3) Выполнить перевод вещественных чисел из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления:
106, 12510 | 107,45610 | 108,37510 | 109,37710 | 110,37810 |
111,37910 | 122,38110 | 123,38210 | 124,38310 | 125,38410 |
126,38510 | 127,38610 | 138,38710 | 139,38810 | 140,38910 |
141,39110 | 142,39310 | 143,39410 | 154,39510 | 155,39610 |
156,39110 | 157,39210 | 158,39310 | 159,39410 | 170,39510 |
171,39610 | 172,39710 | 173,39810 | 174,39910 | |
Практическое занятие 4
Решение задач с использованием количества информации и на перевод единиц измерения
1 байт = 8 битов.
Существуют еще более крупные единицы измерения информации.
Переход к более крупным единицам измерения информации (килобайт, мегабайт, терабайт, петабайт, эксабайт). Байт наиболее удобная единица измерения информационного объема сообщения, состоящего из последовательности символов компьютерного алфавита. Однако она мала при подсчете емкости информационных носителей. По аналогии с физическими единицами измерения (например, 1 килограмм = 1000 грамм) подбираем по таблице целых степеней двойки значение близкое к тысячи.
При алфавитном подходе к определению количества информации отвлекаются от содержания (смысла) информации и рассматривают информационное сообщение как последовательность знаков определенной знаковой системы. Алфавитный подход является объективным, т.е. он не зависит от человека, воспринимающего текст. Если допустить, что все символы встречаются в сообщении с одинаковой частотой (равновероятно), то количество информации, которое несет каждый символ, вычисляется по формуле:
2i = N,
где N – мощность алфавита,
i – информационный вес одного символа
Количество информации, заключенной в тексте, вычисляется по формуле:
I = i ∙ K,
где i – информационный вес одного символа;
K – количество символов в сообщении
I – количество информации
Вероятностный подход
В жизни мы сталкиваемся не только с равновероятными событиями, но и с событиями, которые имеют разную вероятность реализации. Например:
не все буквы алфавита встречаются одинаковое количество раз;
сообщение, что будет дождь более вероятно летом, а о снеге зимой;
если в мешке лежат 10 белых шаров и 3 черных, то вероятность вытащить белый шар больше, чем вероятность вытащить черный.
Вероятность выражается в долях единицы. В частном случае, вероятность достоверного события равна 1, вероятность невозможного события равна 0.
Качественную связь между вероятностью события и количеством информации в сообщении об этом событии можно выразить так: чем меньше вероятность некоторого события, тем больше информации содержит сообщение об этом событии.
Вероятность высчитывается по формуле:
P = K/N,
где P – вероятность события
K – количество раз, которое может произойти данное событие
N – общее число возможных исходов какого-то события
Например, в коробке 50 шаров, из них 40 белых и 10 черных. Какова вероятность того, что достали белый шар? Черный шар?
Pб = 40/50 = 0,8 (вероятность того, достали белый шар)
Pч = 10/50 = 0,2 (вероятность того, достали черный шар)
Количественная зависимость между вероятностью и количеством информации выражается формулой:
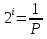
1. В коробке 32 карандаша, все карандаши разного цвета. Наугад вытащили красный. Какое количество информации при этом было получено? При решении задачи используйте формулу Р. Хартли
N = 2I ,
где N – число возможных событий,
I – количество информации в битах.

Ответ: 5
2. В школьной библиотеке 16 стеллажей с книгами, на каждом – по 8 полок. Ученику сообщили, что нужный учебник находится на 2-ой полке 4-го стеллажа. Какое количество информации получил ученик?
Существует 16*8 = 128 вариантов местонахождения книги. Из этих количеств вариантов необходимо выбрать один.
N = 128, а I = 7, т.к. 128 = 2^7
Ответ: 7 бит.
Задача . Первое письмо состоит из 50 символов 32-символьного алфавита, а второе – из 40 символов 64 – символьного алфавита. Сравните объемы информации, содержащиеся в двух письмах.
Дано:
К1 = 50 с.,
К2 = 40 с.,
N1 = 32,
N2 = 64,
I1 - ?
I2 - ?
Решение:
I = K*i, N = 2i,
Определим информационную емкость одного символа в каждом из писем:
2i = 32, i = 5 бит – для первого письма,
2i = 64, i = 6 бит – для второго письма.
Определим количество информации в каждом из писем:
50*5 = 250 бит – для первого письма,
40*6 = 240 бит – для второго письма.
Найдем разность между информационными объемами двух писем.
250 - 240 = 10 бит.
Ответ: Объем информации, содержащейся в первом письме на 10 бит больше, чем объем информации, содержащейся во втором письме.
Задача . Для хранения текста требуется 84000 бит. Сколько страниц займёт этот текст, если на странице размещается 30 строк по 70 символов в строке?
Решение:
1 байт=8 бит. 84000/8=10500 символов в тексте. На странице помещается 30×70=2100 символов. 10500/2100=5 страниц.
Ответ: текст займёт 5 страниц.
Задача . В корзине лежат шары. Все разного цвета. Сообщение о том, что достали синий шар, несёт 5 бит информации. Сколько всего шаров было в корзине?
Решение:
Если все шары разного цвета, значит, ни один шар не совпадает по цвету с другими. Следовательно, шары можно доставать с равной долей вероятности. В этом случае применяется формула Хартли. iсиний = 5 бит; 5 = log232; 2i = N; 25 = 32.
Ответ: в корзине 32 шара.
Задача . Сколько символов содержит сообщение, записанное с помощью 16-символьного алфавита, если его объём составил 1/16 часть мегабайта?
Решение:
1 Мб=1024 Кб. Значит, объём сообщения 1024/16=64 Кб. Информационный вес символа iсимв.=log216= 4 бит. Объём сообщения в битах - 64×1024×8=524 288 бит. Количество символов в сообщении 524288/4=131 072.
Ответ: в сообщении 131 072 символа.
| Сообщение, записанное буквами из 16 символьного алфавита, содержит 10 символов. Какой объем информации в битах оно несет? | | 
| | Дано: Мощность алфавита N = 16
текст состоит из 10 символов Определить объем информации в битах. | Решение: 1. 16 = 2 4, значит вес одного символа b = 4 бита. 2. Всего символов 10, значит объем информации 10 * 4 = 40 бит. Ответ: сообщение несет 40 бит информации (8 байт). |
| Информационное сообщение объемом 300 бит содержит 100 символов. Какова мощность алфавита? | | 
| | Дано: Объем сообщения = 300 бит
текст состоит из 100 символов Какова мощность алфавита? | Решение: 1. Определим вес одного символа: 300 / 100 = 3 бита. 2. Мощность алфавита определяем по формуле: 2 3 = 8. Ответ: мощность алфавита N = 8. |
Практическое занятие №5
Линейные алгоритмы . определение . блок – схема. Виды блок - схем
Линейные алгоритмы
Линейный алгоритм является наиболее простым. В нём предполагается последовательное выполнение операций. В этом алгоритме не предусмотрены проверки условий или повторений.
Пример: Вычислить функцию z= (х-у)/x +y2.
Составить блок-схему вычисления функции по линейному алгоритму. Значения переменных х, у могут быть любые, кроме нуля, вводить их с клавиатуры.
Решение: Линейный алгоритм вычисления функции задан в виде блок-схемы на рис.1. При выполнении линейного алгоритма значения переменных вводятся с клавиатуры, подставляются в заданную функцию, вычисляется результат, а затем выводится результат.
В примере 1 алгоритм задаётся словесно, графически он даётся в виде схемы на рис.1.1 в примере 6, где не требуется описания алгоритма, так как он представляется наглядно.
Пример 6.
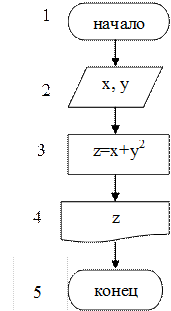
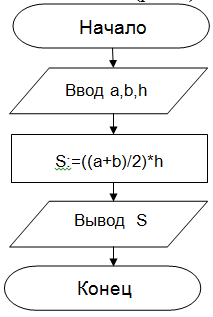
Задание 1. Определить площадь трапеции по введенным значениям оснований (a и b) и высоты (h).
Запись решения задачи на алгоритмическом языке:
алг трапеция
вещ a,b,h,s
нач
ввод f,b,h
s:=((a+b)/2)*h
вывод s
кон
Запись алгоритма в виде блок-схемы (рис. 1):
Задание 2
Коллекция Эрмитажа содержит более 2 800 ООО единиц хранения. Если у каждого музейного экспоната задержаться всего на 5 минут и проводить в Эрмитаже по 8 часов каждый день, то может не хватить жизни, чтобы ознакомиться со всей коллекцией. Требуется вычислить суммарное время просмотра всей коллекции в минутах, часах, днях, годах, «жизнях», считая, что средняя продолжительность жизни в Роcсии составляет 70 лет.
| Словесный алгоритм
Начало алгоритма
1. Введите количество экземпляров коллекции.
2. Рассчитайте время просмотра всех экземпляров:
• в минутах;
• в часах;
• в днях;
• в годах;
• в «жизнях».
3. Выведите результаты расчетов.
Конец алгоритма | 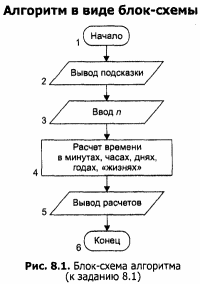
|

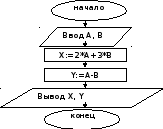
Задание № 1. По блок-схеме определить значения переменных X, Y, при данных значениях А, В.
Практическая работа №6
Разветвляющие алгоритмы. Определение
Ветвление — алгоритм, в котором предусмотрены разветвления, указанные в последовательности действий на два направления в зависимости от итогов проверки заданного условия. То есть такой алгоритм, обязательно содержит условие и в зависимости от результата выполнения условия происходит выбор действия. Например: Если день рабочий, то идем в лицей, иначе будем отдыхать. Таких примеров можем привести много из обычной жизни и наук. К примеру, физика: Если удар упругий, то масса тела сохраняется, иначе масса изменяется. Алгоритмическая конструкция ветвление программируется с помощью условного оператора If, который может быть представлен двумя вариантами (Таблица 1)
Задание 1 Определить среднее арифметическое двух чисел, если a положительное и
частное (a/b) в противном случае.
Запись решения задачи на алгоритмическом языке:
алг числа
вещ a,b,c
нач
ввод a,b
если a0
то с:=(a+b)/2
иначе с:=a/b
все
вывод с
кон
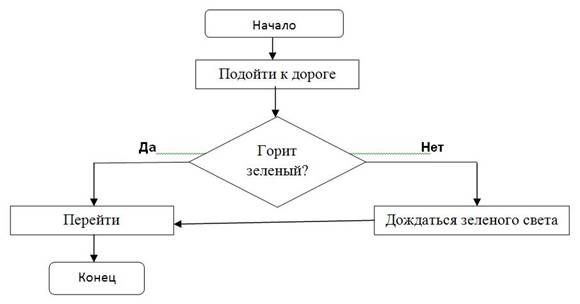
Пример 2. Составьте алгоритм для перехода дороги на светофоре.

Рис. 2. Светофор (Источник).
Решение:
Возможны следующие ситуации: в тот момент, когда мы подошли к дороге горел красный или зелёный свет. Если горел зелёный свет, то можно переходить дорогу. Если же горел красный свет, то необходимо дождаться зелёного – и уже тогда переходить дорогу.
Таким образом, алгоритм имеет следующий вид:
Подойти к светофору.
Посмотреть на его свет.
Если горит зелёный, то перейти дорогу.
Если горит красный, то подождать, пока загорится зелёный, и уже тогда перейти дорогу.
Блок-схема данного алгоритма имеет вид:
Пример 3. Составить алгоритм перевода чисел из десятичной системы в двоичную.
Решение:
То есть, алгоритм будет выглядеть так:
Если число равно 0 или 1, то это и будет его двоичное представление.
Если число больше 1, то мы делим его на 2.
Полученный остаток от деления записываем в последний разряд двоичного представления числа.
Если полученное частное равно 1, то его дописываем в первый разряд двоичного представления числа и прекращаем вычисления.
Если же полученное частное больше 1, то мы заменяем исходное число на него и возвращаемся в пункт 2).
Блок-схема этого алгоритма выглядит следующим образом:
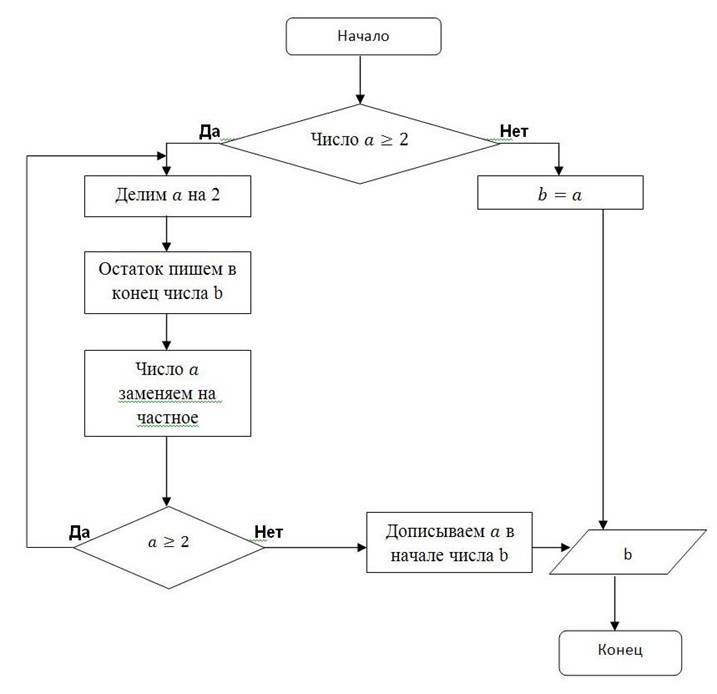
Рис. 4. Блок-схема к примеру 3.
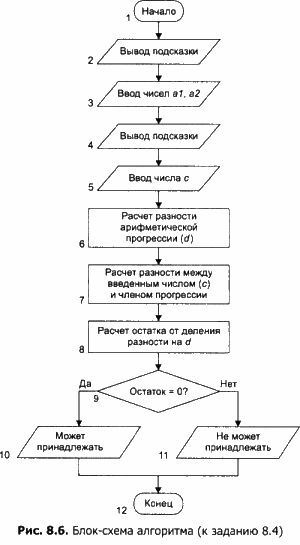
Требуется разработать алгоритм проверки принадлежности введенного числа данной арифметической прогрессии. Прогрессия задается двумя последовательными членами.
Словесный алгоритм
Начало алгоритма
1. Введите два последовательных члена арифметической прогрессии.
2. Введите произвольное целое число.
3. Найдите разность (d) арифметической прогрессии.
4. Найдите разность между введенным числом и членом арифметической прогрессии.
5. Найдите остаток от деления нацело найденной разности на d.
6. Организуйте проверку остатка:
- если остаток от деления равен 0, выведите сообщение:
«Число принадлежит рассматриваемой арифметической прогрессии»;
- иначе выведите сообщение:
«Число не принадлежит рассматриваемой арифметической прогрессии».
Конец алгоритма
Алгоритм в виде блок-схемы
Практическая работа №7
Циклический алгоритм. Определение. Блок- схема. Цикл «До» цикл «пока» цикл с параметром
Большинство практических задач требует многократного повторения одних и тех же действий, т. е. повторного использования одного или нескольких операторов.
Пусть требуется ввести и обработать последовательность чисел. Если чисел всего пять, можно составить линейный алгоритм. Если их тысяча, записать линейный алгоритм можно, но очень утомительно и нерационально. Если количество чисел к моменту разработки алгоритма неизвестно, то линейный алгоритм принципиально невозможен.
Другой пример. Чтобы найти фамилию человека в списке, надо проверить первую фамилию списка, затем вторую, третью и т.д. до тех пор, пока не будет найдена нужная или не будет достигнут конец списка. Преодолеть подобные трудности можно с помощью циклов.
Циклом называется многократно исполняемый участок алгоритма (программы). Соответственно циклический алгоритм — это алгоритм, содержащий циклы.
Различают два типа циклов: с известным числом повторений и с неизвестным числом повторений. При этом в обоих случаях имеется в виду число повторений на стадии разработки алгоритма.
Существует 3 типа циклических структур:
Цикл с предусловием;
Цикл с постусловием;
Цикл с параметром;
Иначе данные структуры называют циклами типа «Пока», «До», «Для».
Графическая форма записи данных алгоритмических структур:
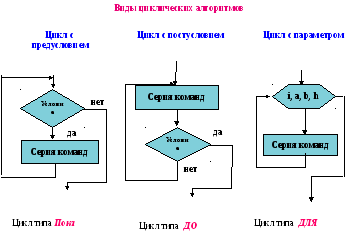
Цикл с предусловием (иначе цикл пока) имеет вид:
| Форматы записи операторов алгоритма | Блок-схема | Форматы записи операторов на Паскале |
| Пока (условие) нц серия команд кц
| 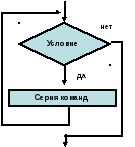
| while условие do begin серия команд; end;
|
где
условие – выражение логического типа.
Цикл может не выполняться ни разу, если значение логического выражения сразу же оказывается ложь.
Студент в первый день выучил 5 английских слов. В каждый следующий день он выучивал на 2 слова больше, чем в предыдущий. Сколько английских слов.
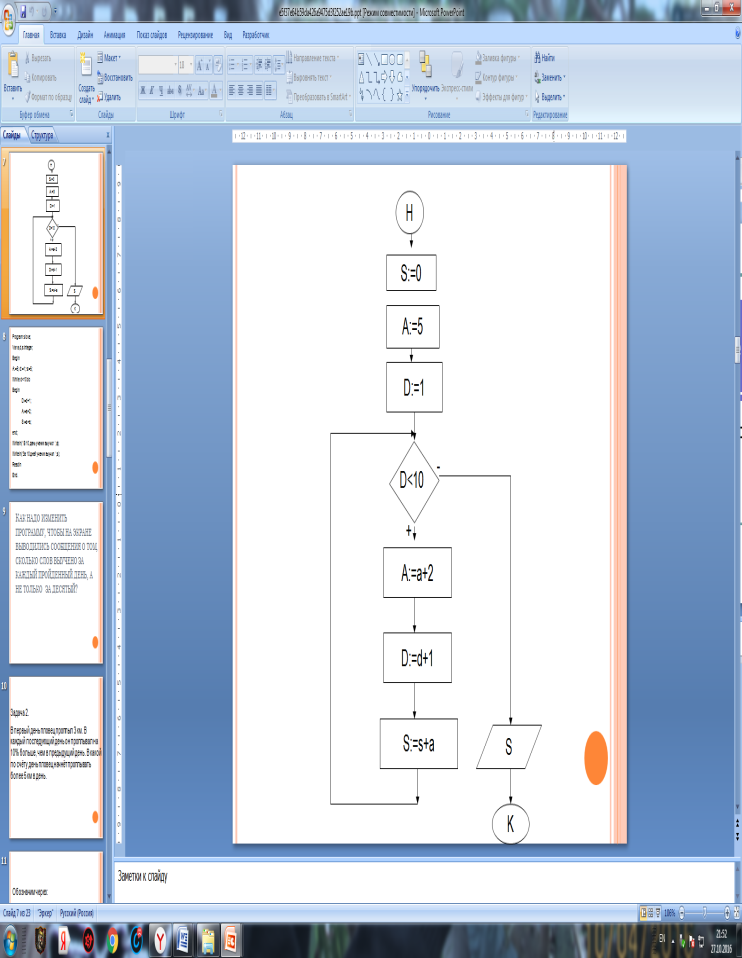
Program slova;
Var a,d,s:integer;
Begin
A:=5; d:=1; s:=5;
While d
Begin
D:=d+1;
A:=a+2;
S:=s+a;
end;
Writeln(‘ В 10 день ученик выучил ‘,a);
Writeln(‘За 10 дней ученик выучил ‘,s);
Readln
End.
Серия команд, находящихся между begin и end, выполняются до тех пор, пока условие истинно.
Для того чтобы цикл завершился, необходимо, чтобы последовательность инструкций между BEGIN и END изменяла значение переменных, входящих в условие.
Цикл с параметром (иначе цикл для) имеет вид:
| Форматы записи операторов алгоритма | Блок-схема | Форматы записи операторов на Паскале |
| Для i от а до b шаг h делай Нц Серия команд кц
| 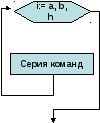
| h = +1 for i:= a to b do begin серия команд end; h = -1 for i:= b downto a do begin Cерия команд; end; |
где
i- параметр цикла;
a – начальное значение цикла;
b- конечное значение цикла;
h-шаг изменения параметра.
Структура данного цикла иначе называют циклом i раз.
Эта команда выполняется таким образом: параметру i присваивается начальное значение а, сравнивается с конечным значением b и, если оно меньше или равно конечному значению b, выполняется серия команд. Параметру присваивается значение предыдущего, увеличенного на величину h - шага изменения параметра и вновь сравнивается с конечным значением b.
Практическая работа №8
Вспомогательные алгоритмы. Процедуры. Составление простейших алгоритмов и запись их в графическом виде.
В некоторых алгоритмах есть блоки, которые многократно повторяются в разных частях алгоритма. В соответствии с правилами программирования эти блоки можно объединить в подпрограмму (вспомогательный алгоритм).
Вспомогательный алгоритм – это алгоритм решения некоторой подзадачи из основной задачи. (Учащиеся записывают определение с доски).
Вс помогательный алгоритм требует:
помогательный алгоритм требует:
Объявления;
Определения (описания);
Вы зова (обращения). Для вызова подпрограммы будем использовать блок . В нем записывается имя подпрограммы и в круглых скобках ее параметры, сначала аргументы, затем результат.
зова (обращения). Для вызова подпрограммы будем использовать блок . В нем записывается имя подпрограммы и в круглых скобках ее параметры, сначала аргументы, затем результат.
Метод программирования, при котором сначала записывается основной алгоритм, а затем описываются использованные в нем вспомогательные алгоритмы, называется методом последовательной детализации или программирование сверху вниз. Обратный порядок – снизу вверх.
Использование вспомогательных алгоритмов имеет ряд достоинств. Запишите их в тетрадь:
Сокращает алгоритм за счет отсутствия многократных описаний одних и тех же повторяющихся действий.
Облегчает понимание текста в алгоритме.
Обучает исполнителя новым предписаниям, то есть расширяет его СКИ.
Позволяет свести новую задачу к уже решенным.
Позволяет составлять, проверять и исправлять большие алгоритмы по частям.
Позволяет решить трудную задачу, разбивая ее на мелкие подзадачи.
Ра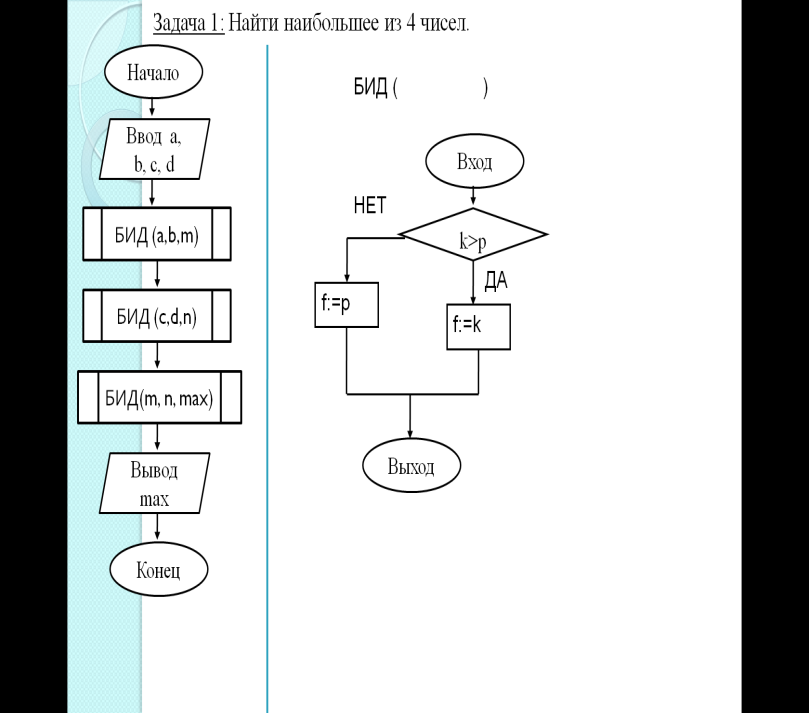 ссмотрим пример задачи (на доске). Запишите ее условие. Алгоритм появляется по частям лишь в ходе решения.
ссмотрим пример задачи (на доске). Запишите ее условие. Алгоритм появляется по частям лишь в ходе решения.
Я предлагаю вам использовать для ее решения вспомогательный алгоритм. Начнем алгоритм с ввода четырех чисел. Суть решения задачи сводится к тому следующему: возьмем первые два числа, найдем максимальное из них, затем найдем максимальное из двух последних чисел. После этого у нас имеется два максимальных числа, нам нужно лишь найти максимум из них. Из этого видно, что мы три раза находим максимальное из двух чисел, это и будет выполнять наш вспомогательный алгоритм. Запишем сначала основной алгоритм. Как мы уже поняли, используем три раза вспомогательный алгоритм. Вызов отличается только параметрами.
После того, как основной алгоритм написан, создадим вспомогательный алгоритм – БИД.
В основном алгоритме мы использовали фактические параметры. При описании подпрограммы будем использовать формальные параметры, они могут отличаться от фактических по имени, но должны четко следовать порядку фактических и их количеству.
Возьмем в качестве формальных параметров k, p, f. При первом вызове подпрограммы параметр k примет значение a, при втором вызове – c.
Составим сам вспомогательный алгоритм. Он отличается от основного в первую очередь тем, что начинается с блока – ВХОД. В теле подпрограммы используем разветвляющийся алгоритм для определения максимального числа. При окончании используется блок ВЫХОД, при первом вызове результат из фактического параметра f поместится в фактический параметр m.
Теперь составим таблицу трассировки для того, чтобы усвоить принцип действия данного алгоритма. (На доске составляем таблицу и подробно комментируем ее выполнение).
[Использован третий и четвертый методические приемы, способствующие развитию второго, четвертого и пятого компонентов алгоритмического мышления].
Решим другую задачу: треугольник задан координатами своих вершин. Найти периметр треугольника.
Сначала вспомним формулы для вычисления периметра треугольника. Для этого нужны формулы нахождения длин сторон по вершинам треугольника. Поскольку нам нужно найти длину трех длин, будем использовать вспомогательный алгоритм.
Теперь попробуем воспользоваться методом снизу вверх, т. е. сначала составим вспомогательный алгоритм, а затем основной.
Назовем вспомогательный алгоритм ДЛИНА.
ДЛИНА (I,j,k,l,m);
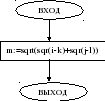
Параметр m является результатом, а все остальные параметры - аргументы.
Этот вспомогательный алгоритм мы будем использовать в основном алгоритме.


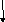
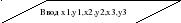
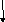
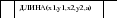
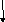
P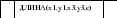 := a+b+c
:= a+b+c
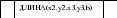

[Использована часть четвертого методического приема, способствующая развитию второго и четвертого компонентов алгоритмического мышления].
Домашнее задание.
Повторить тему «Алгоритмы и исполнители».
Составить алгоритм, в результате которого величина А меняется значением с величиной B, а величина C с величиной D. Использовать вспомогательный алгоритм, осуществляющий обмен значениями двух переменных.
Подумайте, как можно произвести перестановку двух переменных?
Если мы переместим одну в другую, то безвозвратно потеряем одно значение. Поэтому воспользуемся стандартным алгоритмом перестановки. Для этого нужно завести третью переменную и поместить туда переменную А. После этого мы можем поместить значение переменной B в ячейку A и затем в ячейку B значение дополнительной переменной.
Практическая работа №9
Тема Написание профессиональных алгоритмов с помощью блок – схем: линейных, циклических и разветвляющих
Цель урока: закрепление и расширение знаний по разветвляющимся и циклическим алгоритмам, знакомство с видами циклических структур.
Задачи урока:
формирование алгоритмического подхода к решению задач;
расширить и углубить представления об алгоритмах;
расширение понятий об алгоритмических структурах;
научиться реализовывать основные алгоритмические конструкции с помощью блок-схем;
Понимать сущность и социальную значимость своей профессии, проявлять к ней устойчивый интерес (ОК 1).
Организовывать собственную деятельность исходя из целей и способов её достижения, определенных руководителем (ОК 2).
Осуществлять поиск информации, необходимой для эффективного выполнения профессиональных задач (ОК4).
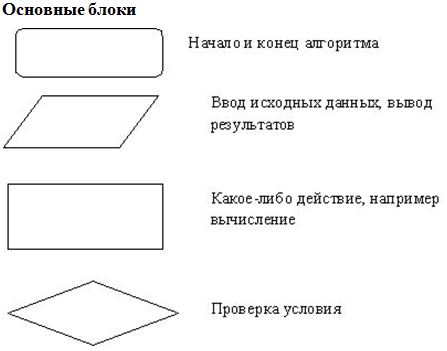
Примеры определения результата выполнения алгоритма по заданной блок-схеме.
Пример 1.
Дана блок-схема алгоритма
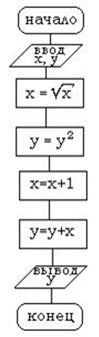
Определить результат выполнения алгоритма при определённых значениях исходных данных
Например, при x=16 и y=2
Ввод: х=16 y=2
x=16=4
y=y2=4
x=4+1=5
y=4+5=9
Вывод: y=9
Пример 2.
Дана блок-схема алгоритма
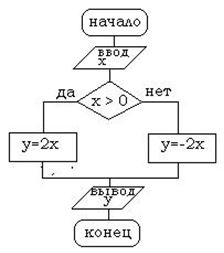
Определить результат выполнения алгоритма при определённых значениях исходных данных
Например, при x= –6 или x=0 или x=7
1) Ввод: х= –6
Проверка условия x0 «Нет» y= –2*(–6)=12
Вывод: y=12
2) Ввод: х=0
Проверка условия x0 «Нет» y= –2*0=0
Вывод: y=0
3) Ввод: х=7
Проверка условия x0 «Да» y=2*7=14
Вывод: y=14
Пример 3.
Дана блок-схема алгоритма
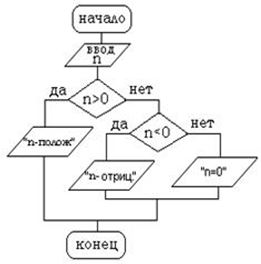
Определить результат выполнения алгоритма при определённых значениях исходных данных
Например, при n=15 или n=0 или n= –7
1) Ввод: n=15
Проверка условия n0 «Да» Вывод «n-положительное»
2) Ввод: n=0
Проверка условия n0 «Нет» Проверка условия nn=0»
3) Ввод: n= –7
Проверка условия n0 «Нет» Проверка условия n
«n-отрицательное»
Пример 4.
Дана блок-схема алгоритма
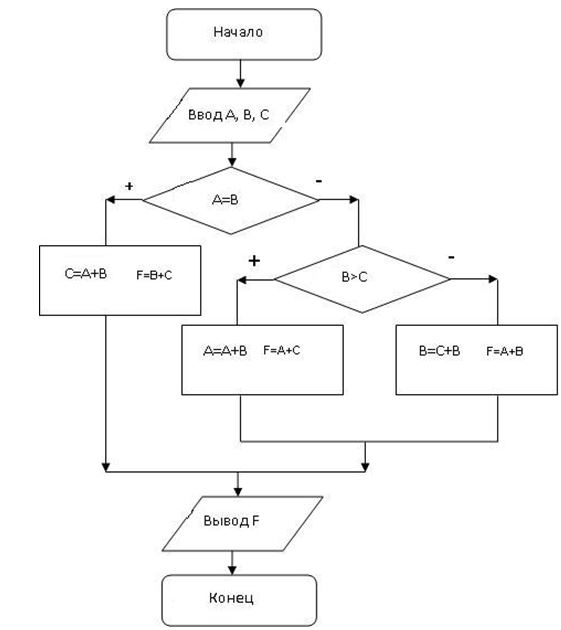
Определить результат выполнения алгоритма при определённых значениях исходных данных
Например, при A=7; B=8; C=9 или A=6; B=6; C= –10 или A=6; B=10; C= –10
1) Ввод: A=7; B=8; C=9
Проверка условия A=B «Нет» Проверка условия BC «Нет» B=9+8=17; F=7+17=24 Вывод F=24
2) Ввод: A=6; B=6; C= –10
Проверка условия A=B «Да» С=6+6=12; F=6+12=18 Вывод F=18
3) Ввод: A=6; B=10; C= –10
Проверка условия A=B «Нет» Проверка условия BC «Да» A=6+10=16; F=16+(–10)=6 Вывод F=6
Пример 5.
Дана блок-схема алгоритма
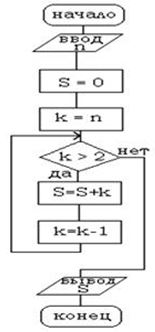
Определить результат выполнения алгоритма при определённых значениях исходных данных
Например, при n=4 или n=1
1) Ввод: n=4
S=0
k=4
Проверка условия k2 «Да» S=0+4=4; n=4–1=3
Проверка условия k2 «Да» S=4+3=7; n=3–1=2
Проверка условия k2 «Нет» Вывод S=7
2) Ввод: n=1
S=0
k=1
Проверка условия k2 «Нет» Вывод S=0
Практическая часть
1. Составить блок-схемы:
Линейный алгоритм
Вычисление площади прямоугольника.
Вычисление суммы четырех чисел.
Вычисление произведения трёх чисел.
Вычисление площади треугольника.
Вычисление частного двух чисел.
Вычисление длины окружности.
Вычисление площади круга.
Вычисление площади квадрата.
Вычисление площади параллелограмма.
Вычисление заданных двух чисел 20 и 18.
Ветвление
По форме фигуры определить, какая фигура: “квадрат”, “окружность”.
Определить виды предложений.
Найти значение функции  .
.
Дополнительное задание (составить блок-схемы):
Пешеход шел по пересеченной местности. Его скорость движения по равнине v1 км/ч, в гору — v2 км/ч и под гору — v3 км/ч. Время движения соответственно t1, t2 и t3 ч. Какой полный путь прошел пешеход?
Решение квадратного уравнения.
2. Работа за компьютером 1) Составить алгоритм в программе MS WORD (напечатать).
Контрольные вопросы:
Понятие алгоритма.
Свойства алгоритмов.
Формы записей алгоритмов.
Общие принципы построения алгоритмов.
Основные алгоритмические конструкции: линейные, разветвляющиеся, циклические. Данные: понятие и типы.
Основные базовые типы данных и их характеристика.
Структурированные типы данных и их характеристика.
Методы сортировки данных.







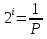

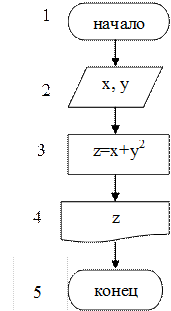












 помогательный алгоритм требует:
помогательный алгоритм требует: ссмотрим пример задачи (на доске). Запишите ее условие. Алгоритм появляется по частям лишь в ходе решения.
ссмотрим пример задачи (на доске). Запишите ее условие. Алгоритм появляется по частям лишь в ходе решения.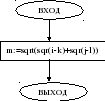
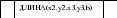






 .
.









