Правила дифференцирования.
Определим правила, по которым можно находить производные суммы (или разности), произведения и частного.
Пусть 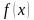 и
и  определены и непрерывны на всей своей области определения. Найдём производную суммы этих двух функций:
определены и непрерывны на всей своей области определения. Найдём производную суммы этих двух функций:  .
.
По определению производной,




Аналогично выводится формула для нахождения производной разности.
Значит, 
Теперь найдём производную произведения двух функции 





Значит, 
Производная произведения двух функций равна производной первой функции, умноженной на вторую функцию, плюс производная второй функции, умноженная на первую.
Найдём теперь производную частного двух функций 




Значит, 
Производная частного двух функций равна дроби, в числителе которой – разность произведения производной числителя на знаменатель и производной знаменателя на числитель, а в знаменателе – квадрат знаменателя.
Приведём примеры.

 ;
;


Рассмотрим случай, когда функция является сложной.
Определение. Если  , а
, а  , то
, то  называется сложной функцией с промежуточным аргументом
называется сложной функцией с промежуточным аргументом  и независимым аргументом
и независимым аргументом  . Здесь
. Здесь  называют внутренней функцией, а
называют внутренней функцией, а  – внешней функцией.
– внешней функцией.
Например, сложной является функция  . В ней
. В ней  – внешняя функция,
– внешняя функция,  – внутренняя функция.
– внутренняя функция.
Производная сложной функции равна произведению производной внешней функции по неизменной внутренней на производную внутренней функции.
Например, . Мы сначала взяли производную степени, а затем умножили её на производную основания степени.
Найти производную функции:
Найти значение производной в точке  :
:
Вычислите скорость изменения функции в точке  :
:
При каких значениях  выполняется равенство
выполняется равенство  , если известно, что
, если известно, что
?
При каких значениях  выполняется равенство
выполняется равенство  , если известно, что
, если известно, что
 ?
?
Решить неравенство  если:
если:
Решить уравнение  , если:
, если:
При каких значениях аргумента скорость изменения функции  равна скорости изменения функции
равна скорости изменения функции  :
:
При каких значениях аргумента скорость изменения функции  больше скорости изменения функции
больше скорости изменения функции  , если: ?
, если: ?
Зависимость расстояния  от времени
от времени  движущейся точки такова:
движущейся точки такова:  . Докажите, что её скорость не превосходит
. Докажите, что её скорость не превосходит 
Зависимость расстояния  от времени
от времени  движущейся точки такова:
движущейся точки такова:  . Докажите, что её скорость не превосходит
. Докажите, что её скорость не превосходит 
Найдите производную функции  , если
, если  .
.
Найдите производную функции  , если
, если  .
.
При каких значениях  производная функции
производная функции  отрицательна?
отрицательна?
При каких значениях  производная функции
производная функции  отрицательна?
отрицательна?
Сила тока  изменяется в зависимости от времени
изменяется в зависимости от времени  по закону
по закону  , где
, где  – сила тока в амперах,
– сила тока в амперах,  – время в секундах. Найти скорость изменения силы тока в конце указанной секунды, если:
– время в секундах. Найти скорость изменения силы тока в конце указанной секунды, если:
Найти производную функции:
Найти значение производной функции 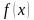 в точке
в точке  :
:
Найти значение выражения:
 , где
, где 
 , где
, где 
Решить данные уравнения и неравенства:
 , где
, где
 , где
, где
 , где
, где
 , где
, где
 , где
, где
3







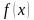 и
и  определены и непрерывны на всей своей области определения. Найдём производную суммы этих двух функций:
определены и непрерывны на всей своей области определения. Найдём производную суммы этих двух функций:  .
.


















 ;
;


















