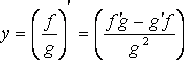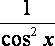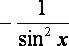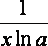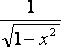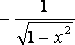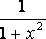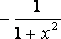| Тема: Правила нахождения производных. Цели: ознакомить учащихся с правилами вычисления производных, формулой вычисления производной степенной функции; научить использовать их при решении примеров, расширить знания о производной. Ход урока I. Организационный момент. Организация класса в течение всего урока, готовность учащихся к уроку, порядок и дисциплина. Постановка целей учения перед учащимися, как на весь урок, так и на отдельные его этапы. II. Объяснение нового материала: По знаку производной можно судить о направлении изменения функции: если производная положительна, функция растет, если производная отрицательна, функция убывает. Если производная равна нулю, то функция не растет и не убывает. В случае нелинейной функции это означает, что в точке, где производная равна нулю, функция имеет минимум или максимум (математики часто говорят "экстремум" вместо "минимум или максимум"). (Рис.11.) 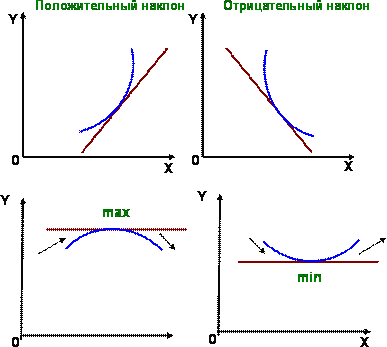
Рис.11. Правила нахождения производных Если нам известна исходная функция, мы можем отыскать по ней ее производную. В алгебре существует достаточно много правил отыскания производных, илидифференцирования. Если с - постоянное число, и f(x), g(x) - некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования: | Правило константы | y = C = y' = 0 y = (Cf)' = C (f)' | | Правило суммы | y = f(x) + g(x) = y' = f '(x) + g'(x) | | Правило умножения | у = ( fg )' = f 'g+g'f | | Правило деления | 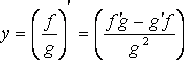
| | Правило сложной функции | если y = f(x), u = g(y), то функция u =g(f(x)) - сложная функция, или суперпозиция. u' = g(f(x))' = g'(y)*f '(x) | | Обратная функция | если для функции y = f(x) существует обратнаядифференцируемая функции x = f -1(y), то она тоже имеет производную в соответствующей точке: (f -1(y))у=у0 =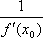 | На основе определения производной и правил дифференцирования можно составить список производных основных элементарных функций. | f(x) | f '(x) | f(x) | f '(x) | | С | 0 | sin x | cos x | | ха | аха-1 | cos x | – sin x | | ах | ахlna | tg x | 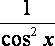
| | ех | ех | ctg x | 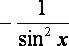
| | log a x | 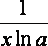
| arcsin x | 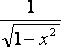
| | | | arccos x | 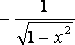
| | | | arctg x | 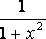
| | | | arcctg x | 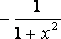
| Кроме правил для нахождения производных нужно помнить следующие правила: 1. переменная без показателя степени – это переменная в первой степени (x = x1); 2. переменная в нулевой степени – это единица (x0 = 1). Например, найти производную функции: y = x2 + 3x - 10 y' = (x2 + 3x – 10)' = (x2 )'+ (3x)' – 10'=2x2-1 + 3x1-1 - 0 = 2x1 + 3x0 = 2 |