ОГБПОУ «НОВГОРОДСКИЙ АГРОТЕХНИЧЕСКИЙ ТЕХНИКУМ»
Инструкционная карта на выполнение
Практического занятия № 3 по дисциплине
«Математика»
Тема: Пределы и непрерывность
Наименование работы:. Вычисление пределов в точке и на бесконечности. Замечательные пределы
| Наименование объектов контроля и оценки | Основные показатели оценки результата |
| Умения: Решать прикладные задачи в области профессиональной деятельности. Знания: Значение математики в профессиональной деятельн ости и при освоении ППССЗ; Основные математические методы решения прикладных задач в области профессиональной деятельности; Основы интегрального и дифференциального исчисления | Оценка результатов выполнения практических работ
|
Норма времени: 6 часов;
Условия выполнения: учебный кабинет;
Оснащение рабочего места: инструкционная карта, калькулятор
Правила по технике безопасности: С правилами техники безопасности на рабочем месте ознакомлены;
Литература: Хрипунова М.Б. Высшая математика. Учебник и практикум для спо М.:Юрайт.2018г.-474с
Уровни усвоения: 1 – 4 задания – 2 уровень
Домашнее, самостоятельное задание – 3 уровень
Теоретическая часть.
Предел бесконечности
Определение: Постоянная величина а называется пределом переменной х, если модуль разности 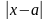 при изменении х становится и остается меньше любого как угодно малого положительного числа
при изменении х становится и остается меньше любого как угодно малого положительного числа 
 или
или 
Замечание: Предел постоянной величины равен самой постоянной величине: 
Определение: Последовательность называется бесконечно малой, если ее предел равен нулю.
Последовательность называется бесконечно большой, если ее предел равен бесконечности.
Если последовательность  – бесконечно большая, то последовательность
– бесконечно большая, то последовательность  бесконечно малая, и наоборот.
бесконечно малая, и наоборот.
Свойства пределов:



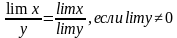

Предел функции в точке
Пусть даны две переменные величины х и у, такие, что у=f(х)
Определение: Число b называется пределом функции f(x) в точке а, если для всех значений х, достаточно близких к а, значение функции f(x) сколь угодно мало отличается от числа b.

Примеры. Вычислить пределы функций в точке:




Чтобы разложить числитель на множители, найдем корни квадратного уравнения:





Предел функции на бесконечности.
Определение: число А называется пределом функции у=f(x) на бесконечности, если для всех достаточно больших по модулю значений аргумента х соответствующие значения функции f(x) сколь угодно мало отличаются от числа А.

Примеры. Вычислить пределы функций на бесконечности:
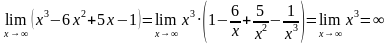
(Так как  )
)
Замечательные пределы
 =1 - 1-й замечательный предел
=1 - 1-й замечательный предел
- 2-й замечательный предел
Примеры. Вычислить пределы:
Практическая часть.
Вычислить пределы функций в точке:
а) б)  в)
в)  г)
г) 
д) е)  ж) з)
ж) з)
Вычислить пределы функции на бесконечности:
а) б) в)  г)
г)
д) е)
Вычислить замечательные пределы:
а)  б) в) г)
б) в) г)
д) е) ж) е)
ж) з) и)
Вычислить пределы:
а) б)  в)
в)
г) д) е)
д) е) ж)
домашнее задание:
Вычислить пределы функций в точке и на бесконечности:
а)  б) в)
б) в)
Вычислить пределы:
а) б) в)
Самостоятельная работа:
| 1 вариант
| 2 вариант

|
Критерии оценки:
«5» - Правильно решены все пять заданий. Возможна 1 вычислительная ошибка;
«4» - Правильно решены четыре задания, возможна одна вычислительная ошибка, либо выполнены все пять заданий, но допущены 2 вычислительные ошибки;
«3» - Правильно решены три задания, возможна одна вычислительная ошибка; либо выполнено 4-5 заданий, но допущено 3 ошибки.
«2» - Правильно сделано менее трех заданий







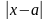 при изменении х становится и остается меньше любого как угодно малого положительного числа
при изменении х становится и остается меньше любого как угодно малого положительного числа 
 или
или 

 – бесконечно большая, то последовательность
– бесконечно большая, то последовательность  бесконечно малая, и наоборот.
бесконечно малая, и наоборот.


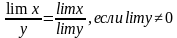












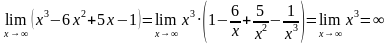
 )
)









