Занятие 19. Тема «Предикаты и операции над ними. Кванторы»
План лекции:
Понятие предиката
Основные множества для предикатов
Операции над предикатами
Кванторы. Операции навешивания квантора
Понятие предиката
В дискретной математике, как и в математической теории, основными неопределяемыми понятиями являются понятия суждение, истина, ложь. Суждение не может быть одновременно истинным и ложным. Например, все предложения, которые произносит человек, являются суждениями. Суждение, зависящее от переменной величины, которое при подстановке значений переменного становится высказыванием, называют предикатом. Для описания внутренней логической структуры простых высказываний используется понятие предиката. Сегодня мы изучим основные понятия предикатов, рассмотрим операции, совершаемые с предикатами.
Определение. Предложения, содержащие переменные, истинность или ложность которого зависит от значения переменного, входящего в него, называется предикатом. Другими словами, это функция, заданная на определенном множестве. Обозначение Р(х), Р(х,у), …, Р(х1,х2, …,хn).
Пример. Высказывание А=«Волк – это хищник»
Предикат Р(х)=«х – это хищник». Истинность Р(х) будет зависеть от того, что поставить вместо х, т.е. если поставим х=Лиса, то получим истину, а если поставим х=Коза, то получим ложь.
Основные множества для предикатов
Считается, что с каждым предикатом задано множество, из которого выбирают значение переменных. Такое множество называют областью определения предиката. Обозначение D(P).
Пример. Р(х)=«х+3 . Какое бы число не поставить вместо х, будем получать либо ложное либо истинное высказывание.

Подмножеством области определения предиката, на котором он принимает значение истинность, называется множеством истинности данного предиката. Обозначение М(Р). М(Р) 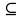 D(P).
D(P).
Пример для Р(х)=«х+3
Значит, М(Р)=(-∞;3)
Операции над предикатами
Все операции будем рассматривать на примере Р(х)=«х-число, делящееся на 9», K(х)=«х-цифра». Для выполнения операций, нужно найти область определения предиката и множество истинности предиката и расписать эти множества как множество с перечислением элементов (с этого нужно начинать практическую), то есть
Для предиката Р(х)=«х-число, делящееся на 9»
D(P) ={1,2,3,4,5…95,96,97,98,…} М(Р) ={9,18,27,36,…,81,90,99,108,…}
K(х)=«х-цифра» D(К) ={1,2,3,4,5,6,7,8,9} М(К)={0,1,2,3,4,5,6,7,8,9}
Отрицанием предиката Р(х) называется новый предикат 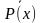 , определённый на множестве D(Р) и истинный при тех значениях переменных х, при которых предикат Р(х) ложен.
, определённый на множестве D(Р) и истинный при тех значениях переменных х, при которых предикат Р(х) ложен.
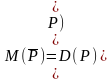
Пример. 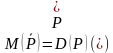 ={1,2,3,4,5…95,96,97,98,…}\ {9,18,27,36,…,81,90,99,108,…}={1,2,3,4,5,6,7,8,10,11,12,…,}то есть убрать из D(P) все числа, делящиеся на 9.
={1,2,3,4,5…95,96,97,98,…}\ {9,18,27,36,…,81,90,99,108,…}={1,2,3,4,5,6,7,8,10,11,12,…,}то есть убрать из D(P) все числа, делящиеся на 9.
Конъюнкцией двух предикатов Р(х) и Q(x) называется новый предикат Р(х)⋀Q(x), определённый на множестве D(Р) и истинный при тех значениях переменных х, при которых истины одновременно оба предиката P(x) и Q(x).
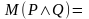
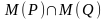
Пример. 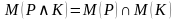 ={9,18,27,36,…,81,90,99,108,…}
={9,18,27,36,…,81,90,99,108,…}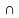 {0,1,2,3,4,5,6,7,8,9}= {9}
{0,1,2,3,4,5,6,7,8,9}= {9}
Дизъюнкцией двух предикатов Р(х) и Q(x) называется новый предикат Р(х)VQ(x), определённый на множестве D(Р) и истинный при тех значениях переменных х, при которых истинен хотя бы один из предикатов P(x) и Q(x).
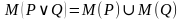
Пример.
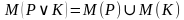 ={9,18,27,36,…,81,90,99,108,…}
={9,18,27,36,…,81,90,99,108,…}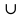 {0,1,2,3,4,5,6,7,8,9}=
{0,1,2,3,4,5,6,7,8,9}=
{0,1,2,3,4,5,6,7,8,9,18,27,36,…,81,90,99,108,…}
Импликацией двух предикатов Р(х) и Q(x) называется новый предикат Р(х)  Q(x), определённый на множестве D(Р) и ложный при тех значениях переменных х, при которых предикат P(x) истинен, а предикат Q(x) ложен.
Q(x), определённый на множестве D(Р) и ложный при тех значениях переменных х, при которых предикат P(x) истинен, а предикат Q(x) ложен.
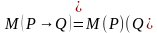
Пример. 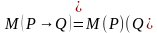 ={9,18,27,36,…,81,90,99,108,…}\ {0,1,2,3,4,5,6,7,8,9} = {18,27,36,45,…,81,90,99,108,…}
={9,18,27,36,…,81,90,99,108,…}\ {0,1,2,3,4,5,6,7,8,9} = {18,27,36,45,…,81,90,99,108,…}
Эквиваленцией двух предикатов Р(х) и Q(x) называется новый предикат Р(х) ↔ Q(x), определённый на множестве D(Р) и истинный при тех значениях переменных х, при которых либо оба предиката истины, либо оба предиката ложны.
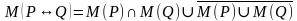
Пример.
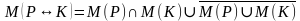 ={9,10,11,12,13,14,15,16,17,19,…}
={9,10,11,12,13,14,15,16,17,19,…}
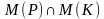 = {9},
= {9},
 = {0,1,2,3,4,5,6,7,8,9,18,27,36,…,81,90,99,108,…}
= {0,1,2,3,4,5,6,7,8,9,18,27,36,…,81,90,99,108,…}
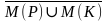 ={10,11,12,13,14,15,16,17,19,…}
={10,11,12,13,14,15,16,17,19,…}
Кванторы. Операции навешивания квантора
Для количественных характеристик обычно используют понятия «все», «некоторые», «существуют» и др. В математике эти слова называются кванторами. От латинского слова quantum – сколько.
Операция, сопоставляющая предикату Р(х) высказывание «Для любого х имеет место Р(х)» - истинное, если М(Р) совпадает с D(Р), называется операцией навешивания квантора общности. Обозначается 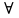 - любой или
- любой или 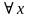 - для каждого, для любого, для всякого
- для каждого, для любого, для всякого
Пример: если Р(х): «х+3=8» не известно истина оно или ложь, не подставляя значения, то (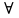 х
х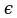 R)( х+3=8) – ложь. Читается это так «Для любого числа х из множества действительных чисел выполняется равенство х+3=8»-ложь
R)( х+3=8) – ложь. Читается это так «Для любого числа х из множества действительных чисел выполняется равенство х+3=8»-ложь
Операция, сопоставляющая предикату Р(х) высказывание «Существует х для Р(х)» - истинное, если М(Р)≠ǿ, называется операцией навешивания квантора существования. Обозначается  - существует или
- существует или  - найдется х, существует х, для некоторого х.
- найдется х, существует х, для некоторого х.
Пример: если Р(х): «х+3=8» не известно истина оно или ложь, не подставляя значения, то ( х
х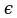 R)( х+3=8) – истинно. Читается это так «Существует такое число х из множества действительных чисел, для которого выполняется равенство х+3=8»-истино.
R)( х+3=8) – истинно. Читается это так «Существует такое число х из множества действительных чисел, для которого выполняется равенство х+3=8»-истино.
Предикатная формула – это формула, содержащая знаки булевых операций и кванторов, то есть в формуле участвуют: символы предметных переменных, символы предикатов, логические символы и символы кванторов.
Задания для самостоятельной работы
Объяснить, почему следующие выражения имеют значение истина или ложь, описать выражения словами
Для следующих предложений выделить предикаты и для каждого из них указать область истинности:
х+5=1;
х+2
однозначное число х кратно 3;
Пусть х определен на множестве людей М, а Р(х) – предикат «х – смертен». Дать словесную формулировку предикатной формулы 
Пусть Р(х) – предикат «х – четное число», определенный на множестве М. Дать словесную формулировку высказыванию  , определить его истинность.
, определить его истинность.
На множестве M = {3, 6, 9, 12, 42} определены предикаты: P(x) - "число Х делится на 6" и Q(x) - "число Х  30". Найдите область истинности предикатов
30". Найдите область истинности предикатов  ,
,  ,
,  ,
,  ,
, 
Запишите приведенные ниже утверждения в символической форме, введя предикаты. В случае необходимости укажите предметную область.
а) Некоторые машины умнее людей.
б) Любой играет в теннис лучше Фрэда.
в) Для каждого действует существует равное и противоположно направленное противодействие.
г) Каждый игрок в гольф, в конце концов, будет обыгран более сильным игроком
Пользуясь этим и теоретическим материалом учебника М.С. Спирина «Дискретная математика» глава 5 п.5.3 стр.224, выполнить все задания.
Выполненное задание отправить на адрес https://vk.com/id52519522 в виде фото, сделанное из тетради.








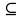 D(P).
D(P).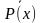 , определённый на множестве D(Р) и истинный при тех значениях переменных х, при которых предикат Р(х) ложен.
, определённый на множестве D(Р) и истинный при тех значениях переменных х, при которых предикат Р(х) ложен.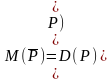
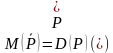 ={1,2,3,4,5…95,96,97,98,…}\ {9,18,27,36,…,81,90,99,108,…}={1,2,3,4,5,6,7,8,10,11,12,…,}то есть убрать из D(P) все числа, делящиеся на 9.
={1,2,3,4,5…95,96,97,98,…}\ {9,18,27,36,…,81,90,99,108,…}={1,2,3,4,5,6,7,8,10,11,12,…,}то есть убрать из D(P) все числа, делящиеся на 9.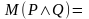
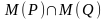
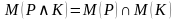 ={9,18,27,36,…,81,90,99,108,…}
={9,18,27,36,…,81,90,99,108,…}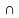 {0,1,2,3,4,5,6,7,8,9}= {9}
{0,1,2,3,4,5,6,7,8,9}= {9} 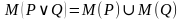
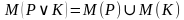 ={9,18,27,36,…,81,90,99,108,…}
={9,18,27,36,…,81,90,99,108,…}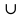 {0,1,2,3,4,5,6,7,8,9}=
{0,1,2,3,4,5,6,7,8,9}= Q(x), определённый на множестве D(Р) и ложный при тех значениях переменных х, при которых предикат P(x) истинен, а предикат Q(x) ложен.
Q(x), определённый на множестве D(Р) и ложный при тех значениях переменных х, при которых предикат P(x) истинен, а предикат Q(x) ложен.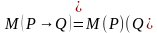
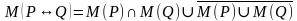
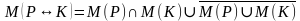 ={9,10,11,12,13,14,15,16,17,19,…}
={9,10,11,12,13,14,15,16,17,19,…}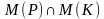 = {9},
= {9}, = {0,1,2,3,4,5,6,7,8,9,18,27,36,…,81,90,99,108,…}
= {0,1,2,3,4,5,6,7,8,9,18,27,36,…,81,90,99,108,…}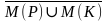 ={10,11,12,13,14,15,16,17,19,…}
={10,11,12,13,14,15,16,17,19,…}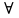 - любой или
- любой или 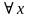 - для каждого, для любого, для всякого
- для каждого, для любого, для всякого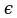 R)( х+3=8) – ложь. Читается это так «Для любого числа х из множества действительных чисел выполняется равенство х+3=8»-ложь
R)( х+3=8) – ложь. Читается это так «Для любого числа х из множества действительных чисел выполняется равенство х+3=8»-ложь









