| Отделение , группа ___ Семестр ___3___, курс__2____ Преподаватель Пластун СВ Предмет: “Элементы высшей математики” Т.З. Лекция № 3 Тема« МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ» |
Определение матрицы и её элементов.
Действия над матрицами.
Решение примеров.
1. Определение матрицы и её элементов.
Матрицы появились в середине XIX века в связи с практической потребностью решения различного рода задач, прежде всего связанных с исследованием систем линейных уравнений. Матрицей называется прямоугольная таблица вида
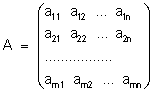
состоящая из m строк и n столбцов. Элементами матриц могут быть различные объекты (числа, функции и т.п.); мы ограничимся знакомством с некоторыми простейшими операциями над числовыми матрицами. Матрица имеет, как уже указывалось, m строк и n столбцов, говоря иначе m×n. Числа m и n могут быть любыми натуральными. Различают несколько особых случаев:
1) m=1, n 1. Матрица в этом случае называется матрицей - строкой и имеет вид

2) m 1, n=1. В этом случае матрица имеет вид 
и называется матрицей - столбцом;
3) Если m=n, то матрица называется квадратной (порядка n). В квадратной матрице выделяют главную диагональ (элементы, расположенные "на диагонали", проведенной из левого верхнего в правый нижний угол) и побочную диагональ (элементы, расположенные "на диагонали", проведенной из правого верхнего в левый нижний угол);
4) Если все элементы матрицы равны 0, то такая матрица называется нуль - матрицей и обозначается  . Часто для краткой записи матрицы употребляют обозначение
. Часто для краткой записи матрицы употребляют обозначение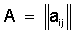
Индексы i и j определяют "адрес" элемента 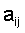 (как ряд и место в кинозале). Например, символ
(как ряд и место в кинозале). Например, символ 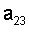 означает, что этот элемент находится во второй строке и в третьем столбце матрицы.
означает, что этот элемент находится во второй строке и в третьем столбце матрицы.
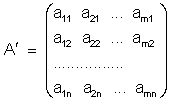
Преобразование матрицы, заключающееся в замене ее строк столбцами, называется транспонированием. Другими словами, если

то транспонированной к A матрицей будет матрица AТ
 .
.
Легко видеть, что матрица - строка транспонируется в матрицу - столбец и наоборот, порядок (m×n) матрицы при транспонировании меняется на обратный (n×m), а "двойное" транспонирование дает ту же самую матрицу
(AТ)Т=A.
Квадратная матрица порядка n называется диагональной, если все ее элементы, кроме, может быть, элементов главной диагонали равны нулю. Таким образом, матрица
 будет диагональной.
будет диагональной.
Диагональная матрица называется единичной, если все ее диагональные элементы равны 1, т.е.
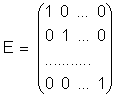 .
.
Единичная матрица является матричным аналогом единицы во множестве действительных чисел, так же как нуль - матрица - матричный аналог нуля.
Квадратная матрица, сохраняющая свой вид при транспонировании, называется симметрической. Для симметрической матрицы справедливо соотношение
AТ=A.
В симметрической матрице элементы, расположенные симметрично относительно главной диагонали одинаковы. Симметрической будет, например, любая диагональная матрица.
2. Определение основных операций над матрицами.
Матрицы A и B называются равными, если они имеют одинаковые размеры и их соответствующие элементы равны между собой. Например, матрицы 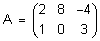 и
и 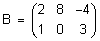 отвечают данному определению и являются равными A = B. Матрица
отвечают данному определению и являются равными A = B. Матрица  не равна ни матрице A, ни матрице B, хотя она имеет те же размеры, что и A и B и состоит из тех же элементов. Произведением матрицы A на некоторое действительное число m называется матрица mA составленная из элементов матрицы A, умноженных на число m.
не равна ни матрице A, ни матрице B, хотя она имеет те же размеры, что и A и B и состоит из тех же элементов. Произведением матрицы A на некоторое действительное число m называется матрица mA составленная из элементов матрицы A, умноженных на число m.
Из определения вытекает, что, во-первых, матрицы A и mA имеют одинаковый порядок и, во-вторых, что если все элементы некоторой матрицы имеют общий множитель, то его можно вынести за матричные скобки. Например,

Операция умножения матрицы на число подчиняется следующим простым законам:
1). mA= Am;
2). (mn)A = m(nA) = n(mA);
3). 0A = O;
4). (mA)Т = mAТ.
Суммой двух матриц A и B одного и того же порядка называется матрица C, каждый элемент которой равен сумме соответствующих элементов матриц A и B, т.е.
 .
.
Операция сложения матриц обладает следующими свойствами:
1) A + B = B + A(коммутативность);
2) (A+B)+C= A+ (B + C)(ассоциативность);
3) m(A + B) = mA + mB (дистрибутивность по отношению к умножению на действительное число);
4) O + A = A ;
5) (A + B)’ = A ’ + B’ .
Последней операцией над матрицами, которую мы рассмотрим в данном разделе, будет умножение матриц. Вначале сформулируем предварительное понятие.
Матрицы A и B (порядок следования важен!) называются согласованными, если число столбцов матрицы A равно числу строк матрицы B. Таким образом, если порядок матрицы A равен m×n , то порядок согласованной с ней матрицы B должен быть равен n×k (отметим, что квадратные матрицы одного порядка всегда согласованы).
Перемножать можно только согласованные матрицы.
Произведением двух согласованных матриц A и B называется матрица C, элементы которой рассчитываются по формуле 
Например, если требуется получить элемент 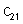 , то нужно вторую строку матрицы A "умножить" на первый столбец матрицы B. Рассмотрим конкретные матрицы
, то нужно вторую строку матрицы A "умножить" на первый столбец матрицы B. Рассмотрим конкретные матрицы
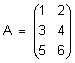 и
и 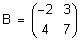 .
.
Число столбцов матрицы A и число строк матрицы B равны 2, значит, A и B согласованы.
Тогда
 .
.
Найти в этом случае произведение BA невозможно, т.к. матрицы B и A не согласованы. Отсюда следует, что операция умножения матриц, вообще говоря, не коммутативна. Можно показать, что в общем случае даже когда произведения AB и BA определены, коммутативность не выполняется.
Пусть A - матрица - строка из 3-х элементов, а B - матрица - столбец из 3-х элементов. Тогда A и B согласованы и, в результате умножения A на B получится число. Матрицы B и A также согласованы, но в результате их умножения получится квадратная матрица 3-го порядка.
Вместе с тем встречаются квадратные матрицы одного порядка, для которых выполняется коммутативность. Такие матрицы называются коммутирующими.
Отметим другие свойства умножения матриц.
1) Умножение матриц ассоциативно: (AB) C = A (BC) .
2) Умножение матриц дистрибутивно относительно сложения:
(A + B) C= AC + BC.
3) Умножение матриц коммутативно относительно умножения на действительное число:
m(AB) = (mA) B = A (mB).
4) Произведение двух матриц может быть нуль - матрицей, хотя ни один из сомножителей нуль - матрицей не является. Например,
 .
.
Таким образом, умножение двух матриц обладает некоторыми свойствами, не характерными для умножения чисел, поэтому при действиях с матрицами нужно проявлять осмотрительность и аккуратность.
3. Пример 1. Найти произведение матриц А=  и В =
и В = 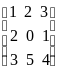 .
.
Решение. Имеем: матрица А размера 23, матрица В размера 33, тогда произведение АВ = С существует и элементы матрицы С равны
с11 = 11 +22 + 13 = 8, с21 = 31 + 12 + 03 = 5, с12 = 12 + 20 + 15 = 7,
с22 =32 + 10 + 05 = 6, с13 = 13 + 21 + 14 = 9, с23 = 33 + 11 + 04 = 10.
AB = , а произведение BA не существует.
, а произведение BA не существует.
Пример 2. В таблице указано количество единиц продукции, отгружаемой ежедневно на молокозаводах 1 и 2 в магазины М1, М2 и М3, причем доставка единицы продукции с каждого молокозавода в магазин М1 стоит 50 ден. ед., в магазин М2 - 70, а в М3 - 130 ден. ед. Подсчитать ежедневные транспортные расходы каждого завода.
| Молокозавод | Магазин |
|
| М1 | М2 | М3 |
| 1 | 20 | 35 | 10 |
| 2 | 15 | 27 | 8 |
Решение. Обозначим через А матрицу, данную нам в условии, а через
В - матрицу, характеризующую стоимость доставки единицы продукции в магазины, т.е.,
А = , В = (50, 70, 130).
Тогда матрица затрат на перевозки будет иметь вид:
АВT = .
Итак, первый завод ежедневно тратит на перевозки 4750 ден. ед., второй - 3680 ден.ед.
Пример 3. Швейное предприятие производит зимние пальто, демисезонные пальто и плащи. Плановый выпуск за декаду характеризуется вектором X = (10, 15, 23). Используются ткани четырех типов Т1, Т2, Т3, Т4. В таблице приведены нормы расхода ткани (в метрах) на каждое изделие. Вектор С = (40, 35, 24, 16) задает стоимость метра ткани каждого типа, а вектор P = (5, 3, 2, 2) - стоимость перевозки метра ткани каждого вида.
| Изделие | Расход ткани |
|
| Т1 | Т2 | Т3 | Т4 |
| Зимнее пальто | 5 | 1 | 0 | 3 |
| Демисезонное пальто | 3 | 2 | 0 | 2 |
| Плащ | 0 | 0 | 4 | 3 |
1. Сколько метров ткани каждого типа потребуется для выполнения плана ?
2. Найти стоимость ткани, расходуемой на пошив изделия каждого вида.
3. Определить стоимость всей ткани, необходимой для выполнения плана.
4. Подсчитать стоимость всей ткани с учетом ее транспортировки.
Решение. Обозначим через А матрицу, данную нам в условии, т. е.,
A = ,
тогда для нахождения количества метров ткани, необходимой для выполнения плана, нужно вектор X умножить на матрицу А:
X А = (10,15, 23) = =
= (95, 40, 92, 129).
Стоимость ткани, расходуемой на пошив изделия каждого вида, найдем, перемножив матрицу А и вектор CT:
А CT = = .
Стоимость всей ткани, необходимой для выполнения плана, определится по формуле:
X А C T = (10,15,23) = .
= .
Наконец, с учетом транспортных расходов вся сумма будет равна стоимости ткани, т. е. 9472 ден. ед., плюс величина
X А P T = (95, 40, 92, 129) .
Итак, X А C T + X А P T = 9472 + 1037 = 10509 (ден. ед).







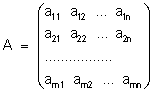


 .
. будет диагональной.
будет диагональной. 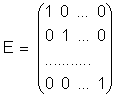 .
. .
.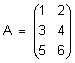 и
и  .
. и В =
и В =  .
. , а произведение BA не существует.
, а произведение BA не существует.









