Запись и реализация булевых функций в различных базисах
Понятие базиса
С помощью ограниченного набора элементарных функций можно представить любую, сколь угодно сложную функцию алгебры логики. Такой набор элементарных функций называют базисом или функционально полным набором.
Базис называют избыточным, если исключение одной элементарной функции не приводит к потере функциональной полноты. Иначе базис называют минимальным. Так, базисы 1,8 – избыточны, а остальные – минимальные.
Функциональная полнота.
Систему булевых функций называют функционально полной, если любая булева функция предст суперпозицией функций данной системы.
Теорема Поста. Система булевых функций функционально полна, если она не содерж целиком ни в одном из 5 замкнутых классов.
Замкнутые классы функций
1. Класс T0 функций, сохраняющих ноль 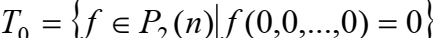
2. Класс T1 функций, сохраняющих ед 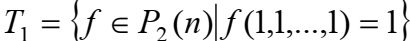
3. Класс S самодвойств функций сост функции, на противоп наборах приним противоп знач
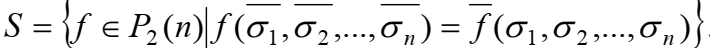
4. Класс М монотонных функций. Для двоичных векторов 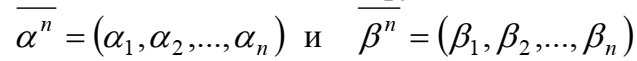 где
где 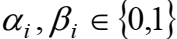 вводится следующее отношение частичного порядка. Считается, что
вводится следующее отношение частичного порядка. Считается, что 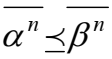 если
если 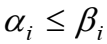 для
для 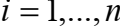
Класс M определяется следующим образом: 
Где 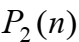 множество всех булевых функций n переменных
множество всех булевых функций n переменных
5. Класс линейных функций L составляют функции, которые представлены полиномом Жегалкина 1 степени.
Проверка принадлежности булевой функции замкнутым классам 1-4 делают по таблице истинности. Проверка принадлежности булевой функции классу L делают путем постррения полинома Жегалкина.
Для проверки функциональной полноты системы булевых функций строится т н таблица Поста, в которой отмечают принадлежность функций замкнутым классам. Если в каждом столбце таблицы Поста есть хотя бы один минус, система полна, в противном случае – нет.
Прим. Проверить функцио полноту системы булевых функций 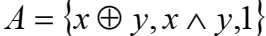
Проверим принадлежность замкнутым классам функции 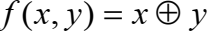 Построим табл истинности
Построим табл истинности
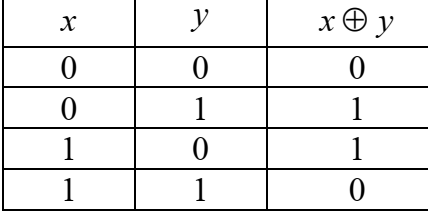 \
\
Ф предст полином Жегалкина 1 степени, следоват 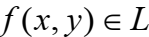
Рез0ты м занести в 1ю строку табл Поста. Остальные функции иссл анал
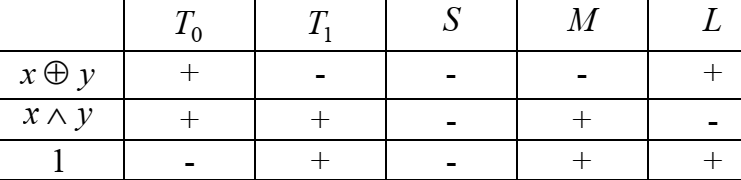
В каждом столбце табл имеется минус, след, система A функцион полна.
Мин функц полная система наз базисом пр-ва булевых функций.
Базисов может быть много:
1. И, ИЛИ, НЕ 2. И, НЕ
3. И – НЕ 4. НЕ – И
5. ИЛИ, НЕ 6. ИЛИ – НЕ
7. НЕ – ИЛИ 8. “0”, ”1”, НЕ,  n и другие.
n и другие.
Используя законы алгебры логики, можно переходить от одного базиса к другому.Например, пусть имеется элемент 3И-НЕ, а н реализ след оп:
НЕ . И (для 2-x перем) ИЛИ (для 2-x перем)
1)Операция НЕ получается на основании закона тавтологии (рис.1.16)
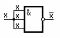 Рис 1.16 – Инвертор на элем Шеффера
Рис 1.16 – Инвертор на элем Шеффера
2. Операция И получается на основании законов тавтологии и двойного отрицания (рис. 1.17)
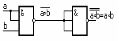 Рис1.17 – Конъюнктор на эл Шеффера
Рис1.17 – Конъюнктор на эл Шеффера
3. Операция ИЛИ получается на основании правила двойственности 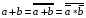 . Тогда получаем реализацию (рис. 1.18):
. Тогда получаем реализацию (рис. 1.18):
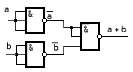 Рис 1.18 –Дизъюнктор на эл Шеффера
Рис 1.18 –Дизъюнктор на эл Шеффера
Базис (с-ть) эл-тов, выбранных для синтеза КС, всегда должен быть функциональго полным, т е допускать реализацию любой булевой функц на основе принципа суперпозиции.
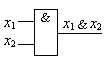
Если в качестве базиса выбр эл И, ИЛИ, НЕ, то счит что реализ булевый базис. Проектир схем в бул базисе наиб просто, так как все методы минимиз булевых функций в осн ориент на него. Поэтому, как п-ло, на 1 этапе КС проектир в булевом базисе с послед переходом в зад базис. Для удобства проектир возм реализация схем с исп смешанного базиса.
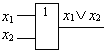
| Булевый базис – базис И, ИЛИ, НЕ | Базис И-НЕ (ш | Базис ИЛИ-НЕ |
| 
| 
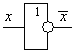
| 
| 
| 
|
Задача анализа зад КС свод к отыск булевой функ или смы булевых функ, опис работу этой КС с пом апп алгебры логики.
Задача синтеза КС сост в постр опт схемы проектир узла ува, исх из физич опис его работы (техн зад на проектиро).Зад синтеза схемы состоит в преобр логич ф в суперпоз логич эл зад типа. Исх булева функция д б предст в мин форме: МДНФ или МКНФ. На входах проектируемой схемы присутств перем как с отриц, так и без отрицания.
а) базис И, ИЛИ, НЕ (булевый базис).
Для постр сх на эл И, ИЛИ, НЕ м исп как МДНФ, так и МКНФ функции. В этом сл ф предст
в виде суперпоз опер логич эл И (коньюнкторов), оп логич эл ИЛИ (дизьюнкторов), инверторов.
б) базис И-НЕ.(базис Шеффера)
Для реализац исх булевой функции на эл И-НЕ необх от МДНФ функ взять двойное отрицание и одно из них раскр по п-лу Де Моргана, изб от дизьюнкции меж элем коньюнкциями.
 в базисе И, ИЛИ, Не.
в базисе И, ИЛИ, Не.
| Способы исп эл типа 2И-НЕ в качестве инвертора. | |

из получ аналит выр, лу д содер 3 двухвход и 1 трехвход эл И-НЕ. Функц схема комб ува, постр в базисе И-НЕ, пока на рис
в) базис ИЛИ-НЕ.базис Пирса или функция Вебба
Для реализ булевой функции на элементах ИЛИ-НЕ н от МКНФ функции взять двойное отрицание и одно из них раскрыть по правилу Де Моргана, избавившись от коньюнкции между элементарными дизьюнкциями.
| Способы исп эл типа 2ИЛИ-НЕ в качестве инвертора. | 
|
в) базис И-ИЛИ-НЕ.
Для реализации исх булевой ф на эл И-ИЛИ-НЕ необх от МКНФ ф взять дв отриц и одно из них раскр по п-лу Де Моргана:
Рассм ос-ти базисов И-Не и ИЛИ-Не. Элементы И-Не описываются функцией  .
.
Таблица истинности функции И-Не
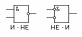
Если на оба входа эл И-Не подать одну и ту же переменную (1я и 4 строки таблицы), то в результате получим функцию:  , т. е. элемент И-Не стан инвертором (рис. 6.5, а). При последовательном соединении 2 элементов И-Не, как на рис. 6.5 (б), схема вып ф И. Таким обр, базис И-Не содержит как бы 3 эле – И-Не, И, Не.
, т. е. элемент И-Не стан инвертором (рис. 6.5, а). При последовательном соединении 2 элементов И-Не, как на рис. 6.5 (б), схема вып ф И. Таким обр, базис И-Не содержит как бы 3 эле – И-Не, И, Не.
Рис. 6.5. Соединение элементов базиса И-Не:
а – инвертор (Не); б – элемент И
Эл ИЛИ-Не описывает функцию  .
.
Таблица истин функции ИЛИ-Не
Если на оба входа эл ИЛИ-Не подать одну и ту же перем, то получ ф:  т. е. эл ИЛИ-Не стан инвертором (рис. 6.6, а). При послед соед двух эл ИЛИ-Не, как на рис. 6.6 (б), эл ИЛИ-Не преобр в эл ИЛИ. Таким обр, базис ИЛИ-Не содержит как бы 3 эл – ИЛИ-Не, ИЛИ, Не.
т. е. эл ИЛИ-Не стан инвертором (рис. 6.6, а). При послед соед двух эл ИЛИ-Не, как на рис. 6.6 (б), эл ИЛИ-Не преобр в эл ИЛИ. Таким обр, базис ИЛИ-Не содержит как бы 3 эл – ИЛИ-Не, ИЛИ, Не.
Соединение элементов базиса ИЛИ-Не:
а – инвертор (Не); б – элемент ИЛИ
Зад1. начертить схему реализ выраж  используя базис И-НЕ (базис Шеффера)
используя базис И-НЕ (базис Шеффера)
Зад2. Упростить функциональную схему –заменить на экв сост их эл И, ИЛИ,НЕ
 по з-ну двойств
по з-ну двойств
Отв
Зад 3 эквивалентны ли схемы
и
Н проверить экв ли ф-ии 
Схемы равносильны
Для предст логич функции в базисе Вебба в общем сл н:
исх лог ф предст в виде КНФ; в эл дизъюнк зн «+» замен на  и меж скобк пост
и меж скобк пост вмест «
вмест « »
»
Пример:
Логич ф в базисе Вебба м б записана с учет закона двойной инверсии или зна де Моргана
Если л ф д б запис только в базисе 2ИЛИ-НЕ, а кол лог перем у нее2, то н исп принцип суперпоз и преобр 1 и 2.
Напр:  , здесь
, здесь К получ выр примен преобр 1
К получ выр примен преобр 1


Подст запись для A в базисе Вебба в выр и получ:
и получ:
Логич базис ИЛИ-НЕ.Синтез логич схем по логич выражению в базисе ИЛИ-НЕ.
для постр логич у-ва любой сложности дост иметь однотипн логич эл напр, И-НЕ или ИЛИ-НЕ.
Реализ с пом логич функции ИЛИ-НЕ базовых функ алг Буля осущ след обр.
Для элемента "ИЛИ-НЕ"
| операция "НЕ" 
| операция "ИЛИ" 
| операция "И" 
|
Для элемента "И-НЕ"
| операция "НЕ" 
| операция "ИЛИ" 
| операция "И" 
|
Функция НЕ реализована с помощью схемы ИЛИ-НЕ с 1входом.
На рис. 2.8. приведена схемная реализация операции И, ИЛИ, НЕв базисе ИЛИ-НЕ
Базис {,,1 Полином Жегалкина
Полиномом Жегалкина называется представление логической функции в базисе {,,1}
В данном представлении инверсия реализуется как сумма по модулю 2 с константой 1.
Для представления ДНФ в виде полинома Жегалкина надо выразить дизъюнкцию через конъюнкцию и инверсию. Например:
хy= =(х1)(y1)1==xyxy11=xyxy. (11=0).
=(х1)(y1)1==xyxy11=xyxy. (11=0).
Пример. Представить в виде полинома Жегалкина логическую функцию xyz.
xyz= =(х1)(y1)(z1)1==(xyxy1)(z1)1=
=(х1)(y1)(z1)1==(xyxy1)(z1)1=
=xyzxzyzxyxy11==xyzxzyzxyxy.
Для преобразования полинома Жегалкина используются обычные приемы элементарной алгебры (исключение составляет равносильность аа=0).
Полином Жегалкина может быть получен по табл истинности путем суммирования по модулю два конъюнкций перем без инверсии xi и полиномов для инверсных перем (xj1) соотве рабочих наборов.Например, получим полином Жегалкина для функции f, таблица истинности которой имеет вид:
| x | y | z | f |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Тогда получим:
f=(x1)(y1)z(x1)y(z1)x(y1)(z1)xyz=
=(xyxy1)z(xzxz1)yx(yzyz1)xyz=
=xyzxzyzzxyzxyyzyxyzxyxzxxyz==xyz,
что и требовалось доказать, ибо и рассматривалась функция сложения по модулю 2 трех аргументов.
Реализация элемента “Равнозначность” (исключающее ИЛИ - НЕ)
Булево вырадение логической функции 
| в базисе И-НЕ | в базисе ИЛИ-НЕ |
| 
| 
|
Реализация элемента “Неравнозначность” (исключающее ИЛИ, сумма по модулю 2)
Булево выражение логической функции 
| в базисе И-НЕ | в базисе ИЛИ-НЕ |
| 
| 
|
Реализация элемента “Запрет”
На выходе такого элемента должна быть логическая 1, если на основном входе логическая единица, а на запрещающем входе – логический нуль.
Булево выражение логической функции элемента имеет вид  .
.
| в базисе И-НЕ | в базисе ИЛИ-НЕ |
| 
| 
|
ЛИТЕРАТУРА,ССЫЛКИ
1) С.Ф.Тюрин ,Лекции по дискретной математике, Лекция 6 ПНИПУ
https://studfiles.net/preview/476609/page:4/
2) В. Н. СЕМЕНЧУК ДИСКРЕТНАЯ МАТЕМАТИКА, Гомельский ГУ им. Франциска Скорины
3) Сергиевская И.М , Методические указания и контрольные задания по дискретной математике для студентов заочного ф-та, Поволжская ГА телекоммуникаций и информатики, Самара, 2002
4) НТУУ КПИ Лекции по архитектуре компьютера







 \
\

 n и другие.
n и другие.
 Рис 1.16 – Инвертор на элем Шеффера
Рис 1.16 – Инвертор на элем Шеффера Рис1.17 – Конъюнктор на эл Шеффера
Рис1.17 – Конъюнктор на эл Шеффера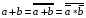 . Тогда получаем реализацию (рис. 1.18):
. Тогда получаем реализацию (рис. 1.18): Рис 1.18 –Дизъюнктор на эл Шеффера
Рис 1.18 –Дизъюнктор на эл Шеффера



















