Преобразование графических функций заданий ЕГЭ в рамках математического пространства

Преобразование графических функций заданий ЕГЭ в рамках математического пространства ( ЕГЭ профильный уровень. Задание 10 )

Пьявка О.А.

учитель математики,

МБОУ СОШУИП № 3,

г. Лабытнанги

В ЕГЭ 2021-2022 года в КИМ по математике профильного уровня было включено задание, связанное с преобразованием графиков функций. Для решения этой задачи нужно сначала определить формулу функции, а затем вычислить ответ на вопрос задачи. И если вычисление ответа по известной формуле обычно не составляет труда, определение самой формулы для данного графика функции часто ставит учащихся в тупик. Существует три разных подхода к решению данного вида заданий

• по целым координатам точек расположенных на графике функций (способ подходит вообще для любой задачи, но занимает достаточно много времени и требует хорошего навыка решения систем уравнений) преобразование графиков функций (способ сильно быстрее первого, но требует больше знаний, для использования преобразований функций нужно знать, как выглядят функции без изменения и как преобразования их меняют) комбинированный (идеально подходит для логарифмических и показательных функций, так как обычно у таких функций неизвестно основание и с помощью преобразований его не найти)
• по целым координатам точек расположенных на графике функций (способ подходит вообще для любой задачи, но занимает достаточно много времени и требует хорошего навыка решения систем уравнений)
• преобразование графиков функций (способ сильно быстрее первого, но требует больше знаний, для использования преобразований функций нужно знать, как выглядят функции без изменения и как преобразования их меняют)
• комбинированный (идеально подходит для логарифмических и показательных функций, так как обычно у таких функций неизвестно основание и с помощью преобразований его не найти)

Пример 1

На рисунке изображен график функции вида f(x)=ax 2 + bx+c , где числа a, b и c – целые. Найдите значение f(-2)

(4;6)

Пример 2

На рисунке изображен график функции вида f(x)=a х+| bx+c| +d , где числа

a, b, c и d – целые. Найдите корень уравнения ах + d=0

слева

справа

Решение

Решение

• На графике кусочно-линейная функция f(x)=a х+| bx+c| +d

• На графике кусочно-линейная функция f(x)=a х+| bx+c| +d

по определению раскроем модуль

у=ах +bx+c+d, если bx+c ≥ 0

по определению раскроем модуль

у=ах +bx+c+d, если bx+c ≥ 0

у = ах -bx- c+d, если bx+c ≤ 0

• у = ах -bx- c+d, если bx+c ≤ 0

у = ах -bx- c+d, если bx+c ≤ 0

• у = ах -bx- c+d, если bx+c ≤ 0

у= ( а +b)x+(c+d), если bx+c ≥ 0

у= ( а +b)x+(c+d), если bx+c ≥ 0

у =( а - b)x+( - c + d), если bx+c ≤0

Уравнение прямой имеет вид у= кх + l

C оотнесём коэффициенты после раскрытия модуля к(а± b) и l (± c+d)

2 . Определим прямые справа и слева и найдем вид каждой прямой

• у =( а - b)x+( - c + d), если bx+c ≤0 Уравнение прямой имеет вид у= кх + l C оотнесём коэффициенты после раскрытия модуля к(а± b) и l (± c+d) 2 . Определим прямые справа и слева и найдем вид каждой прямой

у =( а - b)x+( - c + d), если bx+c ≤0

Уравнение прямой имеет вид у= кх + l

C оотнесём коэффициенты после раскрытия модуля к(а± b) и l (± c+d)

2 . Определим прямые справа и слева и найдем вид каждой прямой

• у =( а - b)x+( - c + d), если bx+c ≤0 Уравнение прямой имеет вид у= кх + l C оотнесём коэффициенты после раскрытия модуля к(а± b) и l (± c+d) 2 . Определим прямые справа и слева и найдем вид каждой прямой

справа

слева

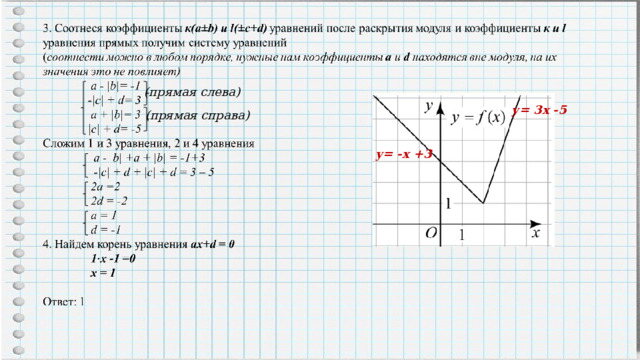
( прямая слева )

у= 3х -5

• у= 3х -5

( прямая справа )

у= -х +3

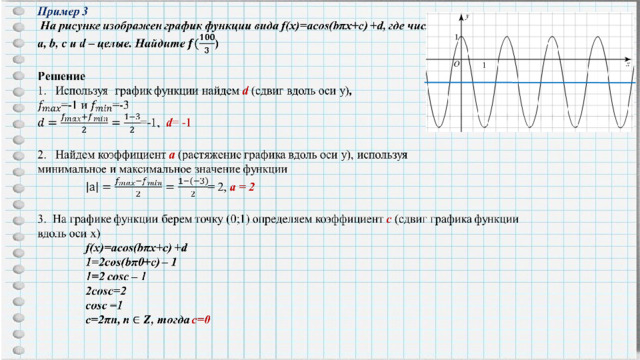
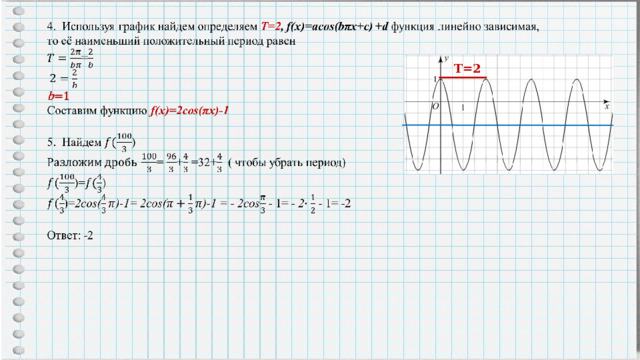
Т=2

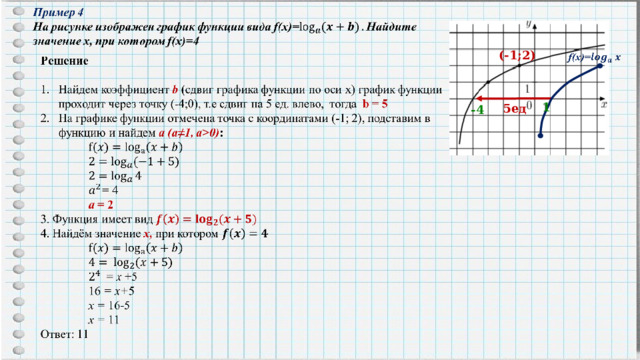
(-1;2)

1

5ед

-4

Решение

1. Найдём коэффициент b ( сдвиг графика функции по оси у)график функции проходит через точку (1;-3), т.е. сдвиг на 3ед. вниз, тогда b= - 3 .

( 4;-1)

(1 ;-3)

( -3;3)

( 0;2)

Пример 7

На рисунке изображен график функции вида f(x)=atgx +b. Найдите а .

(0 ; -1,5 )

(1;4)

(-3;1)

Спасибо за внимание!

Всем успехов в работе!