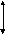Преобразование графиков элементарных функций в среде программирования visual basic

Ашинская районная научно-исследовательская конференция

научного общества учащихся

СОЗДАНИЕ ЦОР «ПРЕОБРАЗОВАНИЕ ГРАФИКОВ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ» В СРЕДЕ ПРОГРАММИРОВАНИЯ VISUAL BASIC

Автор: А. Чикишев, 9 класс

МОУ СОШ № 9, г. Аша

Научный руководитель: А. М. Гайфулин,

учитель математики

г. Аша

2009

Содержание

1. Введение…………………………………………………………….3

2. Основные понятия преобразования графиков……………………4

   1. Параллельный перенос………………………………………...4

   2. Изменение масштаба…………………………………………...7

3. Описание структуры проекта……………………………………...9

4. Программный код на языке Visual Basic………………………...11

5. Заключение………………………………………………………...13

6. Список литературы……………………………………………. . . 14

1. ВВЕДЕНИЕ

Цель проекта – создать программу, которая демонстрирует преобразование графиков элементарных функций. Интерактивность программы реализована с помощью текстовых полей, в которые можно вводить параметры преобразования.

Данная программа проста в применении и понятна для пользователя.

В процессе выполнения проекта были выполнены следующие задачи:

• Поиск информации и изучение теоретического материала по математике;

• Изучение основ программирования на языке Visual Basic;

• Освоение навыков работы в среде программирования Visual Basic;

• Анализ выполненной работы и перспективы её доработки.

Актуальность работы состоит в том, что на уроках алгебры можно применять компьютерные технологии без ущерба для математики, как предмета обучения т. к. проект имеет чисто практический, демонстрационный интерес. Его можно применять после завершения изучения теоретического материала или во время изучения для зрительного восприятия.

В данной работе используется способ визуализации информации. В ряде психологических исследований выявлено, что структурирование (установление взаимного расположения частей, составляющих целое) и схематизация (изображение или описание чего-либо в основных чертах) текстовой информации являются важнейшими компонентами процесса запоминания. Наглядно-образная форма представления информации способствует лучшему ее запоминанию.

Однако необходимо отметить, что наглядная форма представления учебной информации имеет недостаток. Любой схематизм способствует некоторой упрощенности понимания. Это может создать иллюзию, что для изучения определенного раздела вполне достаточно изображенного материала.

Наилучшие результаты в ходе обучения можно получить только при оптимальном сочетании различных способов представления информации: текстовой (логическое обоснование теории) и визуально-демонстрационной. Данный проект представляет собой не окончательный, а всего лишь один из возможных вариантов наглядного представления преобразования графиков.

Во всех имеющихся в наличии цифровых образовательных ресурсах по математике данная тема не обозначена чётко или участвует в виде заданий и упражнений, поэтому поставленная задача отличается новизной и оригинальностью решения.

2. ОСНОВНЫЕ ПОНЯТИЯ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ

2. 1. Параллельный перенос

Зависимости между переменными величинами описываются с помощью функций. Основные свойства этих функций не должны существенно меняться при изменении способа измерения переменных величин, т.е. при изменении их масштаба и начала отсчета. С другой стороны, за счет более рационального выбора способа измерения переменных величин обычно удается упростить запись зависимости между ними, привести эту запись к некоторому стандартному виду. На геометрическом языке изменение способа измерения величин означает некоторые простые преобразования графиков, к изучению которых мы и переходим.

Изменение начала отсчета переменных приводит к параллельному переносу. Возьмем переменную x и перенесем начало ее отсчета в точку x₀. Новую переменную обозначим через x^/. Связь между переменными x и x^/ записывается формулой x^/= x – x₀, или x= x^/ + x₀. Чтобы не ошибиться в знаке, полезно убедиться в том, что значению исходной переменной x = x₀ соответствует нулевое значение переменной x^/. Аналогично, сдвигая на y₀ значения переменной y, получим переменную y ^/, связанную с y формулой y ^/ =y – y₀, или y= y ^/ + y₀. Геометрически точки M (x; y), M^/ (x^/; y ^/) и M₀ (x₀; y₀) связаны векторным соотношением , или

.

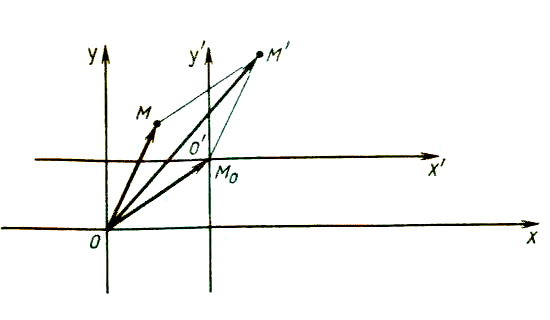
Рис. 1

Установим связь между графиками функций y = f (x) и y = f (x - a). Если мы обозначим x – a через x^/ (т. е. если мы сдвинем начало отсчета аргумента в точку a), то получим соотношение y = f (x^/). Это означает, что для построения графика функции y = f (x - a) надо изобразить график исходной функции в системе координат (x^/; y), т. е. сдвинуть график функции y = f (x) на вектор OM^/ (a; 0). Так как переменная y не меняется, то сдвиг происходит вдоль оси x (рис. 2).

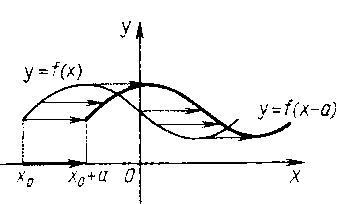Рис. 2

Этим же способом пользуются при сравнении графиков функций y = kx и y = kx + b.

Аналогично график функции y = f (x)+ b связан с графиком функции y = f (x). Обозначив y – b через y ^/, получим y^/ = f (x). Это означает, что для построения графика функции y = f (x)+ b надо изобразить график исходной функции f в системе координат (x; y ^/), т.е. сдвинуть график функции y = f (x) на вектор (0; b). При этом происходит параллельный перенос вдоль оси y (рис. 3).

Рис. 3

Иногда приходится менять начало отсчета одновременно и у аргумента x и y функции у, т. е. рассматривать зависимость вида y = f (x - a) + b (или y – b = f (x - a)). При построении графика функции y = f (x - a) + b надо сделать два параллельных переноса на векторы 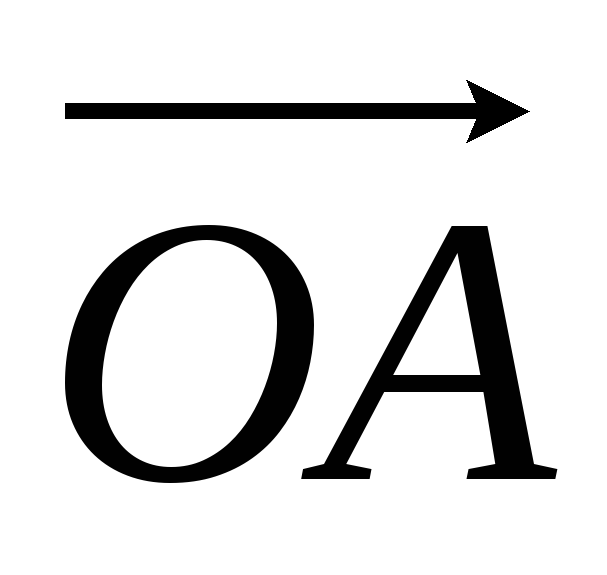и 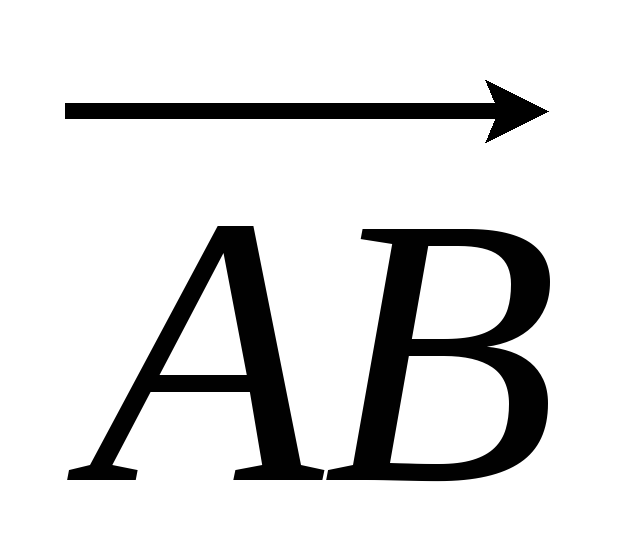, что можно заменить одним параллельным переносом на вектор 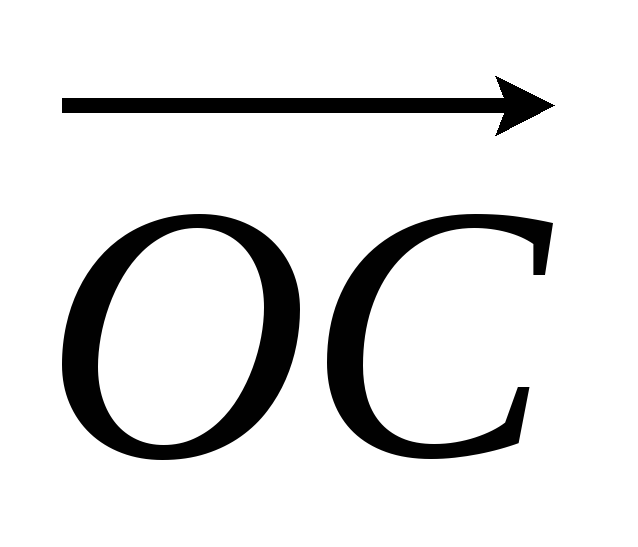(рис. 4). При этом точка (x₀; y₀) графика функции f (x) переходит в точку (x₀ + a; y₀ + b) графика функции y = f (x - a) + b.

Рис. 4

Различные примеры построения графиков с помощью параллельного переноса приведены на следующем рис.5.

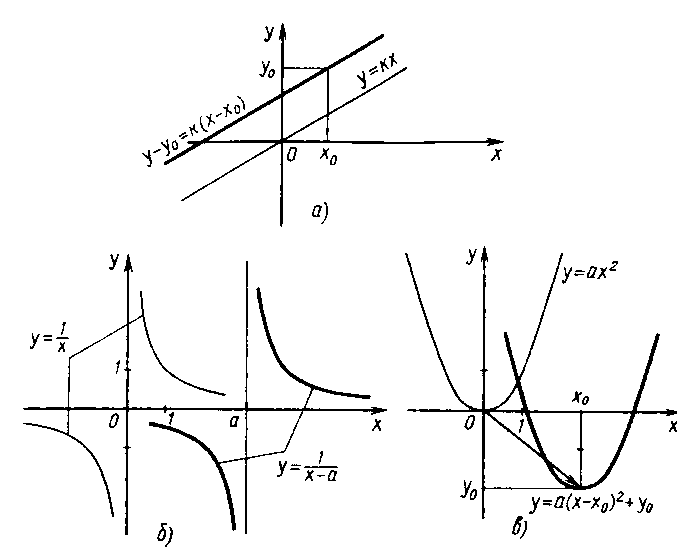
2. 2. Изменение масштаба

Изменим масштаб измерения величины x. Результат измерения в новом масштабе обозначим через x^/. Чтобы найти связь между значениями x и x^/, достаточно знать, какое значение переменной x^/ соответствует единице масштаба переменной x. Пусть это значение равно k. Тогда все другие значения переменной изменятся пропорционально, т. е. 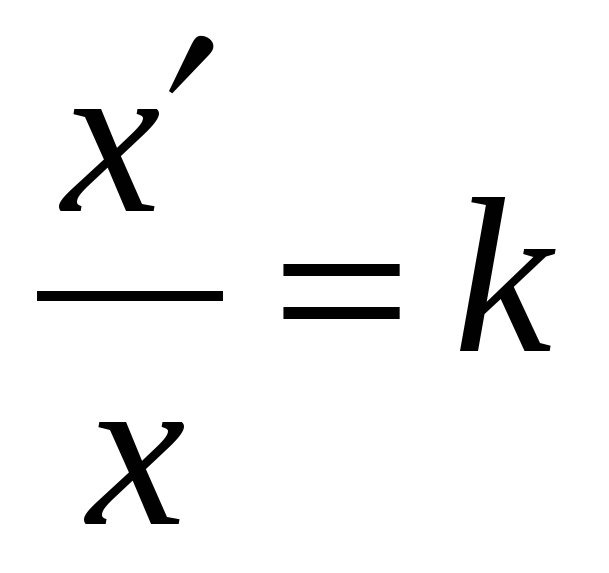, или x^/ = kx (проверим, что при x = 1 значение x^/ равно k).

Отсюда следует связь между графиками функций y = f (x) и y = f (kx) = =f (x^/), где x^/ = k x: график функции y = f (kx) получается из графика функции y = f (x) некоторым растяжением или сжатием вдоль оси x. При k 1 происходит сжатие графика, так как x^/ = 1 получается при 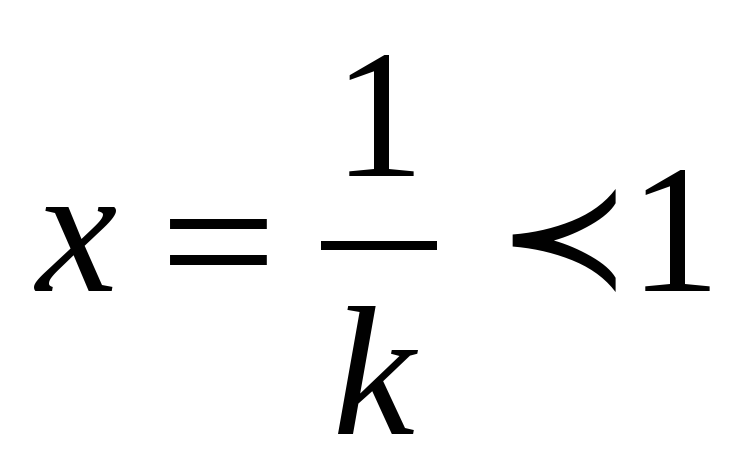и точка на исходном графике, соответствующая аргументу, равному 1, соответствует точке нового графика при 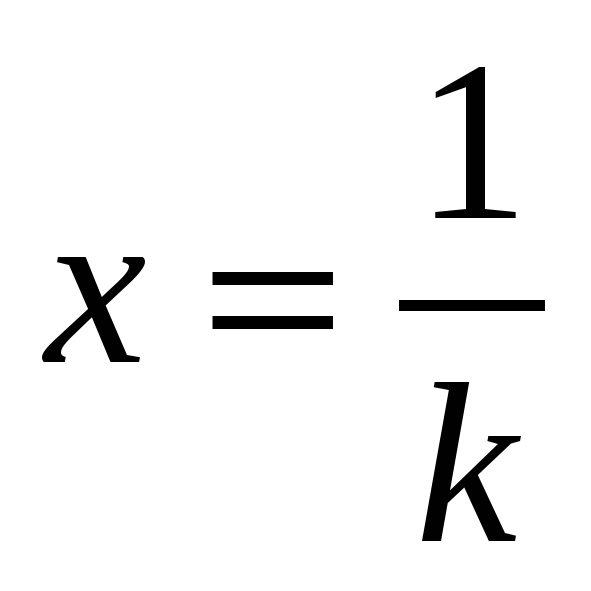. Аналогично при 0 k

Связь между графиками функций y = f (x) и y =kf (x) устанавливается аналогично. Только теперь надо менять масштаб измерения y:

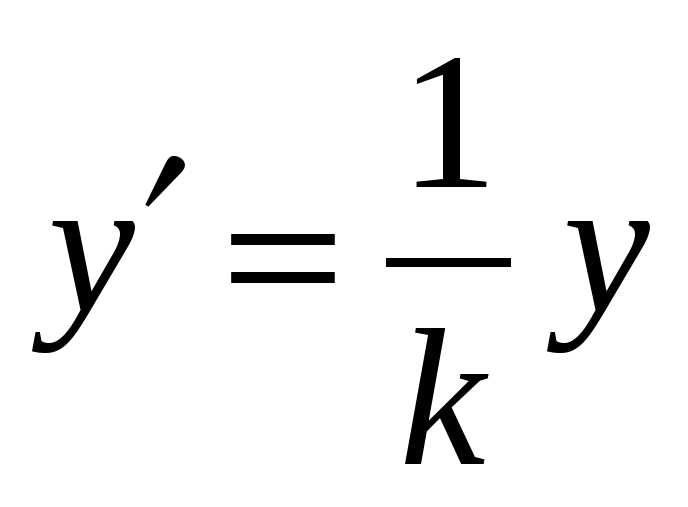, y =ky^’.

Ситуация стала противоположной – при k 1 происходит растяжение графика вдоль оси y, а при 0 k

Поведение графика при изменении масштаба изображено на рисунке 6.

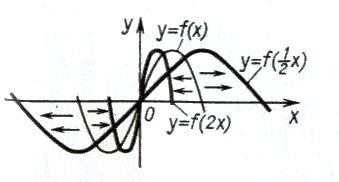Рис. 6

В преобразованиях y = f (kx) и y =kf (x) мы считали, что k 0. Чтобы включить и случай k k = - 1. Так как точки (x; y) и ( - x; y) симметричны относительно оси y, то и графики функций y = f (x) и y = - f (x) симметричны относительно оси x (рис. 7).

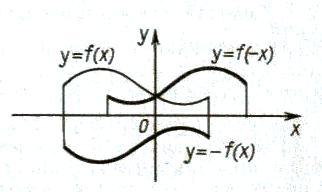
Пользуясь тремя типами преобразований графиков – параллельным переносом, растяжением (сжатием) и симметрией, можно, исходя из графика функции y = f (x), построить график функции y = Af (kx + b) + B при любых значениях параметров A, B, k, b.

3. ОПИСАНИЕ СТРУКТУРЫ ПРОЕКТА И ИНТЕРФЕЙС ПРОГРАММЫ

Проект состоит из восьми форм. Главная форма загружается первой при запуске проекта и соответственно становится видимой.

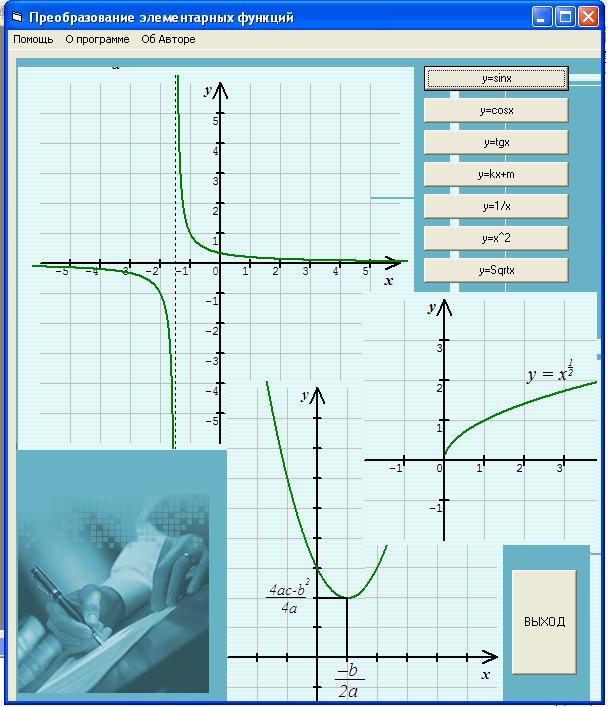
На ней расположены управляющие кнопки при помощи, которых организуются переходы на остальные семь форм. Так же предусмотрена кнопка с надписью ВЫХОД для завершения программы.

На других формах помещено графическое окно, в котором отображается график функции.

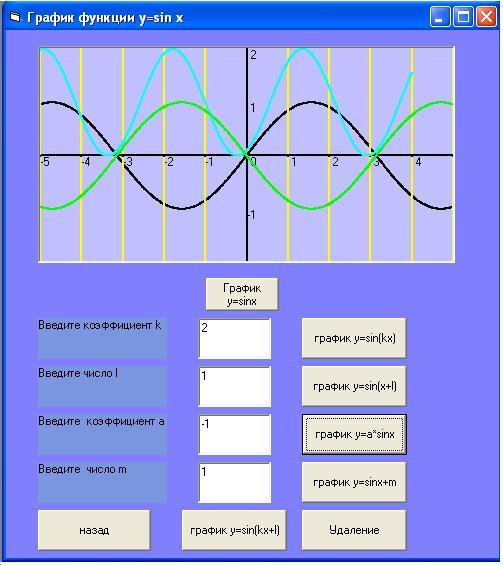
Внешне эти формы мало, чем отличаются, разве лишь количеством управляющих кнопок в зависимости от вида функции и типа преобразования. Для перехода на главную форму предусмотрена кнопка с надписью назад.

Схематически структура проекта имеет вид:

Главная форма

ПРОГРАММНЫЙ КОД НА ЯЗЫКЕ VISUAL BASIC

Dim sngX, intA, intB, intC, intD As Single, intI As Integer

Private Sub cmd1_Click()

picGraph.Scale (-5, 2)-(5, -2)

'Построение графика y=sinx

For sngX = -5 To 5 Step 0.01

picGraph.PSet (sngX, Sin(sngX))

Next sngX

'Координатная сетка

For intI = -5 To 5

picGraph.Line (intI, 2)-(intI, -2), vbYellow

Next intI 'Ось Х

picGraph.Line (-5, 0)-(5, 0)

For intI = -5 To 5

picGraph.PSet (intI, 0)

picGraph.Print intI

Next intI

picGraph.Line (0, 2)-(0, -2)

For intI = -2 To 2

picGraph.PSet (0, intI)

picGraph.Print intI

Next intI

End Sub

Private Sub Command1_Click()

intA = Val(Text1.Text)

For sngX = -5 To 5 Step 0.01

picGraph.PSet (sngX, Sin(intA * sngX)), vbRed

Next sngX

End Sub

Private Sub Command2_Click()

intB = Val(Text2.Text)

'Построение графика y=sin(x+l)

For sngX = -5 To 5 Step 0.01

picGraph.PSet (sngX - intB, Sin(sngX)), vbBlue

Next sngX

End Sub

Private Sub Command3_Click()

intC = Val(Text3.Text)

For sngX = -5 To 5 Step 0.01

picGraph.PSet (sngX, intC * Sin(sngX)), vbGreen

Next sngX

End Sub

Private Sub Command4_Click()

intD = Val(Text4.Text)

'Построение графика y=sinx+m

For sngX = -5 To 5 Step 0.01

picGraph.PSet (sngX, Sin(sngX) + intD), vbMagenta

Next sngX

End Sub

Private Sub Command5_Click()

intA = Val(Text1.Text)

intB = Val(Text2.Text)

intC = Val(Text3.Text)

intD = Val(Text4.Text)

'Построение графика y=a*sin(kx+l)+ m

For sngX = -5 To 5 Step 0.01

picGraph.PSet (sngX - intB, intC * Sin(intA * sngX) + intD), vbCyan

Next sngX

End Sub

Private Sub Command6_Click()

picGraph.Refresh

picGraph.Scale (-5, 2)-(5, -2)

'Построение графика y=sinx

For sngX = -5 To 5 Step 0.01

picGraph.PSet (sngX, Sin(sngX))

Next sngX

For intI = -5 To 5

picGraph.Line (intI, 2)-(intI, -2), vbYellow

Next intI 'Ось Х

picGraph.Line (-5, 0)-(5, 0)

For intI = -5 To 5

picGraph.PSet (intI, 0)

picGraph.Print intI

Next intI

picGraph.Line (0, 2)-(0, -2)

For intI = -2 To 2

picGraph.PSet (0, intI)

picGraph.Print intI

Next intI

End Sub

Private Sub Command7_Click()

Form1.Visible = True

frm11.Visible = False

End Sub

Private Sub Form_Load()

End Sub

5.ЗАКЛЮЧЕНИЕ

Опыт учителей позволяет заключить, что проект может быть методически использован на уроках математики по теме «Преобразование графиков» с применением проекционной аппаратуры и мультимедийных компьютерных технологий.

Работа имеет перспективу дальнейшего развития. В преобразовании графиков можно использовать эффекты анимации. Кроме того, проект можно дополнить теоретическим материалом, что позволит использовать его как ресурс в целях самообразования.

СПИСОК ЛИТЕРАТУРЫ

1. Алгебра и начала анализа 10-11 кл. Под ред. А. Н. Колмогорова, М. «Просвещение» 1994 г.

2. Алгебра и начала анализа 10-11 кл. М. И. Башмаков, М. «Просвещение» 1992 г.

3. Алгебра 8, Н.Я. Виленкин, А.Н. Виленкин, Г.С. Сурвилло и др.

4. Алгебра 9, Н.Я. Виленкин, Г.С. Сурвилло, А.С. Симонов, А.И.Кудрявцев.

5. Алгебра и математический анализ 10, Алгебра и математический анализ 11, авт. Н.Я. Виленкин, О.С. Ивашев-Мусатов, С.И. Шварцбурд.

6. И.Ф. Шарыгин, В.И. Голубев. Факультативный курс по математике (решение задач). Уч. пособие для 11 кл. М.: Просвещение, 1991г.

7. Черкасов Р.С., Столяр А.А. Методика преподавания математики в средней школе. М.: Просвещение, 1985г.

8. Информатика и информационные технологии 10-11 кл. Н. Д. Угринович М. БИНОМ. Лаборатория знаний 2005

9. Шмидт В. Microsoft Visual Basic 5.0. М, АБФ, 1997

10. Хальворсон М. Microsoft Visual Basic 5.0. М, ЭКОМ, 1988

14