Россия, Новый Уренгой
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 05.02.2022 14:06
Погорелова Наталья Михайловна
учитель математики
637
84 661 
Местоположение
Презентация для мастер класса "Решение логарифмических неравенств методом рационализации"
Категория:
Алгебра
02.02.2022 12:37
Просмотр содержимого документа
«Презентация для мастер класса "Решение логарифмических неравенств методом рационализации"»
Готовимся к ЕГЭ
Мастер-класс
Решение логарифмических неравенств методом рационализации
Погорелова Наталья Михайловна,
учитель математики первой квалификационной категории
МАОУ «СШ «Земля родная»
Метод рационализации неравенств известен около 50 лет, встречался под названиями: - метод декомпозиции; - метод замены множителей; - обобщение метода интервалов
Данный метод позволяет с помощью условий равносильности сводить решение целых классов сложных неравенств к решению простых рациональных неравенств классическим методом интервалов.
Идея метода рационализации состоит в использовании свойств монотонной функции.
Доказательства равносильных переходов приведены в пособии:
РЕШЕНИЕ НЕРАВЕНСТВ С ОДНОЙ
ПЕРЕМЕННОЙ
Прокофьев А.А., Корянов А.Г.
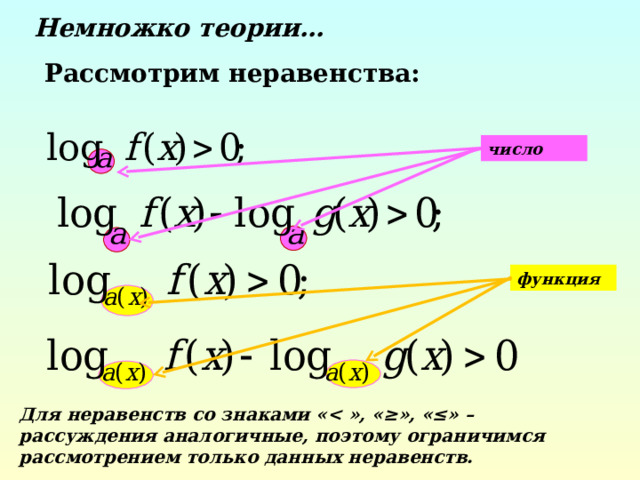
Немножко теории…
Рассмотрим неравенства:
число
функция
Для неравенств со знаками « », «≥», «≤» – рассуждения аналогичные, поэтому ограничимся рассмотрением только данных неравенств.
Знак «сохраняется».
Следовательно :
6
Знак «сохраняется».
Имеем :
7
При решении учитываем ограничения!
Решим неравенство:
-
+
+
x
- 1
x
x
7
Имеем:
7
Имеем:
7
Решим неравенство:
Ограничения:
7
-1
7
-
-
+
х
-1
3
х
-1
0
0, g 0, a 0, a 1) ( помните, что f 0, , a 0, a 1) ( помните, что f 0, a 0 , a 1) Примечание : a – функция от х или число, f и g – функции от х. " width="640"
На память…
Выражение (множитель) в неравенстве
(правая часть неравенства равна нулю!)
На что меняем
( помните, что f 0, g 0, a 0, a 1)
( помните, что f 0, , a 0, a 1)
( помните, что f 0, a 0 , a 1)
Примечание : a – функция от х или число, f и g – функции от х.
Решите неравенства:
Практикум
Ответы
к заданиям
- «Клик» по нужному заданию даёт переход к фрагменту решения и ответу
- Назад - в «Практимум»
-
+
+
+
-
x
-3
6
2
5
0
6
5
x
Для тех, кто боится «модулей» -
2 способ :
-
-
-
+
+
x
-3
6
2
5
D
0
6
5
x
0, g 0, a 0, a 1) ( помните, что f 0, , a 0, a 1) ( помните, что f 0, a 0 , a 1) Примечание : a – функция от х или число, f и g – функции от х. " width="640"
На память…
Выражение (множитель) в неравенстве
(правая часть неравенства равна нулю!)
На что меняем
( помните, что f 0, g 0, a 0, a 1)
( помните, что f 0, , a 0, a 1)
( помните, что f 0, a 0 , a 1)
Примечание : a – функция от х или число, f и g – функции от х.
В презентации использовались ресурсы:
1. Корянов А.Г., Прокофьев А.А. Интернет – ресурс: http://alexlarin.net/ege/20 20 /C3-20 20 .pdf
2. ЕГЭ. Математика. Профильный уровень: типовые экзаменационные варианты: 36 вариантов/ под ред.
И. В. Ященко –М. :Издательство «Национальное образование»,2020. -256с.-(ЕГЭ. ФИПИ- школе).
3. Экзаменационные задания: http : //alexlarin.net/
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
