Презентация "Факториал. Числа Фибоначчи" 10 класс ( углубленный уровень)

«Вычисление факториала. Числа Фибоначчи»

Болгова Н.А.

МБОУ СОШ с УИОП с.Тербуны

Тербунского муниципального района Липецкой области

Вспомним факториал:

N! = 1 * 2 * 3 * 4 * … * N

Факториал – произведение подряд идущих элементов числового ряда

Задание. Составьте функцию, которая вычисляет сумму элементов

Задача 1

Вход:

Выход

7

1.718

23

1.718

2 Этот прием называют рекурсией. " width="640"

Вспомним числа Фибоначчи:

1, 1, 2, 3, 5, 8, 13, 21, …

(Иногда ряд начинают с нуля: 0, 1, 1, 2, 3, 5, 8, ...

В данном случае мы будем придерживаться первого варианта)

Для вычисления Fn-го числа Фибоначчи необходимо знать( вычислить) два предыдущих и т.д.

Запишем в общем виде:

F1 = 1, F2 = 1

F3 = F2 + F1, Fn = F n-1 + F n-2, для n2

Этот прием называют рекурсией.

Задача. Вычислить 6-е число Фибоначчи

F6 = F5 + F4 # не знаем значений!

F5 = F4 + F3

F4 = F3 + F2

F3 = F2 + F1

Мы знаем, что первые два числа равны 1. Подставим значения начиная с F3 в обратном порядке.

F3 = 1 + 1 = 2

F4 = 2 + 1 = 3

F5 = 3 + 2 = 5

F6 = 5 + 3 = 8

Ответ: F6 = 8

Так работает рекурсия!

Представим рекурсию в виде дерева:

F6

F5

F4

F3

F4

F2

F3

F1

F2

F2

F3

F2

F1

F2

F1

6

Подставим значения:

8

F6

5

F4

F5

3

2

2

3

F2

F3

F4

F3

1

F1

F2

2

F2

F2

F1

F3

1

1

1

1

1

F1

F2

1

1

7

Пример программы:

def fib (n):

if n return 1 else : return fib(n - 1) + fib(n - 2)

print ( fib (int (input ( ) ) ) )

ВАЖНО помнить, что в Python числа начинаются с нулевого индекса. Поэтому для получения F6 необходимо ввести n=5

7

7

Задачи:

2. Дано число N. Напишите рекурсию, которая выводит все числа Фибоначчи до N включительно.

Вход:

Выход

10

1, 1, 2, 3, 5, 8

32

1,1,2, 3, 5, 8, 13, 21

Задачи:

3. Выведите двоичную запись числа N (без функции bin)

Вход:

Выход

4

100

15

1111

Вывод наоборот! Как исправить?

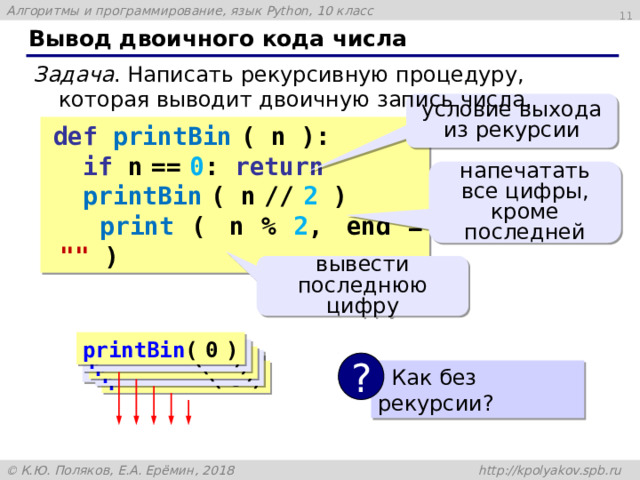
Вывод двоичного кода числа

Задача . Написать рекурсивную процедуру, которая выводит двоичную запись числа.

условие выхода из рекурсии

def printBin ( n ):

if n == 0 : return

printBin ( n // 2 )

print ( n % 2 , end = "" )

напечатать все цифры, кроме последней

вывести последнюю цифру

printBin ( 0 )

printBin ( 1 )

printBin ( 2 )

printBin ( 19 )

?

printBin ( 4 )

Как без рекурсии?

printBin ( 9 )

10011

11

11

Литература:

• Поляков К.Ю., Еремин Е.А. «Информатика 10 класс (базовый и углубленный уровни)»- Москва, Бином, 2018)
• informatics.mccme.ru
• Материалы Яндекс Лицея

11