Презентация "Формирование математической грамотности при подготовке к ОГЭ и ЭГЭ "

Формирование математической грамотности при подготовки к ОГЭ и ЕГЭ

Математическая грамотность – это способность человека мыслить математически, формулировать, применять и интерпретировать математику для решения задач в разнообразных практических контекстах.

Компоненты математической грамотности:

• воспроизведение математических фактов, методов и выполнение вычислений
• установление связей и интеграции материала из разных математических тем, необходимых для решения поставленной задачи
• математические размышления, требующие обобщения и интуиции

Поэтапное развитие различных умений, составляющих основу математической грамотности

Метапредметные результаты

УУД по формированию математической грамотности

5 класс

Уровень узнавания и понимания

находит и извлекает математическую информацию в различном контексте

6 класс

7 класс

применяет математические знания для решения разного рода проблем

Уровень понимания и применения

Уровень анализа и синтеза

формулирует математическую проблему на основе анализа ситуации

8 класс

Уровень оценки (рефлексии) в рамках предметного содержания

интерпретирует и оценивает математические данные в контексте лично значимой ситуации

9 класс

Уровень оценки (рефлексии) в рамках метапредметного содержания

интерпретирует и оценивает математические результаты в контексте национальной или глобальной ситуации

Что нужно уметь:

• Выделять ключевые фразы и основные вопросы из текста заданий.

• Уметь выполнять арифметические действия с различными числами, находить степень числа, извлекать арифметический квадратный корень из числа.

• Уметь переводить единицы измерения.

• Уметь округлять числа.

• Уметь находить число от процента и проценты от числа.

• Уметь находить часть от числа и число по его части.

• Применять основное свойство пропорции.

• Уметь решать уравнения, неравенства.

• Разбираться в изображениях рисунков, планов и масштабе фигур на рисунках.

• Анализировать и пользоваться информацией из таблиц.

• Анализировать и пользоваться заданными графиками.

Трудности в формировании математической грамотности:

• Мотивация.
• Отсутствие базовых знаний.
• Низкие способности.
• Не понимание прочитанного текста.
• Шаблонность мышления.
• Не способность рассуждать логически и убедительно формулировать аргументы .
• Не умение применять формулы и теоремы к решению задач.

Пути преодоления проблем

• Заинтересовать учащихся.
• Повышение вычислительных навыков.
• Повышение читательской грамотности.
• Проведение лабораторных и практических работ.
• Решение контекстных задач.
• Использование различных современных образовательных технологий.

Приёмы формирования математической грамотности.

• Технология критического мышления
• Технология проблемного обучения
• Проектная технология
• Игровая технология
• Информационно-коммуникационная технология
• Личностно-ориентированная технология

Учащиеся, овладевшие математической грамотностью, способны:

• распознавать проблемы, возникающие в окружающей действительности;
• формулировать проблемы на языке математики;
• решать, используя математические методы;
• анализировать использованные методы решения;
• интерпретировать полученные результаты;
• формулировать и записывать результаты решения проблемы.

Задания с элементами контекстных задач в ОГЭ

• Планировка квартиры.
• Листы бумаги.
• Маркировка шин.
• Печь для бани.
• План местности.
• Тарифы.
• Участок.
• Теплицы.
• Зонты.
• Кольцевая дорога.
• Оформление ОСАГО.
• Террасы.
• Зонт.

• Коробка.
• Колесо обозрения.
• Пицца
• Автозаправка
• Ремонт кухни
• Вертолётная площадка
• Метро
• Зоопарк

МАТЕМАТИЧЕСКАЯ ГРАМОТНОСТЬ. Пицца, 5 класс.

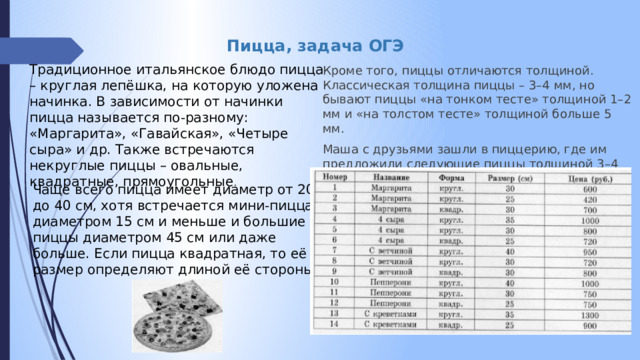
Пицца, задача ОГЭ

Традиционное итальянское блюдо пицца – круглая лепёшка, на которую уложена начинка. В зависимости от начинки пицца называется по-разному: «Маргарита», «Гавайская», «Четыре сыра» и др. Также встречаются некруглые пиццы – овальные, квадратные, прямоугольные .

Кроме того, пиццы отличаются толщиной. Классическая толщина пиццы – 3–4 мм, но бывают пиццы «на тонком тесте» толщиной 1–2 мм и «на толстом тесте» толщиной больше 5 мм.

Маша с друзьями зашли в пиццерию, где им предложили следующие пиццы толщиной 3–4 мм:

Чаще всего пицца имеет диаметр от 20 до 40 см, хотя встречается мини-пицца диаметром 15 см и меньше и большие пиццы диаметром 45 см или даже больше. Если пицца квадратная, то её размер определяют длиной её стороны.

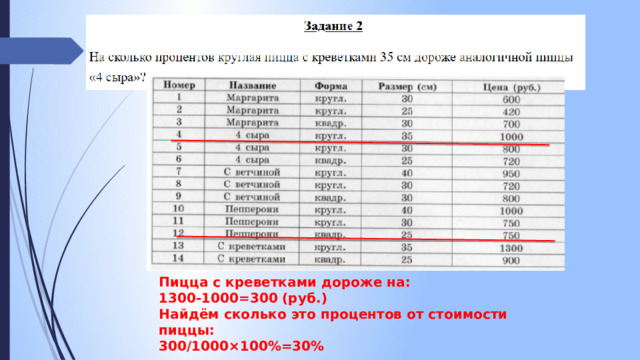
Пицца с креветками дороже на:

1300-1000=300 (руб.)

Найдём сколько это процентов от стоимости пиццы:

300/1000×100%=30%

Открытый банк заданий ЕГЭ и ОГЭ. Математика.

(34-2*10):2=7

МАТЕМАТИЧЕСКАЯ ГРАМОТНОСТЬ . Сберегательные вклады, 9 класс.

А) 1232:0,044=28000(руб.)

Б) 83000-28000=55000(руб.)-положили на второй счёт;

55000*0,07=3850(руб.)

28000

https://1.86143.3535.ru/14817/16341/

3850

Контекст: личный

Уровень сложности: средний

Задание ЕГЭ. Математика. Базовый уровень.

Через год клиент должен будет выплатить 12 000 + 0,13* 12 000  =  13 560 рублей.

Разделим 13 560 рублей на 12 месяцев.

Значит, клиент должен вносить ежемесячно в банк 1130 рублей. 

Ответ: 1130.

Математическая грамотность. Формат книги,8 класс.

84

60

8

16

Контекст: научный

Уровень сложности задания: средний

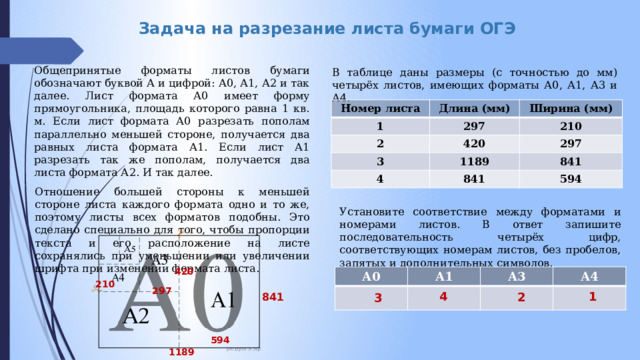
Задача на разрезание листа бумаги ОГЭ

Общепринятые форматы листов бумаги обозначают буквой А и цифрой: А0, А1, А2 и так далее. Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м. Если лист формата А0 разрезать пополам параллельно меньшей стороне, получается два равных листа формата А1. Если лист А1 разрезать так же пополам, получается два листа формата А2. И так далее.

Отношение большей стороны к меньшей стороне листа каждого формата одно и то же, поэтому листы всех форматов подобны. Это сделано специально для того, чтобы пропорции текста и его расположение на листе сохранялись при уменьшении или увеличении шрифта при изменении формата листа .

В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А0, А1, А3 и А4.

Номер листа

Длина (мм)

1

Ширина (мм)

297

2

420

3

210

1189

4

297

841

841

594

Установите соответствие между форматами и номерами листов. В ответ запишите последовательность четырёх цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.

420

А0

А1

А3

А4

210

297

4

1

2

841

3

594

1189

МАТЕМАТИЧЕСКАЯ ГРАМОТНОСТЬ .НАВЕС ДЛЯ АВТОМОБИЛЯ, 9класс

2

5

2

2

3

3

2,5

2,5

Уровень сложности: высокий

12 Уровень сложности:  высокий " width="640"

2

5

при заданных размерах тангенс угла наклона крыши равен 2/5, угол наклона равен 21 12

Уровень сложности:  высокий

Террасы, задача ОГЭ

Номер: 496A40. Открытый банк заданий ЕГЭ Математика. Базовый уровень.

L=(2,1+3,1)/2=2,6

МАТЕМАТИЧЕСКАЯ ГРАМОТНОСТЬ. Студенческая практика, 8 класс.

Свежие грибы содержат 100% − 90% = 10% питательного вещества, а высушенные — 100% − 12% = 88%.

0,1 · 250 = 25 кг питательного вещества в свежих грибах.

25:0,88≈28 кг сушеных грибов, получится из свежих грибов.

28

Уровень сложности: высокий

Номер: 1DA741. Открытый банк заданий ЕГЭ Математика. Базовый уровень.

70

30

20

Ответ:530

Номер: A6034F. Открытый банк заданий ЕГЭ Математика. Базовый уровень.

Номер: F39F45. Открытый банк заданий ЕГЭ Математика. Базовый уровень.

Ответ:145

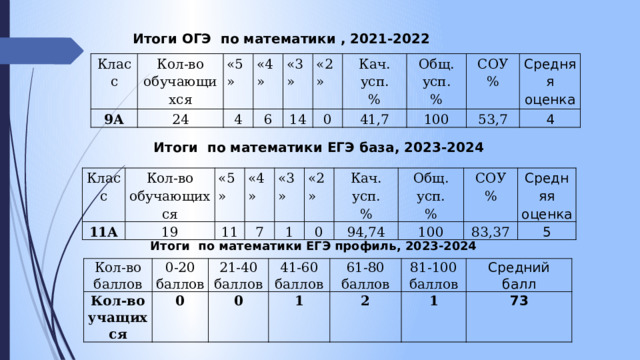
Итоги ОГЭ по математики , 2021-2022

Класс

9А

Кол-во обучающихся

«5»

24

4

«4»

«3»

6

14

«2»

0

Кач. усп.

41,7

Общ. усп.

%

СОУ

%

100

%

Средняя оценка

53,7

4

Итоги по математики ЕГЭ база, 2023-2024

Класс

11А

Кол-во обучающихся

«5»

19

11

«4»

«3»

7

1

«2»

Кач. усп.

0

94,74

Общ. усп.

%

100

СОУ

%

83,37

Средняя оценка

%

5

Итоги по математики ЕГЭ профиль, 2023-2024

Кол-во

Кол-во

0-20 баллов

баллов

0

учащихся

21-40 баллов

0

41-60 баллов

1

61-80 баллов

2

81-100 баллов

1

Средний балл

73

Развивать математическую грамотность надо постепенно, начиная с 5 класса. Регулярно включать в ход урока задания на «изменение и зависимости», «пространство и форма», «неопределенность», «количественные рассуждения» и т.п..

Эти задания можно использовать по усмотрению учителя:

• Как игровой момент на уроке;
• Как проблемный элемент в начале урока;
• Как задание – «толчок» к созданию гипотезы для исследовательского проекта;
• Как задание для смены деятельности на уроке;
• Как модель реальной жизненной ситуации, иллюстрирующей необходимость изучения какого либо понятия на уроке;
• Как задание, устанавливающее межпредметные связи в процессе обучения;
• Некоторые задания заставят сформулировать свою точку зрения и найти аргументы для её защиты;
• Можно собрать задания одного типа и провести урок в соответствии с какой то образовательной технологией;
• Задания такого типа можно включать в школьные олимпиады, математические викторины.

https://fg.resh.edu.ru/

https://uchi.ru/lp/funcgram

https://rikc.by/ru/PISA/2-ex__pisa.pdf

https://iro23.ru/?page_id=3076

Вывод, математическая грамотность становится фактором, содействующим развитию способностей учащихся творчески мыслить и находить нестандартные решения, умений выбирать профессиональный путь, использовать информационно-коммуникационные технологии в различных сферах жизнедеятельности, а также обучению на протяжении всей жизни.