Презентация. Функции

ФУНКЦИИ

0 у = кх, к 0 Прямой пропорциональностью называется функция, которую можно записать формулой вида у=кх, где х – независимая переменная, к – некоторое число. Графиком прямой пропорциональности является прямая линия, проходящая через начало координат у х 0 " width="640"

Прямая пропорциональность

у = кх, к 0

у = кх, к 0

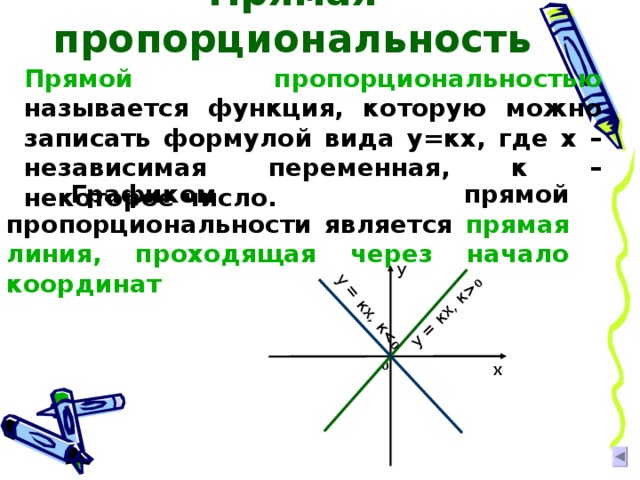
Прямой пропорциональностью называется функция, которую можно записать формулой вида у=кх, где х – независимая переменная, к – некоторое число.

Графиком прямой пропорциональности является прямая линия, проходящая через начало координат

у

х

0

Линейная функция

у = кх + b

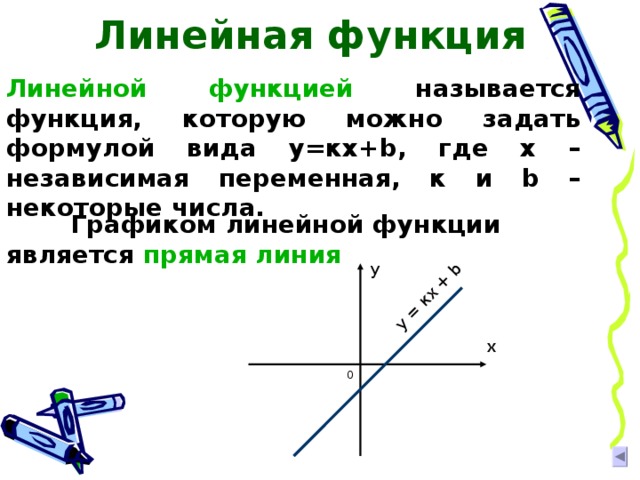
Линейной функцией называется функция, которую можно задать формулой вида у=кх+ b , где х – независимая переменная, к и b – некоторые числа.

Графиком линейной функции является прямая линия

у

х

0

Взаимное расположение графиков линейных функций у=к 1 х + b 1 и у=к 2 х + b 2

у=к 1 х+ b 1

у=к 2 х+ b 2

у=к 1 х+ b 1

у=к 2 х+ b 2

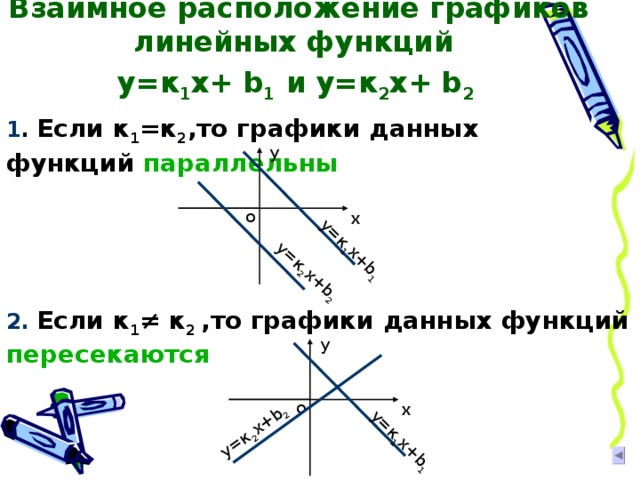
1 . Если к 1 =к 2 ,то графики данных функций параллельны

у

о

х

2. Если к 1 ≠ к 2 ,то графики данных функций пересекаются

у

о

х

0. Противоположным значениям х соответствует одно и тоже значение у " width="640"

у = х 2

Функция у = х 2

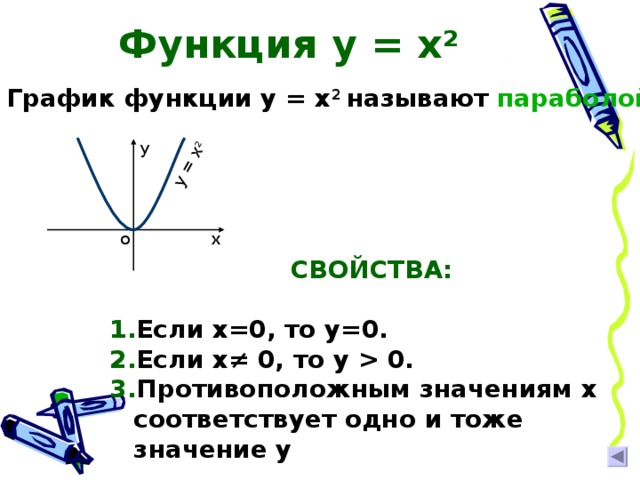
График функции у = х 2 называют параболой

у

о

х

СВОЙСТВА:

• Если х=0, то у=0.
• Если х≠ 0, то у 0.
• Противоположным значениям х соответствует одно и тоже значение у

0, то у 0 и если х 0, то у 0. Противоположным значениям х соответствуют противоположные значения у " width="640"

у = х 3

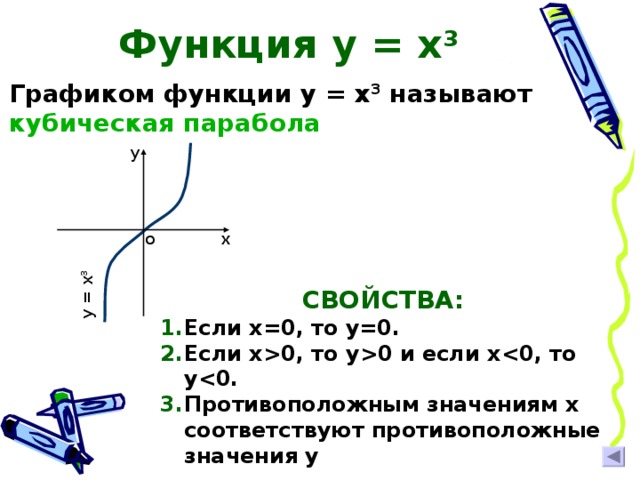
Функция у = х 3

Графиком функции у = х 3 называют кубическая парабола

у

х

о

СВОЙСТВА:

• Если х=0, то у=0.
• Если х 0, то у 0 и если х 0, то у 0.
• Противоположным значениям х соответствуют противоположные значения у

о , к о х " width="640"

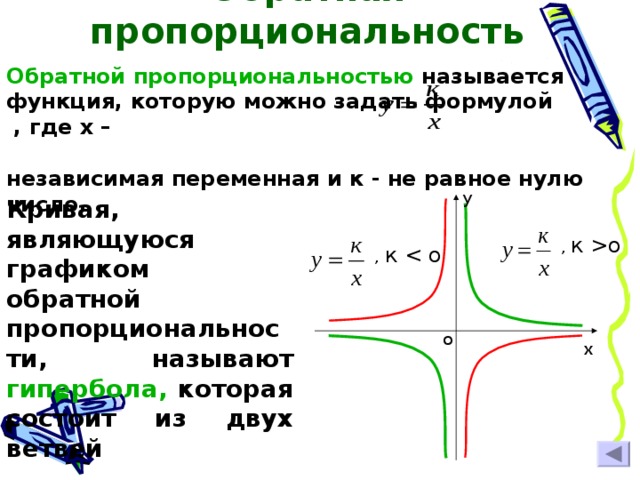
Обратная пропорциональность

Обратной пропорциональностью называется функция, которую можно задать формулой , где х –

независимая переменная и к - не равное нулю число.

у

Кривая, являющуюся графиком обратной пропорциональности, называют гипербола, которая состоит из двух ветвей

, к о

, к

о

х

0, то у 0 Большему значению аргумента соответствует большее значение функции " width="640"

У=√х

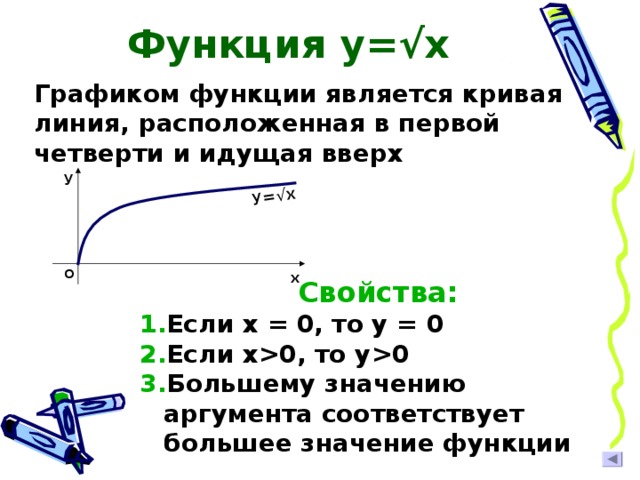
Функция у=√х

Графиком функции является кривая линия, расположенная в первой четверти и идущая вверх

у

о

х

Свойства:

• Если х = 0, то у = 0
• Если х 0, то у 0
• Большему значению аргумента соответствует большее значение функции

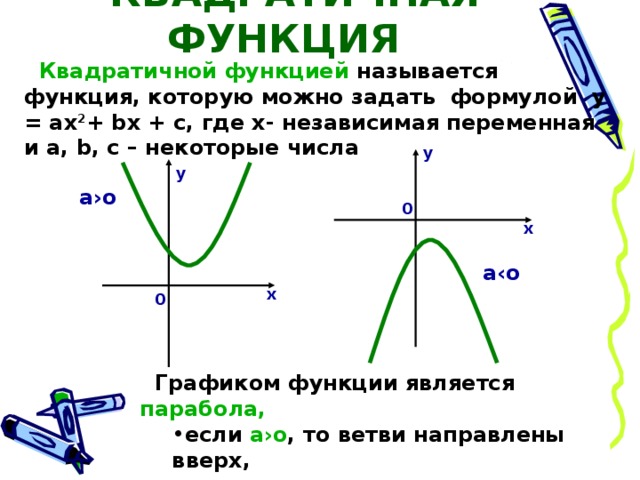
КВАДРАТИЧНАЯ ФУНКЦИЯ

Квадратичной функцией называется функция, которую можно задать формулой у = ах 2 + b х + с, где х- независимая переменная и a, b , с – некоторые числа

у

у

а›о

0

х

а‹о

х

0

Графиком функции является парабола,

• если а›о , то ветви направлены вверх, если а‹о , то ветви направлены вниз
• если а›о , то ветви направлены вверх,
• если а‹о , то ветви направлены вниз