Презентация «Готовимся к ОГЭ по информатике. Задание 3»

ОГЭ по информатике

Часть 1. Задание 3

Справочная информация

Алгебра логики – раздел математики, объектами которого являются высказывания.

Высказывание – это повествовательное предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное. В русском языке высказывания выражаются повествовательными предложениями.

Простое высказывание может быть либо истинно , либо ложно . Несколько простых высказываний, объединенных с помощью логических связок, называются составными высказываниями .

Простые высказывания обозначаются именами логических переменных , которые могут принимать значения логических констант : 1 (« истина ») и 0 (« ложь ») .

A = «2 × 2 = 4» (A = 1)

B = «2 × 2 = 5» (B = 0)

Над простыми высказываниями можно производить логические операции , в результате которых получаются составные высказывания.

Основные логические операции : конъюнкция, дизъюнкция, инверсия.

Справочная информация

1. Конъюнкция (логическое умножение) – объединение двух высказываний в одно с помощью союза « И ». Полученное составное высказывание будет истинным тогда и только тогда, когда истинны оба входящих в него простых высказывания.

«2 × 2 = 4» и «3 × 3 = 10» – ложь

«2 × 2 = 4» и «3 × 3 = 9» – истина

На формальном языке алгебры логики конъюнкция обозначается знаком « & ».

Например: A & B (читается «A и B»).

Значение логической операции определяется с помощью таблицы истинности , которая показывает, какие значения принимает результат логической операции при всех возможных наборах значений исходных высказываний (в следующем порядке: 00, 01, 10, 11).

Таблица истинности:

A

0

B

A & B

0

0

0

1

1

1

0

0

0

1

1

Справочная информация

2. Дизъюнкция (логическое сложение) – объединение нескольких высказываний с помощью союза « ИЛИ ». Полученное составное высказывание будет истинным тогда, когда истинно хотя бы одно из входящих в него простых высказываний.

«2 × 2 = 5» или «3 × 3 = 10» – ложь

«2 × 2 = 5» или «3 × 3 = 9» – истина

На формальном языке алгебры логики дизъюнкция обозначается знаком « v ».

Например: A v B (читается «A или B»).

Таблица истинности:

A

0

B

A v B

0

0

0

1

1

1

1

0

1

1

1

Справочная информация

3. Инверсия (логическое отрицание) – присоединение частицы « НЕ » к высказыванию. Инверсия делает истинное высказывание ложным, а ложное – истинным.

«2 × 2 = 4» – истина

«2 × 2 ≠ 4» – ложь.

На формальном языке алгебры логики инверсия обозначается (иногда ¬ A ).

Например: (читается «не A»).

Таблица истинности:

A

A

0

0

1

1

1

1

0

0

Порядок выполнения логических операций:

• операции в скобках;
• инверсия (НЕ);
• конъюнкция (И);
• дизъюнкция (ИЛИ).

3-1

Для какого числа x истинно высказывание:

( x И НЕ ( x

Решение.

Сначала избавимся от операции отрицания, заменив высказывание противоположным ему:

НЕ ( x x ≥ 4 ( x НЕ меньше 4, значит x либо больше 4, либо равен 4).

Составное высказывание примет вид:

( x И ( x ≥ 4).

Результат операции И (конъюнкции) будет истинным только тогда, когда истинны оба простых высказывания.

Этому соответствует число 4. На числовой оси это выглядит так:

5

4

6

7

Ответ: 4.

Обращайте внимание на дополнительные требования к ответу: это может быть наибольшее или наименьшее число, двузначное или трёхзначное, возможно потребуется записать количество подходящих чисел.

16) И НЕ ( x нечётное). Решение. Сначала избавимся от операции отрицания, заменив высказывание противоположным ему: НЕ ( x нечётное)  ( x чётное). Составное высказывание примет вид: ( x 16) И ( x чётное). Результат операции И (конъюнкции) будет истинным только тогда, когда истинны оба простых высказывания. Этому соответствует наименьшее чётное число, которое больше 16, то есть число 18. На числовой оси это выглядит так:       17 16 18 19 Ответ: 18. " width="640"

3-2

Напишите наименьшее число x, для которого истинно высказывание:

( x 16) И НЕ ( x нечётное).

Решение.

Сначала избавимся от операции отрицания, заменив высказывание противоположным ему:

НЕ ( x нечётное)  ( x чётное).

Составное высказывание примет вид:

( x 16) И ( x чётное).

Результат операции И (конъюнкции) будет истинным только тогда, когда истинны оба простых высказывания.

Этому соответствует наименьшее чётное число, которое больше 16, то есть число 18.

На числовой оси это выглядит так:

17

16

18

19

Ответ: 18.

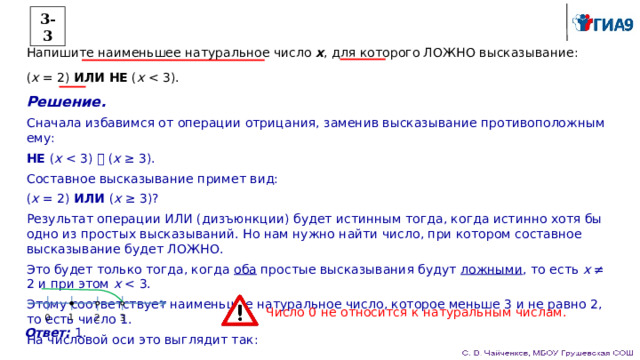
3-3

Напишите наименьшее натуральное число x , для которого ЛОЖНО высказывание:

( x = 2) ИЛИ НЕ ( x

Решение.

Сначала избавимся от операции отрицания, заменив высказывание противоположным ему:

НЕ ( x x ≥ 3).

Составное высказывание примет вид:

( x = 2) ИЛИ ( x ≥ 3)?

Результат операции ИЛИ (дизъюнкции) будет истинным тогда, когда истинно хотя бы одно из простых высказываний. Но нам нужно найти число, при котором составное высказывание будет ЛОЖНО.

Это будет только тогда, когда оба простые высказывания будут ложными , то есть x ≠ 2 и при этом x

Этому соответствует наименьшее натуральное число, которое меньше 3 и не равно 2, то есть число 1.

На числовой оси это выглядит так:

Число 0 не относится к натуральным числам.

1

0

2

3

Ответ: 1.

2)) И ( x 0)? Решение. Составное высказывание содержит 4 простых высказывания и 3 логических операции. Расставим порядок выполнения в соответствии с приоритетом операций. 2 1 3 ( x И (( x ИЛИ ( x 2)) И ( x 0)? Результат операции ( x ИЛИ ( x 2) будет истинным тогда, когда истинно хотя бы одно из двух простых высказываний, т. е. x ≠ 2. Чтобы всё высказывание с операцией И было истинным, должны быть истинными каждое из входящих в него высказываний, т. е. ( x И ( x ≠ 2) И ( x 0) . На числовой оси это выглядит так:             1 0 2 3 Ответ: 1. " width="640"

3-4

Для какого числа x истинно высказывание:

( x И (( x ИЛИ ( x 2)) И ( x 0)?

Решение.

Составное высказывание содержит 4 простых высказывания и 3 логических операции. Расставим порядок выполнения в соответствии с приоритетом операций.

2 1 3 ( x И (( x ИЛИ ( x 2)) И ( x 0)?

Результат операции ( x ИЛИ ( x 2) будет истинным тогда, когда истинно хотя бы одно из двух простых высказываний, т. е. x ≠ 2.

Чтобы всё высказывание с операцией И было истинным, должны быть истинными каждое из входящих в него высказываний, т. е. ( x И ( x ≠ 2) И ( x 0) .

На числовой оси это выглядит так:

1

0

2

3

Ответ: 1.

3-5

Напишите наименьшее трёхзначное число, для которого истинно высказывание:

НЕ (Первая цифра нечётная) И (число делится на 3)?

Решение.

Избавимся от операции отрицания, заменив высказывание противоположным ему:

НЕ (Первая цифра нечётная)  (Первая цифра чётная).

Составное высказывание примет вид:

(Первая цифра чётная) И (число делится на 3).

Результат операции И будет истинным только тогда, когда истинны оба простых высказывания.

Так как число должно быть наименьшим трёхзначным с первой чётной цифрой , то число будет минимум 200. Но оно не делится на 3. Ближайшим к нему числом, делящимся на 3, будет число 201 (201 / 3 = 67).

Ответ: 201.

12). Решение. Избавимся от операций отрицания, заменив высказывание противоположным ему: НЕ (Число нечётное)  (Число чётное) НЕ (Число 12)  (Число ≤ 12) Составное высказывание примет вид: (Число чётное) И (Число ≤ 12). Результат операции И будет истинным только тогда, когда истинны оба простых высказывания. Этому соответствуют натуральные чётные числа 2, 4, 6, 8, 10, 12. Их количество равно 6. Ответ: 6. " width="640"

3-6

Напишите количество натуральных чисел, для которых истинно высказывание:

НЕ (Число нечётное) И НЕ (Число 12).

Решение.

Избавимся от операций отрицания, заменив высказывание противоположным ему:

НЕ (Число нечётное)  (Число чётное)

НЕ (Число 12)  (Число ≤ 12)

Составное высказывание примет вид:

(Число чётное) И (Число ≤ 12).

Результат операции И будет истинным только тогда, когда истинны оба простых высказывания.

Этому соответствуют натуральные чётные числа 2, 4, 6, 8, 10, 12. Их количество равно 6.

Ответ: 6.

60) ИЛИ ( х чётное) ). Чтобы всё высказывание было истинным , результат операции ИЛИ в скобках должен быть ложным . То есть х ≤ 60 и нечётное, при этом оно должно быть наибольшим возможным. Этому соответствует число 59. Ответ: 59. " width="640"

3-7

Напишите наибольшее число x , для которого истинно высказывание:

НЕ (НЕ ( х ИЛИ ( х чётное) ) .

Решение.

Расставим порядок выполнения в соответствии с приоритетом операций.

3 1 2 НЕ (НЕ ( х ИЛИ ( х чётное) ).

Избавимся от первой операции отрицания:

НЕ ( ( х 60) ИЛИ ( х чётное) ).

Чтобы всё высказывание было истинным , результат операции ИЛИ в скобках должен быть ложным .

То есть х ≤ 60 и нечётное, при этом оно должно быть наибольшим возможным. Этому соответствует число 59.

Ответ: 59.