Презентация «Готовимся к ОГЭ по информатике. Задание 5»

ОГЭ по информатике

Часть 1. Задание 5

Справочная информация

Исполнитель – это некоторый объект (человек, животное, техническое устройство), способный выполнять определённый набор команд.

Система команд исполнителя (СКИ) – набор команд, которые понимает и может выполнять конкретный исполнитель.

Алгоритм – понятное и точное предписание некоторому исполнителю совершить последовательность действий, обеспечивающую получение требуемого результата из исходных данных.

Неформальный исполнитель ( например – человек) одни и те же команды может выполнять по-разному.

Формальный исполнитель ( например – компьютер, робот, техническое устройство) всегда одинаково выполняет одну и ту же команду. От него не требуется понимание сущности решаемой задачи, за его действия отвечает управляющий им объект (составитель алгоритма).

Справочная информация

Свойства алгоритмов:

• Дискретность – алгоритм разбивается на последовательность отдельных шагов (команд), следующих в определённом порядке.
• Понятность – алгоритм должен содержать только те команды, которые входят в систему команд исполнителя.
• Определённость – каждая команда должна строго и однозначно определять действие исполнителя.
• Результативность – исполнение алгоритма должно завершиться за конечное число шагов и привести к получению результата.
• Массовость – желательно, чтобы алгоритм обеспечивал решение некоторого класса однотипных задач при различных исходных данных.

В этом задании требуются навыки исполнения или создания линейных алгоритмов для формального исполнителя с фиксированным набором команд.

Потребуются также навыки решения линейных или квадратных уравнений.

5-1

У исполнителя Вычислитель две команды, которым присвоены номера:

1. раздели на 2

2. вычти 1

Первая из них уменьшает число на экране в 2 раза, вторая уменьшает его на 1.

Исполнитель работает только с натуральными числами.

Составьте алгоритм получения из числа 65 числа 4 , содержащий не более 5 команд.

В ответе запишите только номера команд. Если таких алгоритмов более одного, то запишите любой из них.

Решение.

Исходное число 65. К нему нельзя применить команду «раздели на 2» , поэтому выполним команду «вычти 1» .

Получим число 64, к нему можно применить команду «раздели на 2» .

Рассуждая аналогично, запишем команды алгоритма получения из числа 65 числа 4.

2. вычти 1 65 – 1 = 64

1. раздели на 2 64 : 2 = 32

1. раздели на 2 32 : 2 = 16

1. раздели на 2 16 : 2 = 8

1. раздели на 2 8 : 2 = 4

Запишем алгоритм из номеров команд: 21111.

Ответ: 21111.

5-2

У исполнителя Вычислитель две команды, которым присвоены номера:

1. возведи в квадрат

2. прибавь 1

Первая из них возводит число на экране во вторую степень, вторая – прибавляет к числу 1.

Составьте алгоритм получения из числа 2 числа 37 , содержащий не более 5 команд.

В ответе запишите только номера команд. Если таких алгоритмов более одного, то запишите любой из них.

Решение.

В данном случае к исходному числу можно применить любую из двух команд. В этой ситуации можно воспользоваться методом решения обратной задачи.

То есть мы будем получать из числа 37 число 2 , используя команды, обратные исходным:

1. извлеки квадратный корень

2. вычти 1

2. вычти 1 37 – 1 = 36

1. извлеки квадратный корень = 6

2. вычти 1 6 – 1 = 5

Полученный алгоритм надо будет записать из номеров команд в обратном порядке: 12212.

2. вычти 1 5 – 1 = 4

1. извлеки квадратный корень = 2

Ответ: 12212.

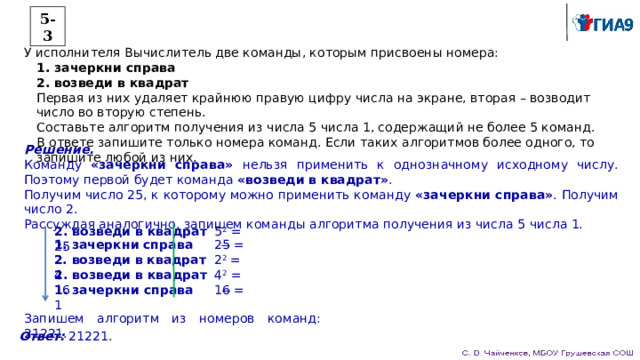
5-3

У исполнителя Вычислитель две команды, которым присвоены номера:

1. зачеркни справа

2. возведи в квадрат

Первая из них удаляет крайнюю правую цифру числа на экране, вторая – возводит число во вторую степень.

Составьте алгоритм получения из числа 5 числа 1, содержащий не более 5 команд.

В ответе запишите только номера команд. Если таких алгоритмов более одного, то запишите любой из них.

Решение.

Команду «зачеркни справа» нельзя применить к однозначному исходному числу. Поэтому первой будет команда «возведи в квадрат» .

Получим число 25, к которому можно применить команду «зачеркни справа» . Получим число 2.

Рассуждая аналогично, запишем команды алгоритма получения из числа 5 числа 1.

2. возведи в квадрат 5 2 = 25

1. зачеркни справа 2 5 = 2

2. возведи в квадрат 2 2 = 4

2. возведи в квадрат 4 2 = 16

1. зачеркни справа 1 6 = 1

Запишем алгоритм из номеров команд: 21221.

Ответ: 21221.

5-4

У исполнителя Вычислитель две команды, которым присвоены номера:

1. возведи в квадрат

2. прибавь b

( b – неизвестное натуральное число)

Первая из них возводит число на экране во вторую степень, вторая прибавляет к числу b .

Программа для исполнителя – это последовательность номеров команд.

Известно, что программа 12222 переводит число 6 в число 52 . Определите значение b .

Решение.

Выполним данный алгоритм для исходного числа 6:

Решим полученное уравнение:

36 + 4 b = 52

4 b = 52 – 36

4 b = 16

b = 16 / 4

b = 4

1. возведи в квадрат 6 2 = 36

2. прибавь b 36 + b

2. прибавь b (36 + b ) + b = 36 + 2 b

2. прибавь b (36 + 2 b ) + b = 36 +3 b

2. прибавь b (36 + 3 b ) + b = 36 + 4 b

При этом мы получили число 52, то есть 36 + 4 b = 52.

Ответ: 4.

2 ) Первая из них увеличивает число на экране в b раз, вторая увеличивает его на 1. Программа для исполнителя – это последовательность номеров команд. Известно, что программа 21212 переводит число 1 в число 56 . Определите значение b . Решение. Выполним данный алгоритм для исходного числа 1: Решим полученное квадратное уравнение:   2 b 2 + b – 55 = 0 D = 1 2 – 4 ∙ 2 ∙ (–55) = 441 b 1 = (–1 + 21) / 4 = 5 b 2 = (–1 – 21) / 4 = –5,5 2. прибавь 1 1 + 1= 2 1. умножь на b 2∙ b 2. прибавь 1 2 b + 1 1. умножь на b (2 b + 1) ∙ b = 2 b 2 + b 2. прибавь 1 (2 b 2 + b ) + 1 = 2 b 2 + b + 1 Так как b – натуральное число, то нам подходит только b = 5. При этом мы получили число 56, то есть 2 b 2 + b + 1 = 56. Ответ: 5. " width="640"

5-5

У исполнителя Вычислитель две команды, которым присвоены номера:

1. умножь на b

2. прибавь 1

( b – неизвестное натуральное число; b 2 )

Первая из них увеличивает число на экране в b раз, вторая увеличивает его на 1.

Программа для исполнителя – это последовательность номеров команд.

Известно, что программа 21212 переводит число 1 в число 56 . Определите значение b .

Решение.

Выполним данный алгоритм для исходного числа 1:

Решим полученное квадратное уравнение:

2 b 2 + b – 55 = 0

D = 1 2 – 4 ∙ 2 ∙ (–55) = 441

b 1 = (–1 + 21) / 4 = 5

b 2 = (–1 – 21) / 4 = –5,5

2. прибавь 1 1 + 1= 2

1. умножь на b 2∙ b

2. прибавь 1 2 b + 1

1. умножь на b (2 b + 1) ∙ b = 2 b 2 + b

2. прибавь 1 (2 b 2 + b ) + 1 = 2 b 2 + b + 1

Так как b – натуральное число, то нам подходит только b = 5.

При этом мы получили число 56, то есть 2 b 2 + b + 1 = 56.

Ответ: 5.

2 ) Первая из них увеличивает число на экране в b раз, вторая увеличивает его на 1. Программа для исполнителя – это последовательность номеров команд. Известно, что программа 21212 переводит число 1 в число 56 . Определите значение b . Решение. Выполним данный алгоритм для исходного числа 1: 2. прибавь 1 1 + 1= 2 Если у вас не получается решить квадратное уравнение, можно найти значение b методом подбора. 1. умножь на b 2∙ b 2. прибавь 1 2 b + 1 2 b 2 + b + 1 = 56 2 b 2 + b = 55 Перебирая последовательно значения b = 2, 3, 4, 5, находим подходящее значение: 2 ∙ 5 2 + 5 = 55 1. умножь на b (2 b + 1) ∙ b = 2 b 2 + b 2. прибавь 1 (2 b 2 + b ) + 1 = 2 b 2 + b + 1 При этом мы получили число 56, то есть 2 b 2 + b + 1 = 56. Ответ: 5. " width="640"

5-5

У исполнителя Вычислитель две команды, которым присвоены номера:

1. умножь на b

2. прибавь 1

( b – неизвестное натуральное число; b 2 )

Первая из них увеличивает число на экране в b раз, вторая увеличивает его на 1.

Программа для исполнителя – это последовательность номеров команд.

Известно, что программа 21212 переводит число 1 в число 56 . Определите значение b .

Решение.

Выполним данный алгоритм для исходного числа 1:

2. прибавь 1 1 + 1= 2

Если у вас не получается решить квадратное уравнение, можно найти значение b методом подбора.

1. умножь на b 2∙ b

2. прибавь 1 2 b + 1

2 b 2 + b + 1 = 56

2 b 2 + b = 55

Перебирая последовательно значения b = 2, 3, 4, 5, находим подходящее значение:

2 ∙ 5 2 + 5 = 55

1. умножь на b (2 b + 1) ∙ b = 2 b 2 + b

2. прибавь 1 (2 b 2 + b ) + 1 = 2 b 2 + b + 1

При этом мы получили число 56, то есть 2 b 2 + b + 1 = 56.

Ответ: 5.