Презентация к лекции: Переключательные схемы

План.

• Понятие переключательной схемы
• Простейшие переключательные схемы
• Задачи теории переключательных схем
• Автоматические переключатели
• Логические элементы и их реализация

Понятие переключательной схемы

• В вычислительных и других автоматических устройствах широко применяются электрические схемы, содержащие множество переключательных элементов: реле, выключателей и т.п.
• При разработке таких схем с успехом может использоваться аппарат алгебры логики.
• Переключательная схема — схематическое изображение некоторого устройства, состоящего из переключателей и соединяющих их проводников, а также входов и выходов, на которые подается и с которых снимается электрический сигнал.

Переключатели

Состояния переключателей

• Каждый переключатель может находится только в двух состояниях ВКЛ (ON) и ВЫКЛ (OFF).
• Т.е. состояние переключателя может быть описано одной логической переменной, принимающей два значения 0 и 1.
• Договоримся считать, что переключатель находится в состоянии 0, когда он поднят вверх, и в состоянии 1 — когда опущен вниз (нажат).
• Таким образом, некоторые выключатели будут проводить ток, когда их состояние равно 1, а некоторые — когда их состояние равно 0.

Типы переключателей

Переключатели и логические переменные

• Поставим в соответствие каждому выключателю логическую переменную, значение которой равно состоянию переключателя.
• Причем, нескольким переключателям может соответствовать одна переменная. Это означает, что эти переключатели меняют свои состояния одновременно (т.е. по сути все они представляют собой один переключатель, который замыкает и размыкает сразу несколько проводов).
• Таким образом, всей переключательной схеме соответствует набор логических переменных x1, x2, . . . , xn, значения которых полностью определяют состояния всех переключателей схемы.

Переключатели и логические переменные

• Используя введенные обозначения, сам переключатель можно не рисовать, а обозначать именем соответствующей ему логической переменной.
• Переключатели первого типа обозначаются просто именем переменной, например, x.
• Переключатели второго типа — отрицанием соответствующей переменной, например, ¬x.

Переключательная схема как логическая функция

• Всей переключательной схеме также можно поставить в соответствие одно логическое значение f , равное единице, если схема проводит ток, и равное нулю — если не проводит.
• Очевидно, что проводимость схемы определяется тем, в каких состояниях находятся ее переключатели.
• Другими словами, значение f является функцией логических переменных x1, x2, . . . , xn.
• Функцию f (x1; x2; : : : ; xn), соответствующую заданной схеме, принято называть функцией проводимости этой схемы.

Простейшие переключательные схемы

Схема проводит ток всегда, поэтому f — функция «константа единица»: f ≡ 1

Простейшие переключательные схемы

Схема не проводит ток никогда, поэтому f — функция «константа ноль»: f ≡ 0:

Простейшие переключательные схемы

Схема проводит ток, когда x = 1, и не проводит, когда x = 0, следовательно, f (x) = x:

Простейшие переключательные схемы

Схема проводит ток, когда x = 0, и не проводит, когда x = 1, следовательно, f (x) = x:

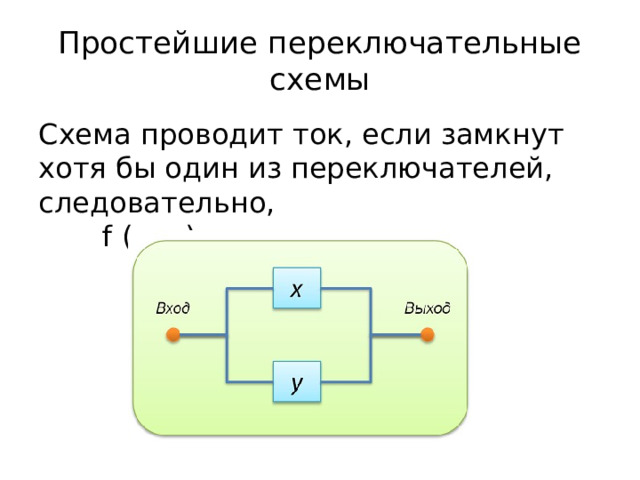
Простейшие переключательные схемы

Схема проводит ток, если замкнут хотя бы один из переключателей, следовательно, f (x; y) = x v y:

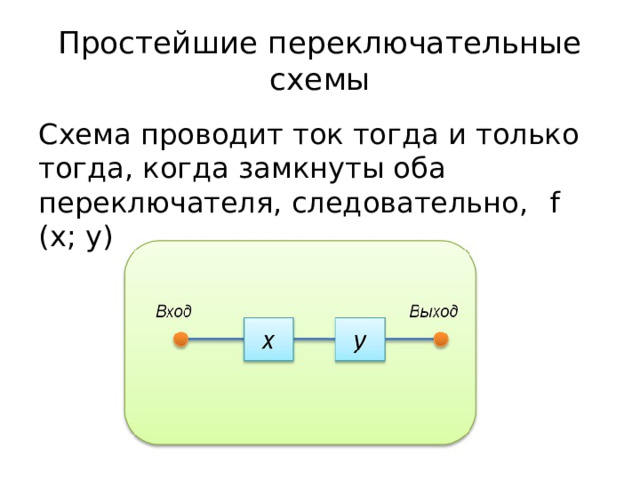
Простейшие переключательные схемы

Схема проводит ток тогда и только тогда, когда замкнуты оба переключателя, следовательно, f (x; y) = x ^ y:

Задачи теории переключательных схем

• При рассмотрении переключательных схем решают, как правило, две задачи: синтез и анализ схемы.
• Синтез переключательной схемы — это разработка схемы для заданной функции проводимости, которая в свою очередь задана либо формулой, либо таблицей истинности, либо словесным описанием.
• Анализ переключательной схемы – это построение функции проводимости для заданной схемы и возможное последующее преобразование этой функции, например, с целью ее упрощения.

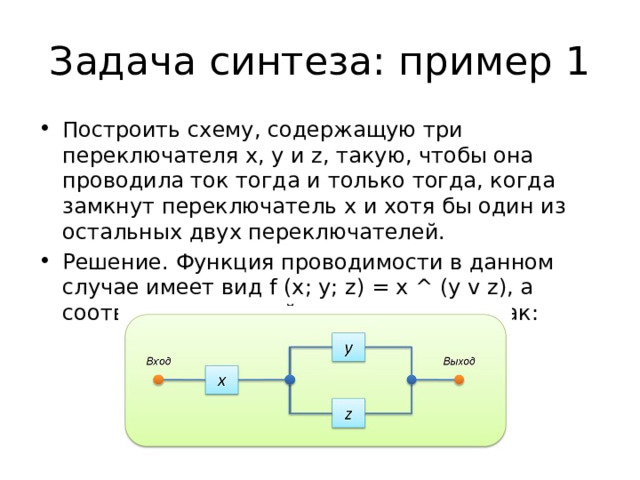
Задача синтеза: пример 1

• Построить схему, содержащую три переключателя x, y и z, такую, чтобы она проводила ток тогда и только тогда, когда замкнут переключатель x и хотя бы один из остальных двух переключателей.
• Решение. Функция проводимости в данном случае имеет вид f (x; y; z) = x ^ (y v z), а соответствующая ей схема выглядит так:

Задача синтеза: пример 1

• Построить схему, содержащую три переключателя x, y и z, такую, чтобы она проводила ток тогда и только тогда, когда замкнут переключатель x и хотя бы один из остальных двух переключателей.
• Решение. Функция проводимости в данном случае имеет вид f (x; y; z) = x ^ (y v z), а соответствующая ей схема выглядит так:

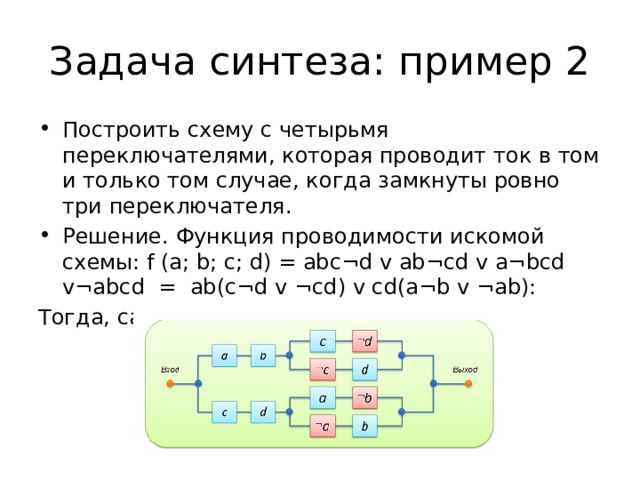
Задача синтеза: пример 2

• Построить схему с четырьмя переключателями, которая проводит ток в том и только том случае, когда замкнуты ровно три переключателя.
• Решение. Функция проводимости искомой схемы: f (a; b; c; d) = abc¬d v ab¬cd v a¬bcd v¬abcd = ab(c¬d v ¬cd) v cd(a¬b v ¬ab):

Тогда, сама схема имеет вид:

Задача синтеза: пример 2

• Построить схему с четырьмя переключателями, которая проводит ток в том и только том случае, когда замкнуты ровно три переключателя.
• Решение. Функция проводимости искомой схемы: f (a; b; c; d) = abc¬d v ab¬cd v a¬bcd v¬abcd = ab(c¬d v ¬cd) v cd(a¬b v ¬ab):

Тогда, сама схема имеет вид:

Задача синтеза: пример 3

• Построить схему с двумя переключателями, реализующую операцию строгой дизъюнкции.
• Решение. Используя таблицу истинности, построим СДНФ: x © y = x¬y v ¬xy. Исходя из полученной формулы, построим искомую схему:

Задача синтеза: пример 3

• Построить схему с двумя переключателями, реализующую операцию строгой дизъюнкции.
• Решение. Используя таблицу истинности, построим СДНФ: x © y = x¬y v ¬xy. Исходя из полученной формулы, построим искомую схему:

Задача синтеза: пример 3

• Построить схему с двумя переключателями, реализующую операцию строгой дизъюнкции.
• Решение. Используя таблицу истинности, построим СДНФ: x © y = x¬y v ¬xy. Исходя из полученной формулы, построим искомую схему:

Эта схема лежит в основе работы так называемого проходного выключателя (который может включаться-выключаться из двух разных мест).

Задача анализа: пример

• Упростить переключательную схему

• Решение. Функция проводимости данной схемы имеет вид: f (x; y) = xy v ¬yx. После очевидных упрощений получаем, что f (x; y) = x(y v ¬y) = x. Тогда, упрощенная схема выглядит следующим образом:

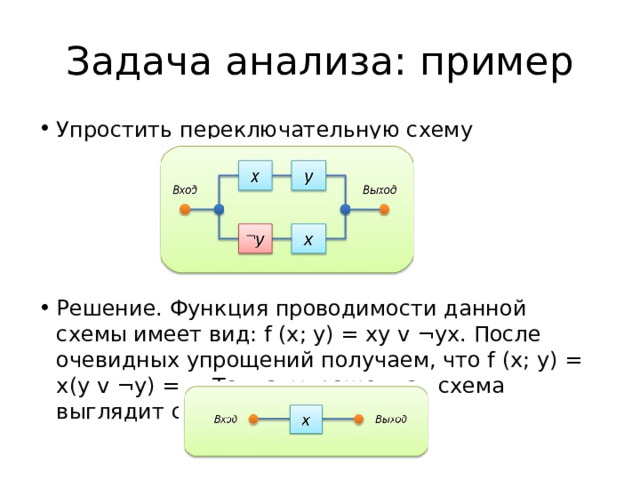
Задача анализа: пример

• Упростить переключательную схему

• Решение. Функция проводимости данной схемы имеет вид: f (x; y) = xy v ¬yx. После очевидных упрощений получаем, что f (x; y) = x(y v ¬y) = x. Тогда, упрощенная схема выглядит следующим образом:

Автоматические переключатели

• Использование переключательных схем с обычными переключателями (управляемыми вручную) неудобно, особенно если схема содержит большое количество переключателей.
• Полезными оказались переключательные схемы, в которых переключатели управляются автоматически, т.е. Под воздействием электрического тока. Если на такой переключатель подан ток, то он включен, если нет, то выключен.
• В таких схемах выходы одних переключателей могут служить управляющими входами для других переключателей, что позволяет относительно легко реализовывать сложные логические схемы.

Реле

• Исторически первыми автоматическими переключателями были телеграфные реле.
• Принцип действия реле — если на управляющий вход реле подан ток, то в катушке электромагнита возникает магнитное поле, которое притягивает металлическую пластину, что приводит к замыканию цепи между питающим током и выходом; если же на управляющем входе нет тока, то релейный контакт остается незамкнутым, следовательно, и на выходе тока не будет.

Реле

• Показанное на рисунке реле реализует функцию f (x) = x, т.к. ток на выходе реле есть только тогда, когда есть ток на его входе.

Инвертер

• Для того, чтобы реализовать с помощью реле переключатель второго типа (называемый инвертером), надо присоединить выход реле к другому контакту.
• Теперь ток на выходе будет только в том случае, если нет тока на входе, т.е. такое реле реализует логическую функцию f (x) = x.

Электронные лампы и транзисторы

• Первые электромеханические компьютеры были как раз релейными.
• На смену реле достаточно быстро пришли сначала электронные вакуумные лампы, а затем транзисторы.

Электронные лампы и транзисторы

• База транзистора является его управляющим входом, подача тока на нее «открывает» транзистор, т.е. пропускает ток с питающего входа (коллектор) на выход (эмиттер).

Компьютеры на электронных лампах

Компьютер ENIAC — первый электронный универсальный компьютер (1946 г.)

Релейные компьютеры

• Компьютер Z1 Конрада Цузе (1938 г.)

Логические элементы

• Использование автоматических переключателей дает возможность строить из них простые схемы, которые реализуют разные стандартные логические функции.
• Логический элемент (вентиль) — переключательная схема, выход которой является некоторой стандартной логической функцией от ее входов.
• Обычно логические элементы реализуют унарные (один аргумент) и бинарные (два аргумента) функции. А уже из таких элементов можно собирать более сложные логические схемы.
• Например, рассмотренные выше два типа реле представляют собой два логических элемента, реализующих функции f (x) = x и f (x) = ¬x.

Реализация логических операций: дизъюнкция

• Из двух реле можно собрать логический элемент, который будет реализовывать логическую функцию — дизъюнкцию.
• Для этого выходы этих реле надо соединить параллельно в один общий выход. Таким образом, ток на выходе элемента будет только тогда, когда есть ток хотя бы на одном его входе.

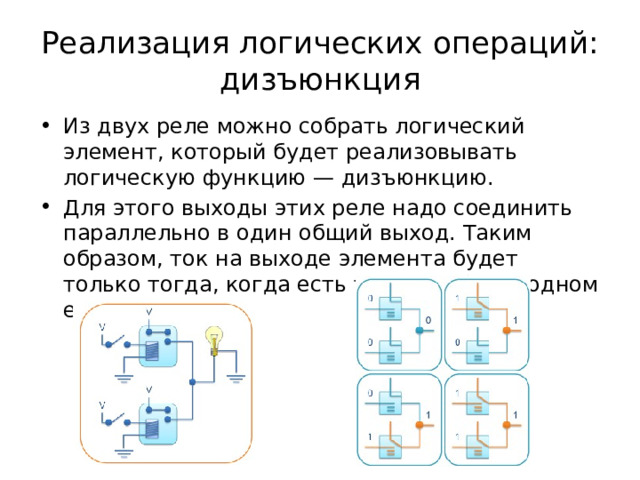
Реализация логических операций: дизъюнкция

• Из двух реле можно собрать логический элемент, который будет реализовывать логическую функцию — дизъюнкцию.
• Для этого выходы этих реле надо соединить параллельно в один общий выход. Таким образом, ток на выходе элемента будет только тогда, когда есть ток хотя бы на одном его входе.

Реализация логических операций: конъюнкция

• Похожим образом из двух реле можно собрать логический элемент, реализующий конъюнкцию.
• Для этого выход одного реле надо соединить с питающим входом другого реле. Выход второго реле будет выходом всего элемента. Таким образом, ток на выходе будет только тогда, когда есть ток на обоих его входах.

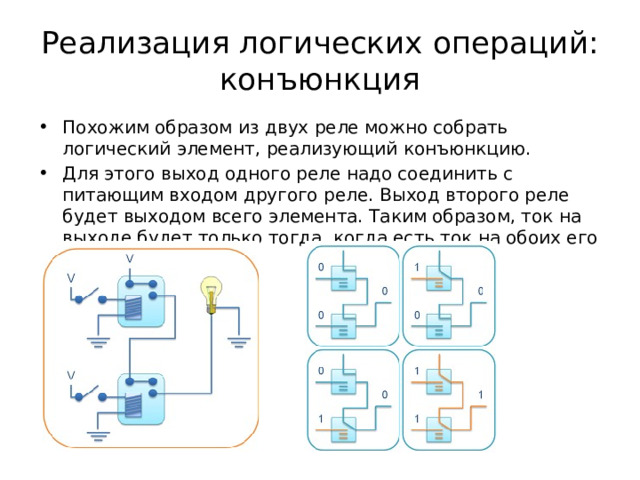
Реализация логических операций: конъюнкция

• Похожим образом из двух реле можно собрать логический элемент, реализующий конъюнкцию.
• Для этого выход одного реле надо соединить с питающим входом другого реле. Выход второго реле будет выходом всего элемента. Таким образом, ток на выходе будет только тогда, когда есть ток на обоих его входах.

Реализация логических операций: импликация

• Используя инвертер в качестве одного или обоих реле, можно построить еще несколько логических элементов.
• Например, элемент, реализующий импликацию, строится следующим образом.

Реализация логических операций: импликация

• Используя инвертер в качестве одного или обоих реле, можно построить еще несколько логических элементов.
• Например, элемент, реализующий импликацию, строится следующим образом.

Реализация логических операций: штрих Шеффера

• Соединив последовательно два инвертера, получим логический элемент, реализующий еще одну логическую функцию — штрих Шеффера f (x; y) = x | y.

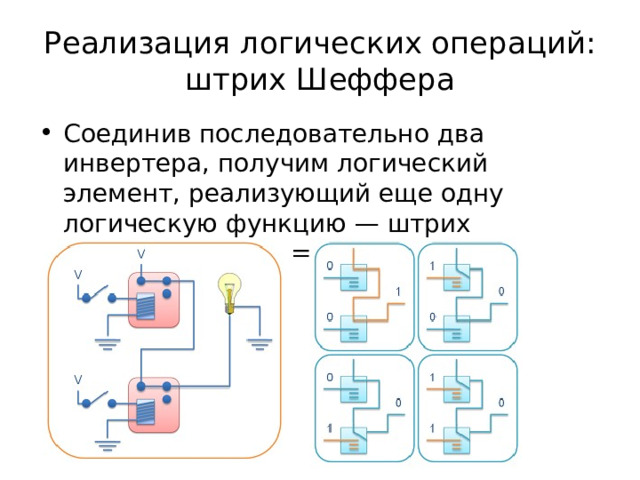
Реализация логических операций: штрих Шеффера

• Соединив последовательно два инвертера, получим логический элемент, реализующий еще одну логическую функцию — штрих Шеффера f (x; y) = x | y.

Обозначения логических элементов

• Схематически логические элементы изображаются простыми фигурами (например, в стандарте IEC прямоугольниками), имеющими несколько входов и один выход.
• Питающий вход обычно не изображается, но всегда подразумевается.
• Заметим, что обычно в построении логических схем элемент f (x) = ¬x не используется, инвертор изображается кружком, который присоединяется либо ко входу, либо к выходу некоторого другого элемента.

IEC 61131-3  — раздел международного стандарта  МЭК 61131  (также существует соответствующий европейский стандарт  EN 61131 ), описывающий языки программирования для  программируемых логических контроллеров .

Обозначения логических элементов