Презентация к работе МШНОУ по теме "Практическое применение теоремы Пифагора".

Научно – исследовательская работа по математике   «Практическое применение теоремы Пифагора»

Выполнили:

Перепёлкина Алёна, ученицы 8 класса

МАОУ СШ №10 г. Володарска

Актуальность :

«Геометрия владеет двумя сокровищами – теоремой Пифагора и золотым сечением, и если первое из них можно сравнить с мерой золота, то второе – с драгоценным камнем…».

Иоганн Кеплер

АВ 2 = АС 2 +ВС 2

Результаты анкетирования

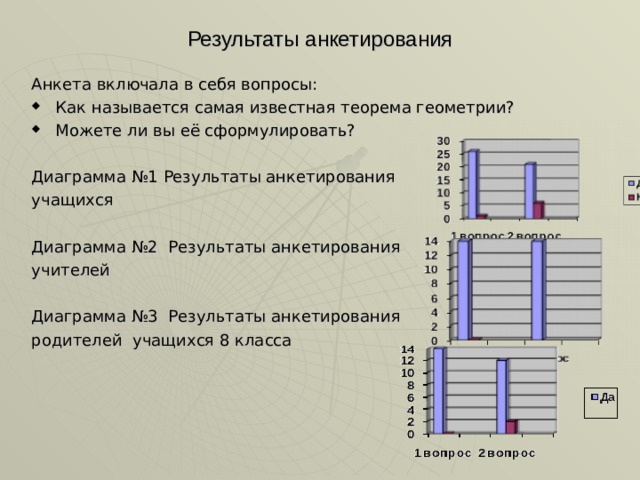
Анкета включала в себя вопросы:

• Как называется самая известная теорема геометрии?
• Можете ли вы её сформулировать?

Диаграмма №1 Результаты анкетирования

учащихся

Диаграмма №2 Результаты анкетирования

учителей

Диаграмма №3 Результаты анкетирования

родителей учащихся 8 класса

• К сожалению, в школьном курсе геометрии вопрос о практическом применении теоремы Пифагора не рассматривается.

Изучая дополнительную литературу по выбранной теме, мы выдвину ли гипотез у :

• За красоту и гармонию в природе «отвечает» математика. То есть особые числовые закономерности существуют во всем, что нас окружает.
• С помощью теоремы Пифагора можно решать не только математические задачи. Подобные задачи на вычисление стороны прямоугольных треугольников по известным сторонам решаются и в нашей повседневной жизни.

Цели и задачи:

• Изучить некоторые исторические сведения

о Пифагоре и о его теореме.

• Собрать информацию о практическом применении теоремы Пифагора в различных источниках и определить области применения теоремы.
• Показать применение теоремы при решении исторических задач.
• исследовать крышу детского сада, решить прикладные задачи по установке ёлки и молниеотвода.

А что мы знаем о Пифагоре? Чем знаменит Пифагор?

Великий ученый Пифагор родился около

570 г. до н.э. на острове Самос (откуда и

пошло прозвище Пифагор Самосский).

Пифагор – самая загадочная личность, человек-символ, философ, пророк.

Пифагор – едва ли не самый

популярный ученый за всю

историю человечества.

История открытия

теоремы Пифагора

Долгое время считали, что до Пифагора эта теорема не была известна, и поэтому ее назвали «теоремой Пифагора ».

Однако, известно, что она применялась для решения различных задач задолго до Пифагора древними египтянами, вавилонянами, китайцами, индусами и другими древними народами.

Построение прямоугольных треугольников

Египтяне строили прямоугольный

треугольник с помощью верёвки.

Этот способ легко можно воспроизвести

В архитектуре средних веков египетский треугольник применялся для построения

схем пропорциональности.

Вот что у нас вышло…

• Мы как Египтяне построили прямоугольный треугольник имея веревку и дощечку!

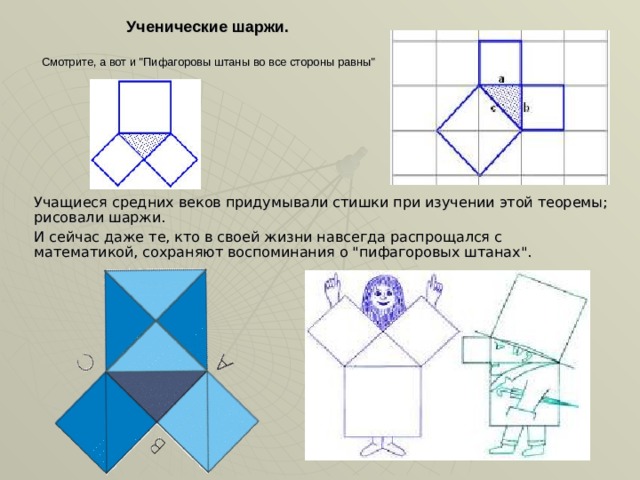
Ученические шаржи. Смотрите, а вот и "Пифагоровы штаны во все стороны равны"

Учащиеся средних веков придумывали стишки при изучении этой теоремы; рисовали шаржи.

И сейчас даже те, кто в своей жизни навсегда распрощался с математикой, сохраняют воспоминания о "пифагоровых штанах".

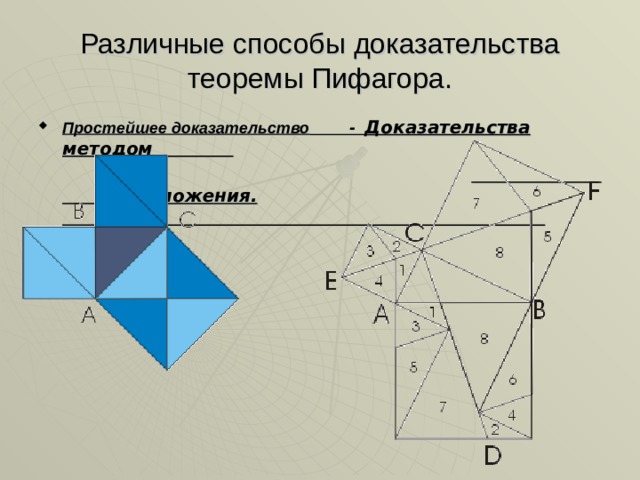
Различные способы доказательства теоремы Пифагора.

• Простейшее доказательство - Доказательства методом

разложения.

• Доказательство Нильсена.

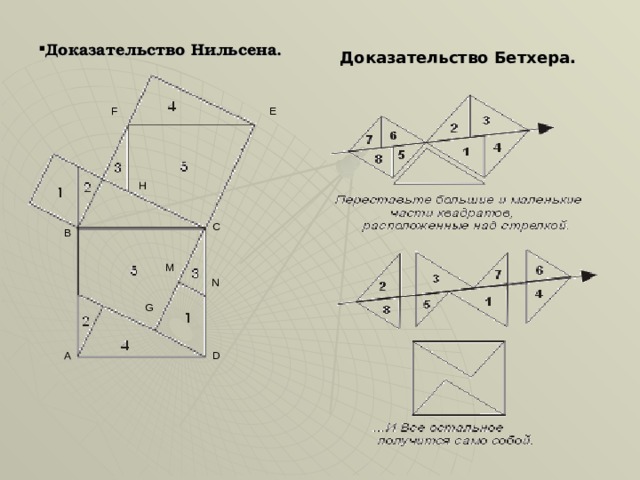
Доказательство Бетхера.

E

F

H

С

В

M

N

G

А

D

• Доказательство методом дополнения.

Доказательство методом вычитания .

От двух равных площадей нужно отнять равновеликие части так, чтобы в одном случае остались два квадрата, построенные на катетах, а в другом- квадрат, построенный на гипотенузе.

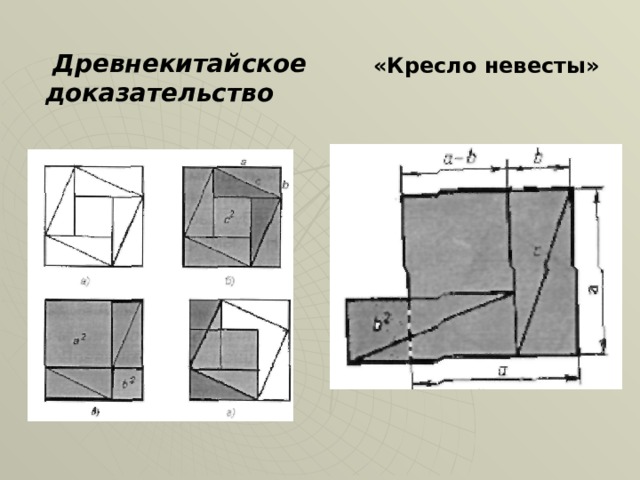
Древнекитайское доказательство

«Кресло невесты»

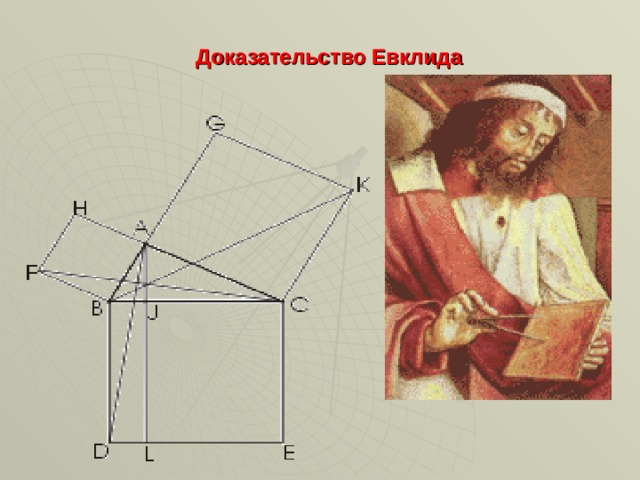
Доказательство Евклида

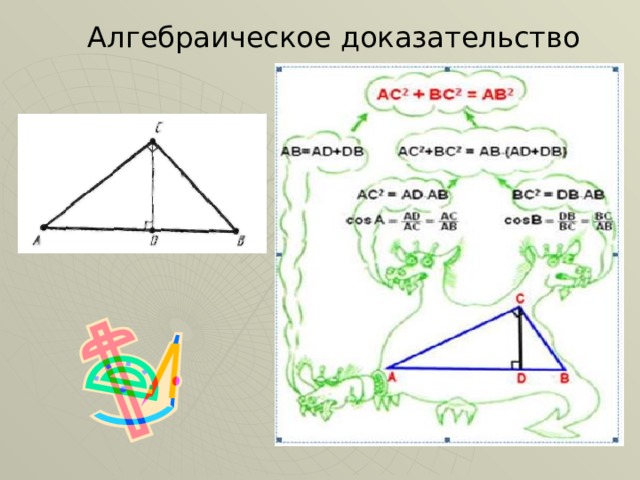
Алгебраическое доказательство

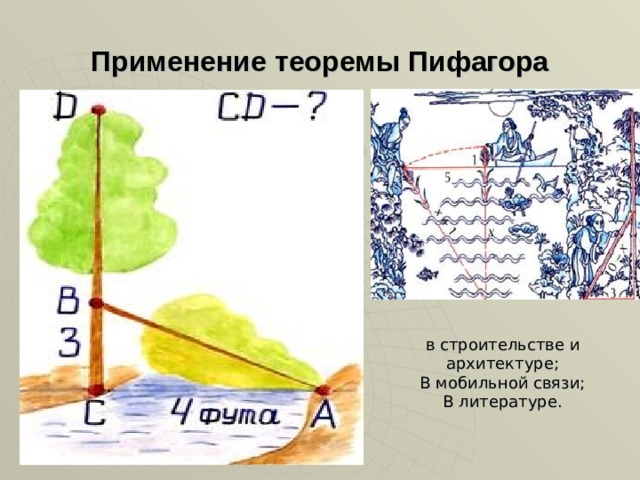
Применение теоремы Пифагора

в строительстве и архитектуре;

В мобильной связи;

В литературе.

Установка новогодней ёлки

Мы предлагаем устанавливать ёлку без снежной призмы

высотой 8м. и закрепить её в вертикальном положении.

Для этого от вершины ёлки надо сделать проволочные

натяжки АВ, АМ, АК одинаковой длины и закрепить

на земле на расстоянии 6м от основания елки.

Длина натягивающей проволоки

должна быть 10м., т.к.

по теореме Пифагора :

АВ 2 = АС 2 +ВС 2 ;

АВ=10 м.

Строительство крыши

При строительстве домов и коттеджей часто встает вопрос о длине стропил для крыши, если уже изготовлены балки.

Мы исследовали двускатную крышу

детского сада «Цыплёнок» в городе Володарске

и проверили ,выполняется ли для неё теорема

Пифагора.

Проведя измерения крыши, получили

следующие результаты:

длина балки АС = 12,2 м., высота В F =3 м.,

длина стропила А F = 6,8м.

Двускатная крыша в сечении –

равнобедренный треугольник, тогда

длину стропила вычисляем по теореме Пифагора:

А F 2 =AB 2 + BF 2

AF= √6,1 2 +3 2 ≈6,8м.

Вышка мобильной связи

При строительстве вышки (антенны) часто приходится решать

• Задачу: Какую наименьшую высоту должна иметь вышка мобильной связи, поставленная в селе Мячково, чтобы посёлок Ильино попал в зону связи (расстояние от вышки до Ильино по прямой 10 км.)?
• Решение:

Пусть AB= x – высота антенны, BC=R=10 км – радиус антенны,

OC= r =6380 км – радиус земли. OB = OA + AB OB = r + x Применив теорему Пифагора,

получили уравнение

(х+6380) 2 =10 2 +6380 2 ;

х 2 +12760х-100=0;

D =162817600+400=162818000;

D ≈12760,016;

х≈0,008км.

• Ответ: высота антенны - ≈ 8м.

Заключение

• Главным в работе считаем предложения по решению выдвинутых нами двух проблем: возведение молниеотвода на крыше детского сада и установке новогодней ёлки.
• В результате решения поставленных задач мы пришли к выводу, что выдвинутая гипотеза нашла подтверждение. Да, действительно, с помощью теоремы Пифагора можно решать не только математические задачи.

Теорема Пифагора нашла своё применение в строительстве и архитектуре, мобильной связи, литературе.

Если дан нам треугольник И притом с прямым углом, То квадрат гипотенузы Мы всегда легко найдём: Катеты в квадрат возводим, Сумму степеней находим И таким простым путём К результату мы придём.